
Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
Reading time: 40 minutes | Coding time: 20 minutes
A Rope data structure is a tree data structure which is used to store or manipulate large strings in a more efficient manner. It allows for operations like insertion, deletion, search and random access to be executed faster and much more efficiently in comparison to a traditional String. We will look into this data structure and its various operations and implementation.
This data structure is widely used by softwares such as text editors like Sublime, email systems like Gmail and text buffers to handle large strings efficiently.
Introduction
A rope is a type of binary tree i.e. each node can have maximum of 2 children at the maximum, where every leaf node holds a String or a Substring and the length of the same(Also known as the "weight" for the corresponding leaf node) and every following parent node holds the total sum of the weights of the leaf nodes in its left subtree, which in turn is described as the weight of the said node. In a more simpler form, the weight of a node is the sum of all the leaf nodes that sprout from its immediate left child node.
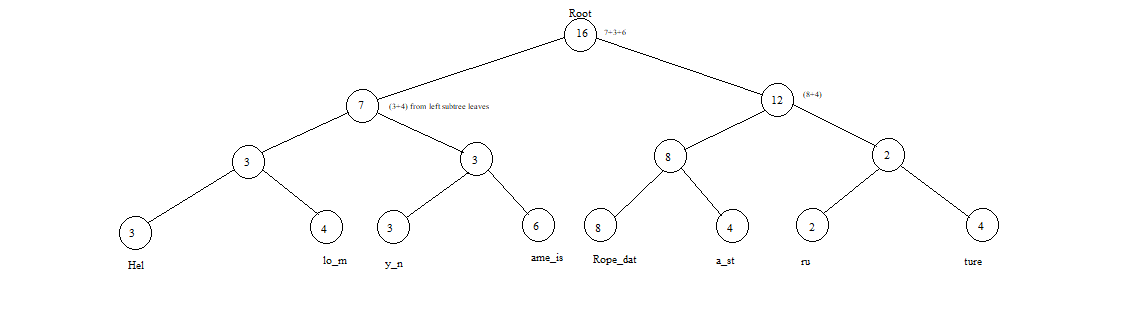
In this article we will understand the Rope Data Structure along with its comparison to a standard string to determine when or when not to use it, along with its advantages & disadvantages. There is a wide variety of applications for the Rope, however the most common is found in text editors which handle large amounts of text.
Rope Data Structure
A rope is made up of nodes, arranged into a binary tree. As a tree, its starting node is marked as the Root and has a left & right child node which further have their child nodes and those with no children are known as leaf nodes. If we take the number of levels to be h, where h=0 for the root, the maximum possible nodes in a rope can be 2(h+1)-1.
Before diving into the implementation, let us compare this data structure with a string:
Comparison with String
Advantages
- Ropes enable much faster insertion and deletion of text in comparison to string arrays, on which the operations have a time complexity of O(n).
- Ropes do not require O(n) extra memory when being operated upon, unlike arrays which require it for copying operations.
- Ropes do not need large contiguous memory areas like arrays.
- If the operations performed are non-destructive(i.e the altered content is preserved) it behaves as a persistent data structure allows for multiple undo levels.
- Stable performance regardless of size.
Disadvantages
- Occupies greater overall storage space in comparison to a simple string, when not being operated upon, in order to store the parent nodes. However, this trade-off reduces as the string grows.
- Increased complexity of structure creates a greater risk of bugs.
- Significantly slower on small strings.
From this, we can derive that ropes are more preferable when the size of our data is large and it is to be modified on a regular basis. Strings perform better on smaller data & are better when there are less operations.
Operations
Search(Index I)
In order to find the character at ith position, we search recursively beginning at the root node.
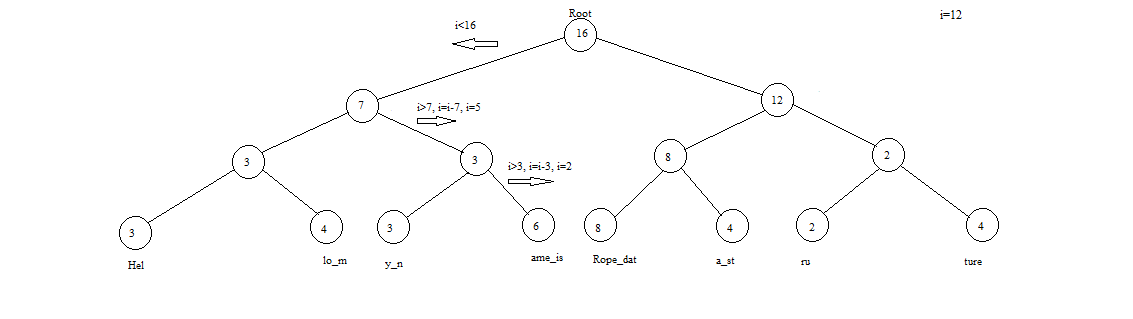
We follow the premise that if the weight of the current node is lower than the value of i, we subtract the weight from i & move right. If the weight is less than value of i we simply move left. We continue till the point we reach a leaf node.
function index(RopeNode node, integer i)
if node.weight < i and exists(node.right) then
return index(node.right, i - node.weight)
end
if exists(node.left) then
return index(node.left, i)
end
return node.[i]string
end
Average case Time complexity: Θ(N)
Average case Time complexity: Θ(log n)
Concatenation(S1+S2)
A concatenation operation between 2 strings(S1 & S2) is performed by creation of a new root node which has a weight equal to the sum of weights of leaf nodes in S1. This takes time if the tree is already balanced. Since, most of the rope operations need a balanced tree, it might require re-balancing after the operation.
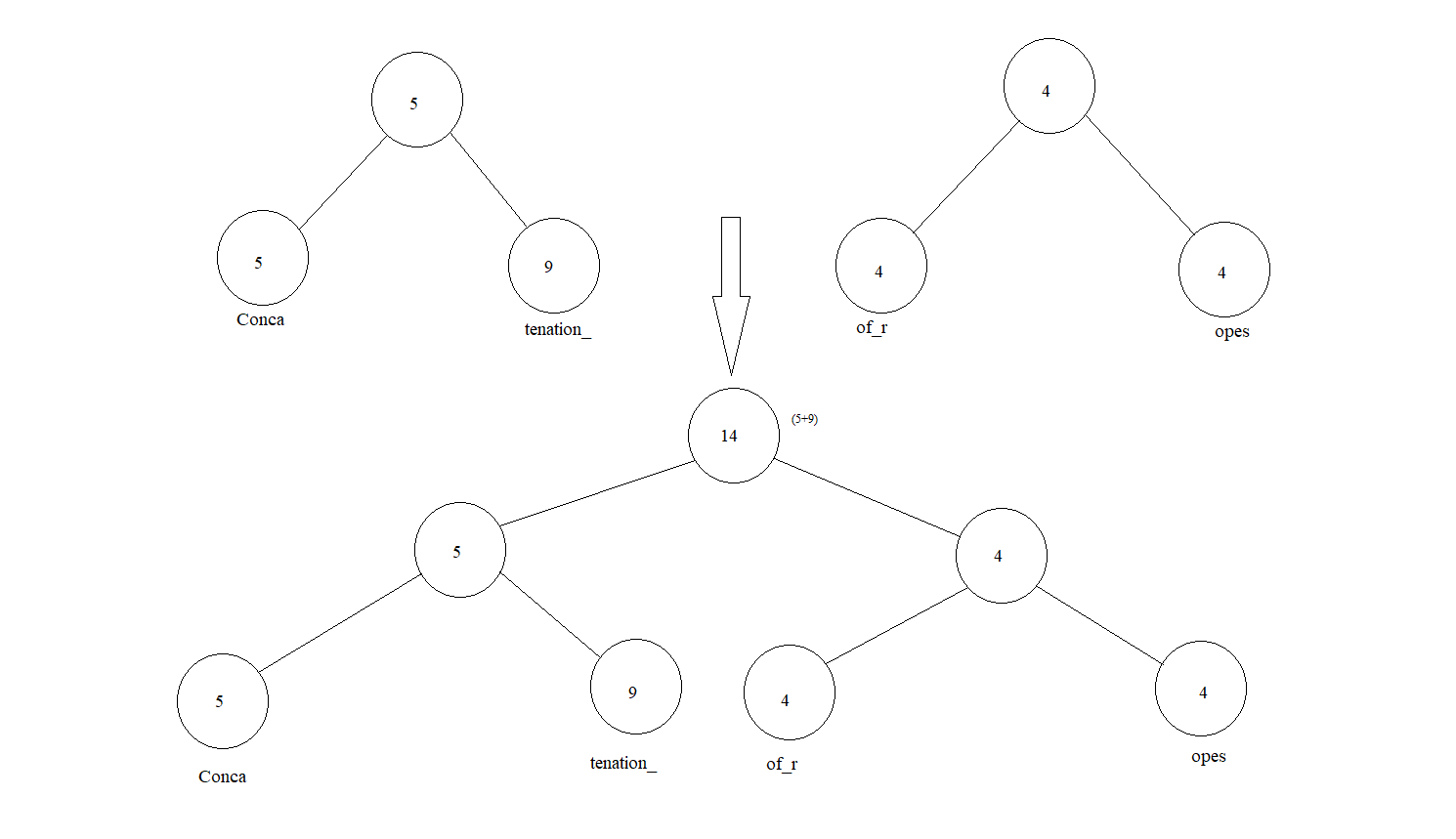
function concatenation(ropenode node1, ropenode node2)
newrope.left = node1
newrope.right = node2
newrope.val = length(node1)
Time complexity: Θ(1) to concatenate strings and Θ(log N) to calculate weight of root.
Split(I)
In order to split a string at any given point i, there are 2 major cases we might encounter:
- Split point being the last character of a leaf node.
- Split point being a middle character of a leaf node.
With the second case, we can reduce it to the much simpler first one by splitting the string at given point into 2 leaf nodes & creating a new parent for these component strings. Follow this with subtracting the weights of the cut off parts from the parent nodes and re-balancing the tree.
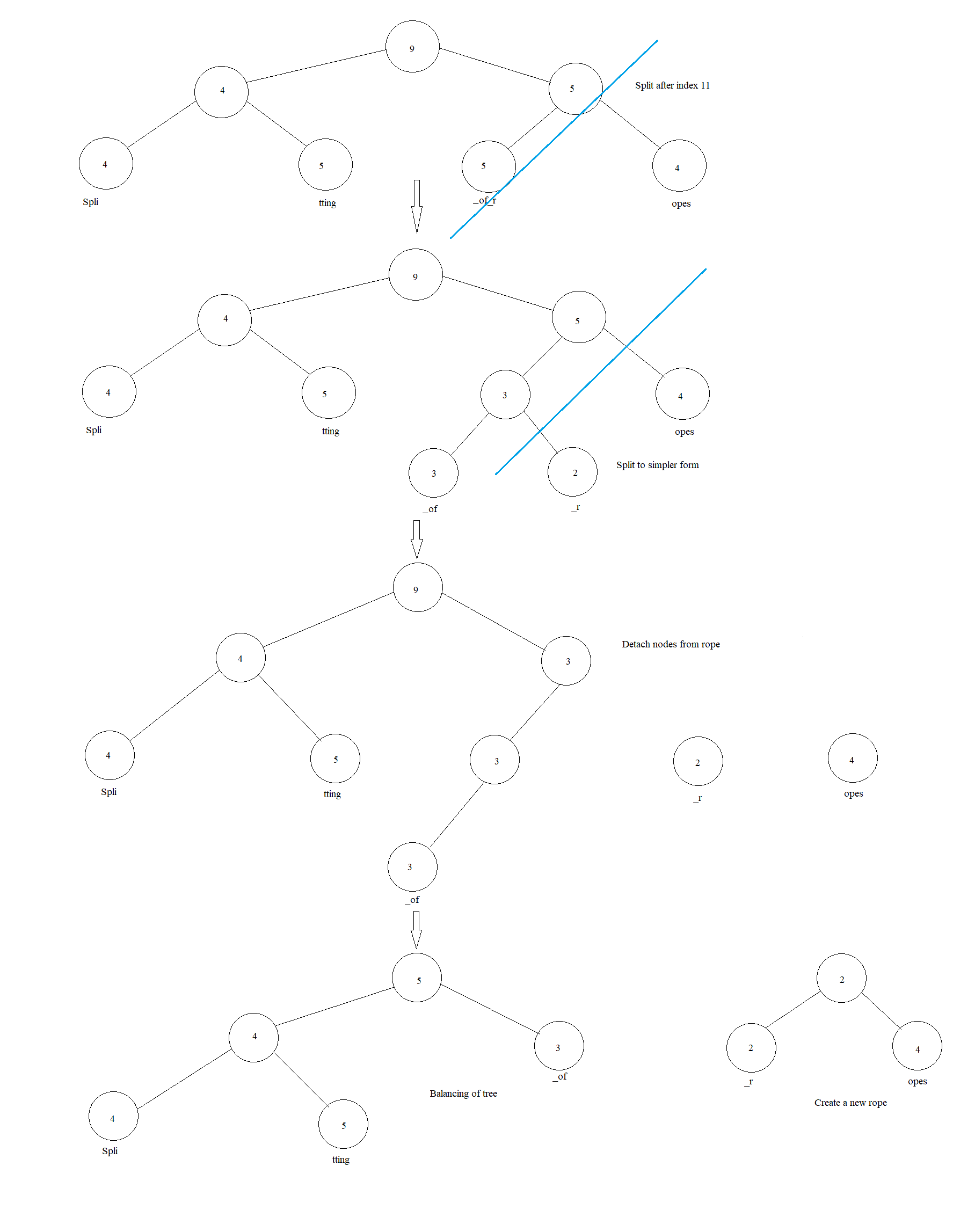
Time complexity: Θ(log N)
Insertion(I,S')
In order to insert a string S' between our string, at position i, we simply need to split it at the index from which to insert, and the concatenate the new string followed by the split off part of the original string. The cost of this operation is the sum of the three operations performed.
function insert(index i, string S')
newrope = split(i)
concatenation(S',newrope)
concatenation(rope,S')
Time complexity: Θ(log N)
Deletion(I,J)
In order to delete a part of string from the middle, split the string at provided indices from ith to i+jth character and then concatenate the strings without the remaining part.
function delete(index i, index j)
splitrope = split(j)
remove = split(i)
concatenation(rope,splitrope)
Time complexity: Θ(log N)
Report(I,J)
In order to report the string between given points, find the node that contains the starting character and whose weight is greater than the ending index j. Then traverse the tree starting at this node and output all the characters by performing an in-order traversal operation.
Time complexity: Θ(j + log N)
Implementation
Implementation of a Rope from a provided string:
class Rope(object):
#Accepts a string or list of strings and forms it into a rope.
#This is the basic implementation which forms a rope with the input data.
#Create an object and pass the string or list as the argument to the constructor to form a rope.
#Ex - s= Rope('abcxyz') or s = Rope(['abc','def','ghi'])
#Simply use print on the instance of this class in order to print the entire string. Ex - print(s)
def __init__(self, data=''):
#check if the input data is string or not
if isinstance(data, list):
if len(data) == 0:
self.__init__()
elif len(data) == 1:
self.__init__(data[0])
else:
# Round-up division (to match rope arithmetic associativity)
idiv = len(data) // 2 + (len(data) % 2 > 0)
self.left = Rope(data[:idiv])
self.right = Rope(data[idiv:])
self.data = ''
self.length = self.left.length + self.right.length
elif isinstance(data, str):
self.left = None
self.right = None
self.data = data
self.length = len(data)
else:
raise TypeError('Kindly use strings for the purpose')
# Word iteration
self.current = self
#checks if the tree is balanced
def __eq__(self, other):
if (self.left and self.right) and (other.left and other.right):
return self.left == other.left and self.right == other.right
elif (self.left and self.right) or (other.left and other.right):
return False
else:
return self.data == other.data
#concatenation of strings
#forms a new rope with other string and joins the 2 ropes
#into a new rope
def __add__(self, other):
#ensure that the string being concatenated is of type string
if isinstance(other, str):
other = Rope(other)
r = Rope()
r.left = self
r.right = other
r.length = self.length + other.length
r.current = self
return r
#Fetch the length of string in the specified rope
def __len__(self):
if self.left and self.right:
return len(self.left.data) + len(self.right.data)
else:
return(len(self.data))
#fetch the word present at the specified index
def __getitem__(self, index):
#ensure the index specified is an integer
if isinstance(index, int):
if self.left and self.right:
if index < -self.right.length:
subindex = index + self.right.length
elif index >= self.left.length:
subindex = index - self.left.length
else:
subindex = index
if index < -self.right.length or 0 <= index < self.left.length:
return self.left[subindex]
else:
return self.right[subindex]
else:
return Rope(self.data[index])
elif isinstance(index, slice):
if self.left and self.right:
start = index.start
if index.start is None:
if index.step is None or index.step > 0:
head = self.left
else:
head = self.right
elif (index.start < -self.right.length or
0 <= index.start < self.left.length):
head = self.left
if index.start and index.start < -self.right.length:
start += self.right.length
else:
head = self.right
if index.start and index.start >= self.left.length:
start -= self.left.length
stop = index.stop
if index.step is None or index.step > 0:
if (index.stop is None or
-self.right.length <= index.stop < 0 or
index.stop > self.left.length):
tail = self.right
if index.stop and index.stop > self.left.length:
stop -= self.left.length
else:
if head == self.right:
tail = self.right
stop = 0
else:
tail = self.left
if index.stop < -self.right.length:
stop += self.right.length
else:
if (index.stop is None or
index.stop < (-self.right.length - 1) or
0 <= index.stop < self.left.length):
tail = self.left
if index.stop and index.stop < (-self.right.length - 1):
stop += self.right.length
else:
if head == self.left:
tail = self.left
stop = -1 # Or self.left.length - 1 ?
else:
tail = self.right
if index.stop >= self.left.length:
stop -= self.left.length
# Construct the rope as a binary tree
if head == tail:
return head[start:stop:index.step]
else:
if not index.step:
offset = None
elif index.step > 0:
if start is None:
delta = -head.length
elif start >= 0:
delta = start - head.length
else:
delta = max(index.start, -self.length) + tail.length
offset = delta % index.step
if offset == 0:
offset = None
else:
if start is None:
offset = index.step + (head.length - 1) % (-index.step)
elif start >= 0:
offset = index.step + min(start, head.length - 1) % (-index.step)
else:
offset = index.step + (start + head.length) % (-index.step)
if not tail[offset:stop:index.step]:
return head[start::index.step]
else:
return head[start::index.step] + tail[offset:stop:index.step]
else:
return Rope(self.data[index])
#Report the characters present inside the rope
def __repr__(self):
if self.left and self.right:
return '{}{} + {}{}'.format('(' if self.left else '',
self.left.__repr__(),
self.right.__repr__(),
')' if self.right else '')
else:
return "Rope('{}')".format(self.data)
#Check if the current node is a leaf node and print its value
#otherwise iterate down a step on both sides
def __str__(self):
if self.left and self.right:
return self.left.__str__() + self.right.__str__()
else:
return self.data
#The iterator
def __iter__(self):
return self
#Iteration down the tree
def __next__(self):
if self.current:
if self.left and self.right:
try:
return next(self.left)
except StopIteration:
self.current = self.right
return next(self.right)
else:
self.current = None
return self.data
else:
raise StopIteration
def next(self):
return self.__next__()
firstRope = Rope('hello_my_name_is')
secondRope = Rope('_rope_data_structure')
#concatenate these strings
fullRope = firstRope.__add__(secondRope)
print(fullRope)
#Gives result hello_my_name_is_rope_data_structure
#Show the character at specified index
print(fullRope.__getitem__(14))
#Displays character "i" which is at index 14
Complexity
- Worst case time complexity:
Θ(n) - Average case time complexity:
Θ(log N) - Best case time complexity:
Θ(log N) - Space complexity:
Θ(n)
Applications
The areas where the Rope data structure is used are:
- Text Editors which handle large amounts of strings.
- E-mail messages which might require lot of editing.
- Edit buffers for handling large text.
- Cedar programming environment uses ropes since its inception.
