Schedule Events in Calendar Problem [Segment Tree]

In this article, we will discuss the My Calendar 1 problem where we need to schedule events in a calendar such that there is no conflict. This will involve the concept of Segment Tree.

Pre-requisites

• Line sweep algorithm
• Segment tree

Problem statement

Here you will be given a couple of start and end time of some events. You have to return true if the event is executable and false if its not.

An event is executable if its start and end time does not overlap with other events intervals, though an event can end and start at the same time. Priorities for these events is given as per the order they are called based on FCFS, so if a particular interval is booked by an event then its fixed no one can change it.

Example:

Input
["MyCalendar", "book", "book", "book"]
[[], [10, 20], [15, 25], [20, 30]]
Output
[null, true, false, true]

Explanation
MyCalendar myCalendar = new MyCalendar();
myCalendar.book(10, 20); // return True
myCalendar.book(15, 25); // return False, It can not be booked because time 15 is already booked by another event.
myCalendar.book(20, 30); // return True, The event can be booked, as the first event takes every time less than 20, but not including 20.

Observation

From the examples we can understand that, if an events end time and an events start time is equal then that even can be executed and hence we can return true.

Approach 1

Here we will discuss how to solve this problem using line sweep algorithm.

Intuitive steps

• Create a map
• Add 1 for start in the map
• Subtract 1 for end in the map
• Initialize sum=0
• Iterate through the map
• Add key to sum
• Return false if sum>1
• Return true outside the loop

Explained

• First we will create a map<int, int> to store the occurrence of start and end timings.
• Now inside the book() first we will increment the key of start value inside the ma by 1. Then we will decrement the key of the end value inside the map by 1. So by the end of this step we have marked the start and end point of the event inside the map and all the values will be stored inside the map in an increasing order.
• Next we will initialize a variable sum which we will use to sum up the key values in the next step.
• Since we marked the starting point with 1 and the ending point by -1, we can say that when the sum is equal to 1 an event is going on, when it is 0 no event is going on and when it is 2 then the events are overlapping.
• On the basis of the above principle we iterate through the map, and for each value in the map we will add its key to the sum variable and then we will check if an overlapping is present or not.
• If overlapping is present (sum>1) we will first remove the effect of the start and end values of the given event by doing the opposite of what we did earlier. We will decrement the key of the start value and increment the key of the end value inside the map, and then return false.
• If no overlapping is found then return true outside the for loop.

The following diagram demonstrates the same.

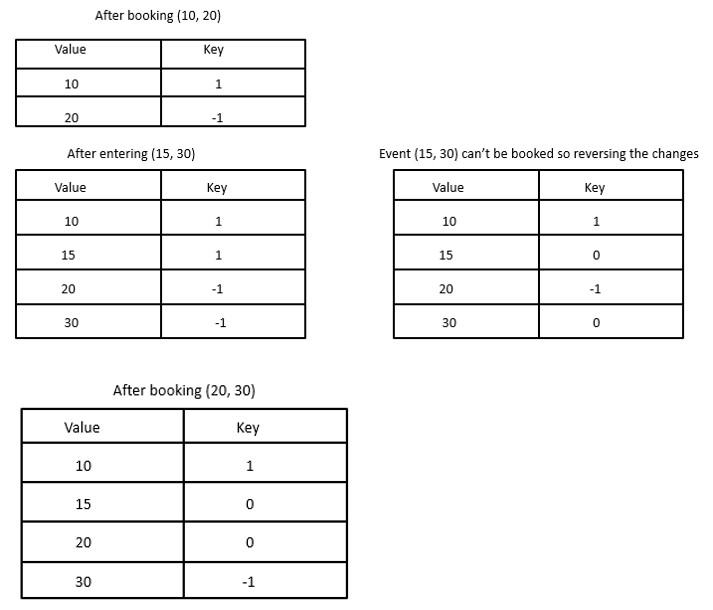
Since we are using a map, the values will be in ordered always. Hence in the table you can see that when ever the sum crosses the value 1 (when you add the keys of 10 and 15), it means that they are overlapping and it reverses the changes and the event can't be booked else its booked.

Code:

#include<bits/stdc++.h>

using namespace std;

map<int,int>mp;

 bool book(int start, int end) {
    mp[start]++;
    mp[end]--;
    int sum=0;
    for(auto it=mp.begin();it!=mp.end();it++){
        sum+=it->second;
        if(sum>1){
            mp[start]--;
            mp[end]++;
            return false;
        }
    }
    return true;
}

int main(){
    int n;
    cout<<"Enter number of events: ";
    cin>>n;
    vector<bool>ans(n);
    for(int i=0;i<n;i++){
        int start, end;
        cout<<"Enter start and end for event "<<i+1<<": ";
        cin>>start>>end;
        ans[i]=book(start,end);
    }
    cout<<"Answer: ";
    for(int i=0;i<n;i++){
        cout<<ans[i]<<" ";
    }
    return 0;
}

Complexity Analysis

The time complexity of the book function is O(n logn), where n is the total number of bookings made so far. The insertion and deletion in the map take O(logn) time, and the loop over the map takes O(n) time in the worst case (when all the bookings are consecutive and cover the entire time range). Therefore, the overall time complexity of the function is O(nlogn).

The space complexity of the book function is O(n), where n is the total number of bookings made so far. This is because the map stores the start and end times of all the bookings made so far, and the number of entries in the map is proportional to the number of bookings. Therefore, the space required by the map grows linearly with the number of bookings.

Output

Enter number of events: 3
Enter start and end for event 1: 10
20
Enter start and end for event 2: 15
25
Enter start and end for event 3: 20
30
Answer: 1 0 1

Approach 2

In this approach we will use segment trees to solve this question.

Intuitive steps

• Create a segment tree
• Call the function
• If the node is booked, return false
• If node matches the boundary, ans its not booked, mark it booked and return true
• If the current node is not the correct place then traverse to it using certain techniques.
• To traverse the right direction we can compare mid value of the current node with start and end using recursion to find appropriate location.

Explained
In this explanation we will take the input in the example to understand the solution better.

• A segment tree consisting of a single node is initialized when the MyCalendar object cal is created. At this point the tree has the range from 0 to 1e9.
• When the first call is made for 10, 20 the book() will check whether the range [10, 20) is available in the segment tree. For this first we will first find the mid using the start and end of the current node.
• Then we will check if the end<=mid.
  • If it is then we have to go to the left side.
  • To do that we will first check if there is a left node
  • If its not there we will create it and then recursively call the book() and pass in the new node / left node into the function
• Else if we will check if start>=mid
  • If it is we will do the same steps for this node, but instead of left, this time we will go right.
• Now these above steps will be continued until we reach the required node.
• So in this case our start=10 and end=20. So when we get the node with these values we will check if its already booked?
  • If it is then we will return false
  • If its not then we will mark it booked and then return true.
• The starting statement returns false when it gets a node marked booked.
• This statement will return false for the next call 15, 25 the moment it encounters the node with booked value.
• In the same way we will mark booked for the third value 20, 30.

The following is a close representation of the segment tree.

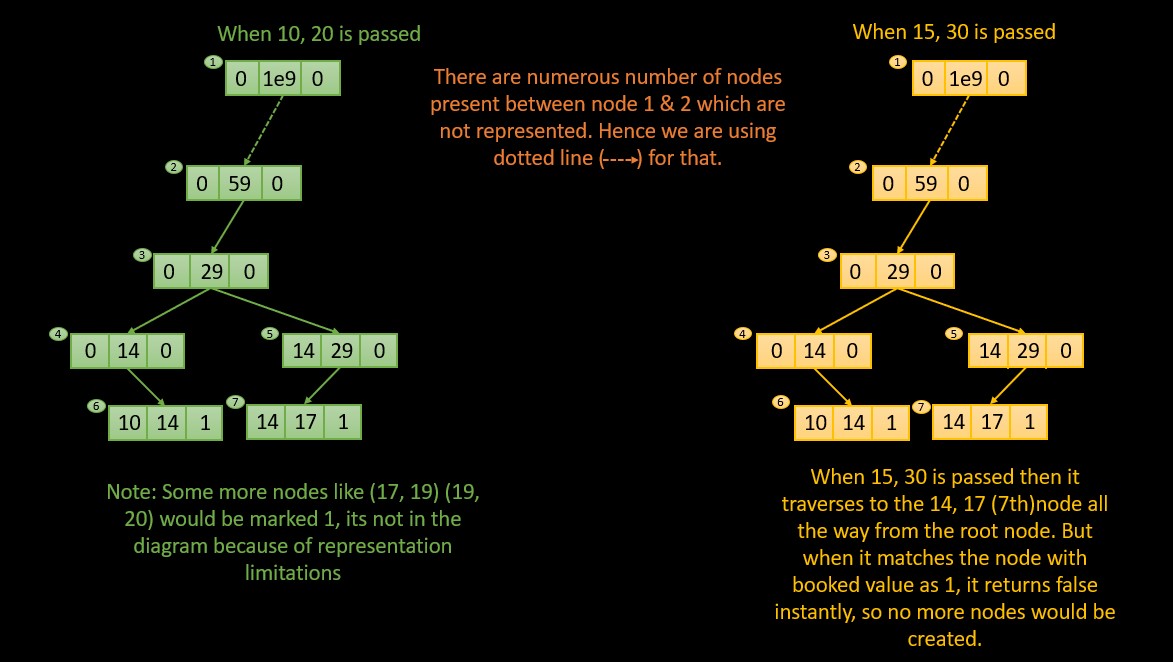
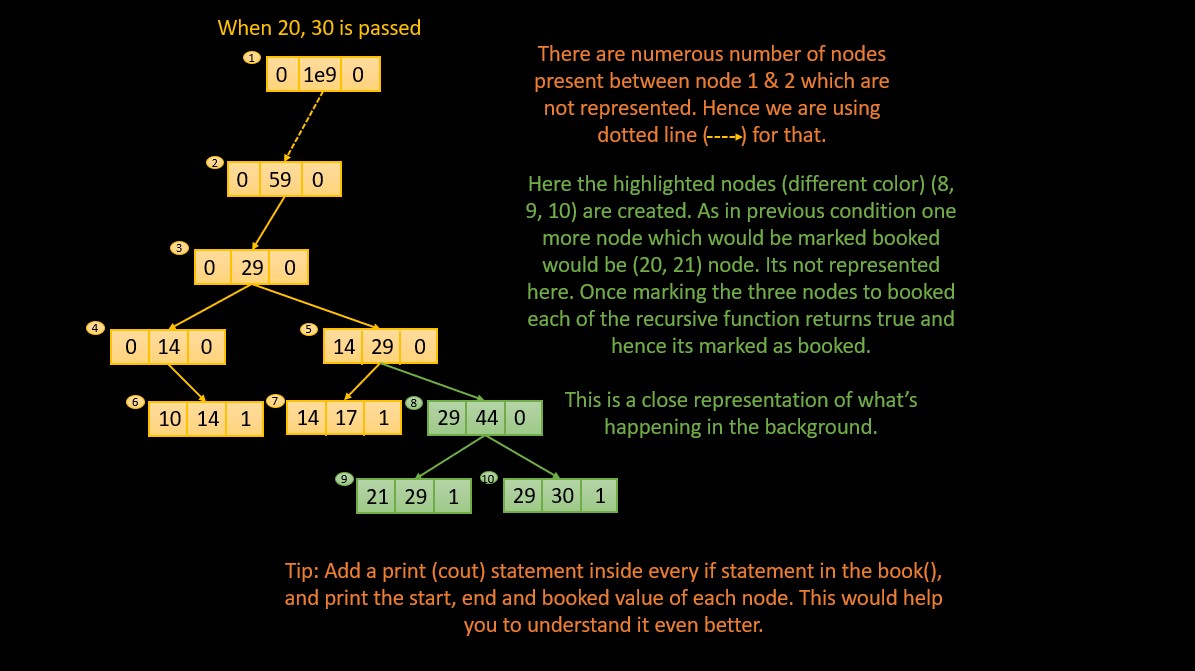
#include<bits/stdc++.h>

using namespace std;

class SegmentTreeNode {
public:
    int start, end, booked;
    SegmentTreeNode* left;
    SegmentTreeNode* right;
    SegmentTreeNode(int start, int end): start(start), end(end), booked(0), left(NULL), right(NULL) {}
};

class MyCalendar {
private:
    SegmentTreeNode* root;

    bool book(SegmentTreeNode* node, int start, int end) {
        if (node->booked > 0) {
            return false; // already booked
        }
        if (node->start == start && node->end == end) {
            node->booked = 1; // mark as booked
            return true;
        }
        int mid = node->start + (node->end - node->start) / 2;
        if (end <= mid) {
            if (!node->left) {
                node->left = new SegmentTreeNode(node->start, mid);
            }
            return book(node->left, start, end);
        } else if (start >= mid) {
            if (!node->right) {
                node->right = new SegmentTreeNode(mid, node->end);
            }
            return book(node->right, start, end);
        } else {
            if (!node->left) {
                node->left = new SegmentTreeNode(node->start, mid);
            }
            if (!node->right) {
                node->right = new SegmentTreeNode(mid, node->end);
            }
            return book(node->left, start, mid) && book(node->right, mid, end);
        }
    }

public:
    MyCalendar() {
        root = new SegmentTreeNode(0, 1e9);
    }

    bool book(int start, int end) {
        return book(root, start, end);
    }
};
int main() {
    MyCalendar cal;
    int n;
    cout<<"Enter number of events: ";
    cin>>n;
    vector<bool>ans(n);
    for(int i=0;i<n;i++){
        int start, end;
        cout<<"Enter start and end for event "<<i+1<<": ";
        cin>>start>>end;
        ans[i]=cal.book(start,end);
    }
    cout<<"Answer: ";
    for(int i=0;i<n;i++){
        cout<<ans[i]<<" ";
    }
    return 0;

    return 0;
}

Complexity Analysis

Here the time complexity of the program is O(log N), where N is the upper bound of the interval range and in this case it 1e9. This is happening because a segment tree is a binary tree with height log Nand the book() traverses the tree from root to the leaf node which will take log N steps.

The space complexity would be O(N) because the segment tree has N nodes, where N is the upper bound of the interval range. So here each node would be represented by an object of the class, which has a constant amount of memory overhead. Hence the space is proportional to O(N).

Here I have said that the space and time both depends on N, but in most of the cases the time and space would always be less than the stated complexities. This is because the tree we are creating is sparse, which means that we are not creating all possible intervals in the range [0, N). Hence the time and space complexities will we less than the stated amount.

Output

Enter number of events: 3
Enter start and end for event 1: 10
20
Enter start and end for event 2: 15
25
Enter start and end for event 3: 20
30
Answer: 1 0 1

Nodes visited

In the above diagram I mentioned that if you include a print (cout) statement then you can see all the nodes visited. The following is all the nodes in the order start, end and booked when each of the time interval booked.

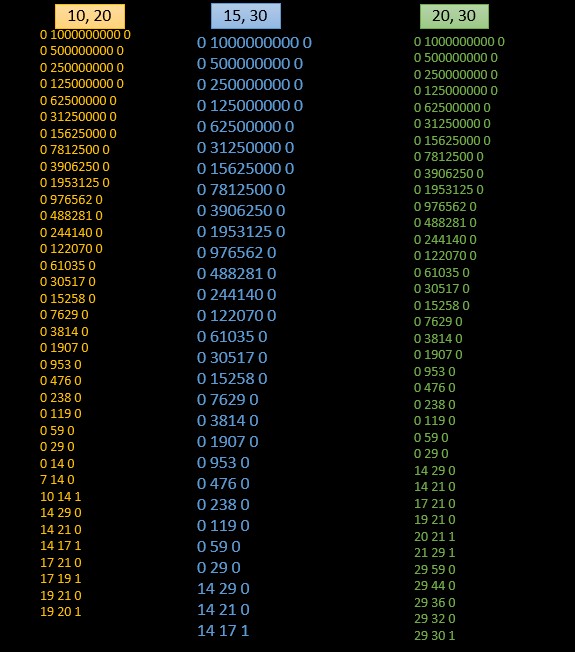
From this list identifying which node is the child of a particular parent is tough. I followed the following steps to obtain the approximate structure.

• Find the common node in all three lists with a bit high mid value.
• You can see 0, 59, 0 could be an ancestral node of many of the following nodes. So keep it in top.
• Here we are comparing the node values of children with the mid value of the parent.
  • When its smaller go left
  • else go right
• So follow these properties and then you will get an approximate image like the one you saw before.

With this article at OpenGenus, you must have the complete idea of solving this Calendar problem using Segment tree.