
Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
Given a set of numbers, partition the set or array into two subsets such that the sum of both subarrays is equal. We solved this problem using a Dynamic Programming approach.
For example, for an array of numbers A= {7, 5, 6, 11, 3, 4}
We can divide it into two subarrays in 2 ways:
{5, 6, 7} and {11, 3, 4}
{3, 4, 5, 6} and {11, 7}
The above problem can be solved by the following steps:
Assuming that the sum of all elements of the array is S, this implies that the two subsets must have an equal sum of S/2. Hence,
- Find the sum of all the elements of the array. If the sum is odd, the array cannot be partitioned into two subarrays having equal sums.
- If the sum is even, divide the array into subsets, such that both have sums equal to sum/2.
For the second step, we can use a number of different methods, as stated below:
Brute force Approach
This is a recursive method in which we consider each possible subset of the array and check if its sum is equal to total sum S/2 or not, by eliminating the last element in the array in each turn.
The algorithm for this method is:
- For each recursion of the method, divide the problem into two sub problems such that:
- Create a new subset of the array including the last element of the array if its value does not exceed S/2 and repeat the recursive step 1 again for the new subarray
- Create a new subset of the array excluding the last element of the array and repeat the recursive step 2 again for the new subarray
- If the sum of any of the above subsets is equal to S/2, return true otherwise return false
- If any of the above sub problems return true, then return true otherwise return false
The code for this method is:
#include <bits/stdc++.h>
using namespace std;
bool subset (int arr[], int n, int sum)
{
if (sum == 0)
return true;
if (n == 0 && sum != 0)
return false;
// If last element is greater than sum, then ignore it
if (arr[n-1] > sum)
return subset (arr, n-1, sum);
// check if sum can be obtained by excluding the element or including it
return subset (arr, n-1, sum) ||
subset (arr, n-1, sum-arr[n-1]);
}
bool partition (int arr[], int n)
{
int sum = 0;
for (int i = 0; i < n; i++)
sum += arr[i];
// If sum is odd, there cannot be two subsets
// with equal sum
if (sum%2 != 0)
return false;
// Find if there is subset with sum equal to
// half of total sum
return subset (arr, n, sum/2);
}
int main()
{
int arr[] = {7, 5, 6, 11, 3, 4};
int n = sizeof(arr)/sizeof(arr[0]);
if (partition(arr, n))
cout << "Can be divided into two subsets "
"of equal sum";
else
cout << "Can not be divided into two subsets"
" of equal sum";
return 0;
}
For the given example the recursive tree for the above solution will look like this:
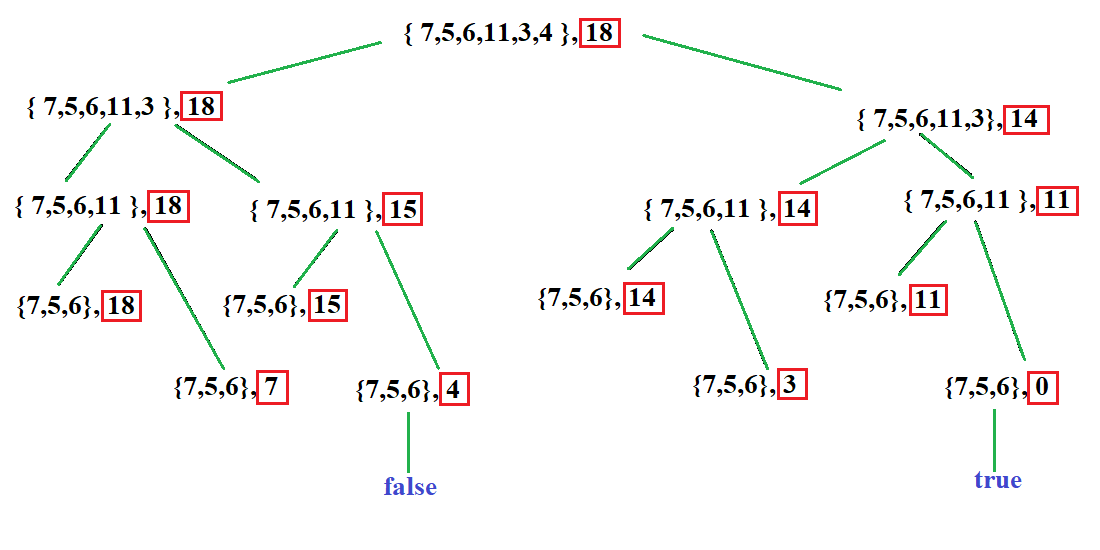
The space and time complexity of this method is:
The worst case time complexity for the above method will be O(2^n), where n is the total number of elements in the array.
The space complexity for the above method will be O(n), which will be used to store the recursion stack.
As we can see that the above solution has a high time complexity and is tedious to work on, we use a dynamic programming approach to reduce the number of repeated evaluations we are making at each step and instead store the result of a particular evaluation in order to use it again in future steps.
The quote below explains it best:

Dynamic Programming Approach
In this case, we create a two dimensional array of boolean elements which represent true or false depending on whether a subset can be created having sum equal to the row and with elements of this subset represented in the column. We decide whether to add an element into the subset or not depending on if its value is less than the sum or not. We fill the array in a bottom up manner till we reach the last element of the array, which will be the final answer.
The algorithm for this method is:
- For every elemnt i in the array and sum value s (incremented till it reaches value S/2),
- Check if the subset with sum equal to s can be formed by excluding the element i.
- Test the condition that the value of the element is less than s,
- If the above condition is true, check if the subset with sum equal to s can be formed by including the element i.
- If any of the above conditions are true, then store true into the value of the array at ith row and sth column, i.e. we can form the subset of elements with sum equal to s.
The code for this method is:
#include <bits/stdc++.h>
using namespace std;
bool partition (int arr[], int n)
{
int sum = 0;
int i, j;
for (i = 0; i < n; i++)
sum += arr[i];
if (sum % 2 != 0)
return false;
bool part[n + 1][sum / 2 + 1];
// initialize top row as false
for (i = 0; i <= sum/2; i++)
part[0][i] = false;
// initialize leftmost column as true
for (i = 0; i <= n; i++)
part[i][0] = true;
// Fill the partition table in botton up manner
for (i = 1; i <= n; i++)
{
for (j = 1; j <= sum/2; j++)
{
part[i][j] = part[i-1][j];
if (j >= arr[i - 1])
part[i][j] = part[i][j] ||
part[i - 1][j - arr[i -1]];
}
}
return part[n][sum/2];
}
int main()
{
int arr[] = {3, 4, 5, 6, 7, 11};
int n = sizeof(arr) / sizeof(arr[0]);
if (partition(arr, n) == true)
cout << "Can be divided into two subsets of equal sum";
else
cout << "Can not be divided into"
<< " two subsets of equal sum";
return 0;
}
For the given example the two dimensioal boolean table for the above solution will look like this:
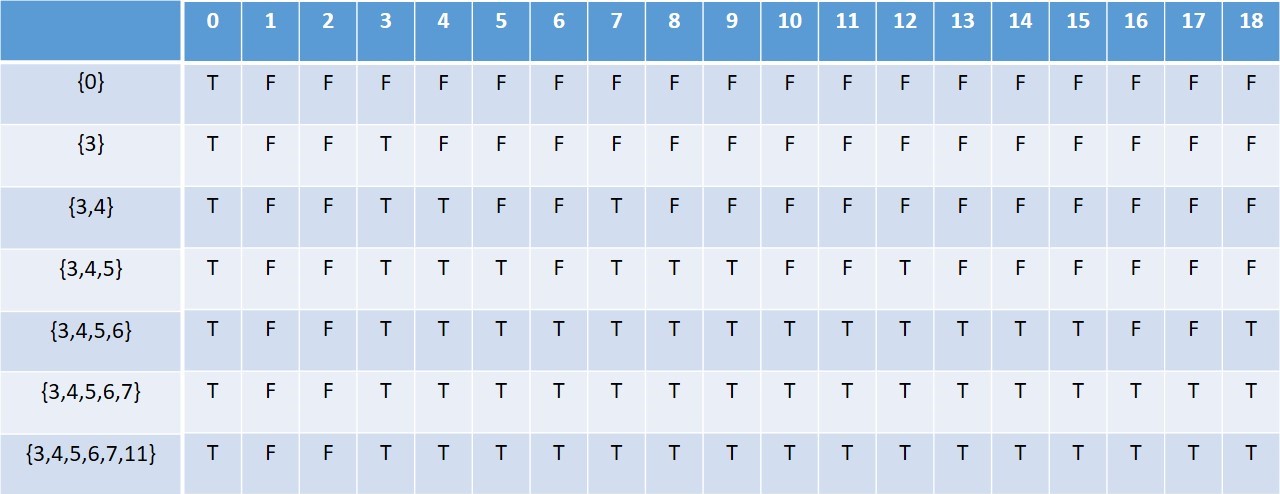
The space and time complexity of this method is:
The worst case time complexity for the above method will be O(n*s), where n is the total number of elements in the array and s is the value of the sum of all elements in the array.
The space complexity for the above method will be O(n*s), which will be used to store the dynamic two dimensional table of all the subsets along with their sum values.
Further work and applications
- The Partition problem is referred to as an NP-complete problem in computer science, and the above solution is a pseudo polynomial time dynamic programming solution. It is also referred to as "the easiest hard problem".
- Another optimisation version of the above problem is to partition a set into two subsets such that the difference in sums of the two subsets is minimum. This version of the problem is classified as NP-hard.
- The dynamic programming solution to this problem is similar to that of the knapsack problem, where a similar two dimensional table is maintained to check if the element in the row should be included or not in order to make the total sum equal to the value of the column.
Question 1
How does dynamic programming simplify the solution?
Question 2
The partition problem is an:
Question 3
If the elements in an array are {4, 6, 3, 5, 2, 9}, then what will the partitioned subsets be, such that their sums are equal?
With this article at OpenGenus, you must have the complete idea of solving this problem of partitioning a set into two subsets such that the sum of the two subsets are equal.
