Swap Nodes in Pairs

In this article, we have explained an efficient approach to Swap adjacent nodes in a Singly Linked List inplace. We have presented both Iterative and Recursive implementation.

Table of contents:

1. Problem Statement
2. Approach
3. Illustration
4. Iterative Solution
5. Recursive Solution

This is similar to Leetcode Problem 24. Swap Nodes in Pairs.

Problem Statement

We’re given the pointer to the head of a singly linked list, we're asked to reverse each two adjacent nodes and return the pointer/reference to the head of the list after swaping.

Before we begin we should know that we need to swap pointers/references not the values of each node so the value of each node remain the same.

Consider the following linked list:

We need to return a pointer to the head of this:

Note: if we had 6 at the end the new list will be 2=>1=>3=>4=>6=>5

Each node has a value and a pointer to the next node.

Approach

Before we solve, at the first thought you might say that, just swap pointers so that make 2 points to one and 4 points to 3 . Is it your first thought?
Let me tell you a problem here, if we change the 2 pointer to 1 we forgot that 1 also refering to 2 , so we're having some kind of circular referencing/pointers.

Then that doesn't work 😕.

Our approach to solve this problem is to fix this circular referencing in addition to some extra work.

1. We divide the list LOGICALLY into threes inclusive.
2. Then we're having at each group 1st node, 2nd node and 3rd node.
3. Change pointer of the 2nd node to point to the first node.
4. Change pointer of the 1st node to point to the 3rd node.
5. Keep track of the previous node by pointing to the second and then assigning to the first.
6. Repeat these steps for each group of threes(three nodes) until:
   1. We don't have remaining nodes (case even number of nodes)
   2. The next node of the first node is Null as only one node left (case odd number of nodes)

Illustration

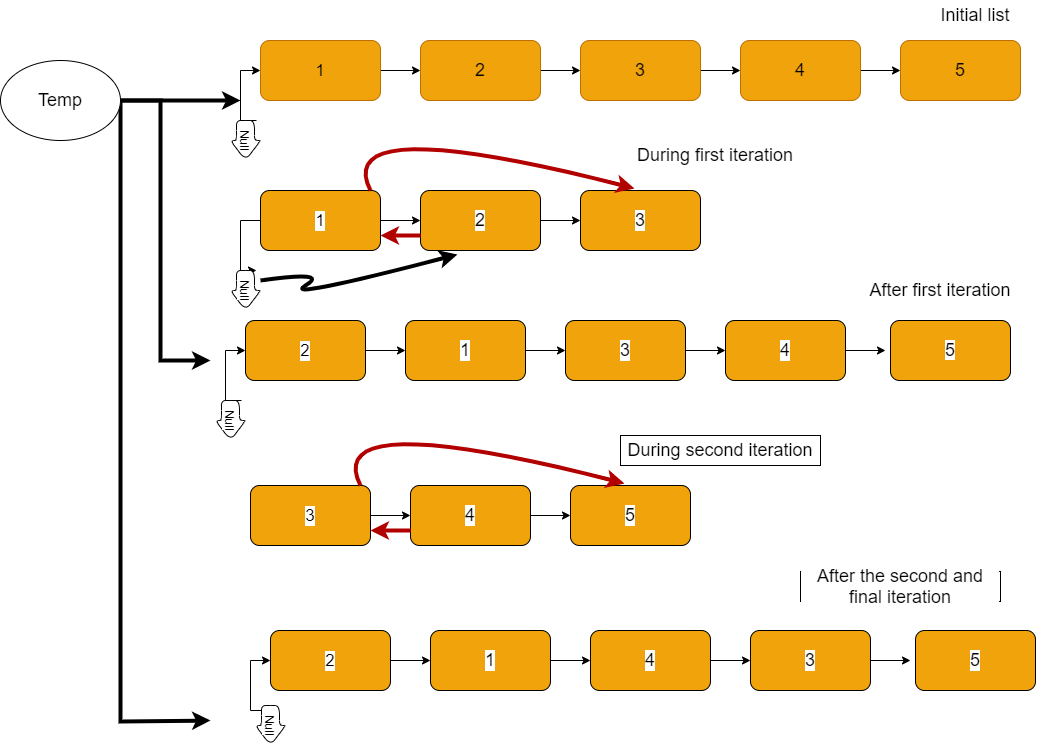
Temp is a pointer to the initial position of the head(temp.next=head_init_pos), whether the head changes its position, it still pointing to that initial position. That's for returning the whole list, if we returned the head then we will returning a list without the first element which will be the 2 in this case as the head is always 1.

Iterative Solution

Following is the implementation of the Iterative solution in Python:

# Singly-linked list Node structure
class ListNode(object):
    def __init__(self, val=0, next=None):
        self.val = val
        self.next = next
            
def swap_pairs(head):
    dummy = ListNode(0,head)
    prev, first = dummy, head
    while first and first.next:
        # There must be two nodes to swap
        # Specify the 2nd and 3rd
        second = first.next
        third = first.next.next
        # Our swap (the red arrows in the illustration)
        second.next = first
        first.next = third

        prev.next = second
        prev = first
        # Going to the next part
        first = third

    # If we print head then it will print the list
    # from position of the head which was 1 so it 
    # will print from thee second element position.
    return dummy.next

Runtime complexity

The runtime complexity of this solution is linear O(n), practically it won't iterate the whole list.

Space complexity

No additional memory required O(1) .

Recursive Solution

We can solve the problem recursivly.
Each time we treat 3rd as 1st and its next element as second and so on, and from bottom up we will have the following:
(1st->3rd) ---- (2nd->1st)
(5->None) ---- (None)
(3->5) ---- (4->3)
(1->3) ---- (2->1)

Following is the implementation of Recursive approach in Python:

def swap_pairs(head):
    first = head
    if (first == None or first.next == None):
        return first;

    second = first.next;
    third = second.next
    first.next = self.swapPairs(third);
    second.next = first;
    return second;

Time Complexity of Recursive approach

The Time Complexity is O(N). It is same as Iterative approach.

Space complexity of Recursive approach

We need n space for the recursion stack. Therefore, Space Complexity of recursive approach is O(N). Note that the space complexity of Iterative approach is O(1).

With this article at OpenGenus, you must have the complete idea of how to Swap Nodes in Pairs in a Singly Linked List efficiently.