
Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
In this post, we will design a Data Structure that returns the string occurring maximum and minimum times in constant time O(1). This will use a hashmap and a doubly linked list utilizing the advantages of each to solve the problem.
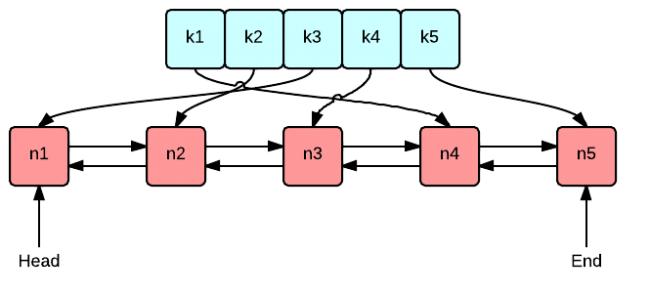
Table of contents:
- Problem Statement
- Naive Approach (Using a 2D doubly linked list)
- Optimized approach (Using hash map and doubly-linked list)
- Time & Space Complexity Analysis
To attempt similar problems on Designing Data Structure, go to this list.
This is similar to Leetcode Problem 432. All O'one Data Structure.
Problem Statement
The problem statement asks to design a data structure to store strings and their counts. It should be able to perform the following operations in constant time.
Increment key count, inc(key) -> Inserts a new key with count 1 or increments an existing key's count.
Decrement key count, dec(key) -> If key count is 1, we remove it, otherwise we decrement its count. If the key doesnt exist the function does nothing. It is guaranteed that the key exists in the data structure before this operation.
Get max key getMax(key) -> Returns one of the keys with the maximal count otherwise returns an empty string if no key exists.
Get min key, getMin(key) -> Returns one of the keys with the minimal count otherwise returns an empty string denoting no key exists.
Naive Approach (Using a 2D doubly linked list)
The idea is to use an ordered 2D doubly-linked list whereby each row corresponds to a count value and all keys in the same row have the same count value. I have used row and node interchangeably for simplicity in understanding.
Suppose we perform the following operations on this data structure;
- Increment "a" and "b" 4 times.
- Increment "c" and "d" 3 times
- Increment "e" 2 times
- Increments "f" and "g" 1 time
Here is what our result would look like after additional operations after the ones above.
Once a key is incremented, move the key from current row to last row if the last row count = current_row.count + 1, otherwise insert a new row before the current row with its count as current_row.count + 1.
When a key is decremented, move the key from current row to last row if last_row.count = current_row.count - 1, otherwise insert row after current row, its count is current_row_count - 1.
With this approach getting the maximal value and minimal value is in constant time O(1), we just return the first key in the first row for the maximal count and first key in last row for the minimal count in constant time O(1) provided the rows are in descending order.
The problem with this approach is we have to do more work to maintain this descending order when we either increment key or decrement key, which makes the time complexity linear O(n).
This could be improved by incorporating a data structure known for its efficient access time done in constant time. A hash map. You can learn more about how it does this in link at the end of this post.
In the mean time we shall discuss this approach below.
Optimized approach (Using hash map and doubly-linked list)
In this approach, the idea is to use a doubly linked list which will result in O(1) operations for insertions and deletions, head will have the largest count and tail least count. Therefore the head will return the maxKey and tail the minKey in constant time. We use the hashmap for referencing the list nodes for efficient access times which was our problem in the previous naive approach.
Increment.
Condition 1: Key exists in the list
- Check if key is at the first row.
- If the above condition stands, create and insert a new row before the current with its count value as currentRow.count + 1 and its data as the key(string).
- Otherwise remove the key(string) from current row and place it in the row before the current row whos count is currentRow.count + 1.
Condition 2: Key does not exist in the list.
- Check if the list is empty.
- If the above condition stands, create and insert a new node with a count of 1 to the end of the list with key(string) as its data.
- Otherwise a node exists so place the key(string) in the existing node at the end of the list.
Decrement.
Condition 1: Key exists in the list
- Check if node with key has a value of 1, if so remove it from the list.
- Check if key is at the first node.
- If the above condition stands, create and insert a new row after the current with its count value as currentRow.count - 1 and its value as the key(string).
- Otherwise remove the key(string) from current node and place it in the last row of the list.
Condition 2: Key does not exist in the list.
The key does not exist in the list so do nothing.
getMax().
- Check wheather the list is empty and return nothing.
- Otherwise return the first node's first key.
getMin().
- Check wheather the list is empty and return nothing.
- Otherwise return last node's first key.
Code.
class AllOne{
public:
//create the structure of a row
struct row{
list<string> strings;
int val;
row(const string &s, int x) : strings({s}), val(x){}
};
//initialize hashmap and doubly linked list
unordered_map<string, pair<list<row>::iterator, list<string>::iterator>> strMap;
list<row> strList;
//increment procedure
void inc(string key){
//the key does not exist in the map
if(strMap.find(key) == strMap.end()){
if(strList.empty() || strList.back().val != 1){
auto newRow = strList.emplace(strList.end(), key, 1);
strMap[key] = make_pair(newRow, newRow->strings.begin());
}else{
auto newRow = --strList.end();
newRow->strings.push_front(key);
strMap[key] = make_pair(newRow, newRow->strings.begin());
}
}else{
//key exist in the map
auto row = strMap[key].first;
auto col = strMap[key].second;
auto lastRow = row;
--lastRow;
if(lastRow == strList.end() || lastRow->val != row->val + 1){
auto newRow = strList.emplace(row, key, row->val + 1);
strMap[key] = make_pair(newRow, newRow->strings.begin());
}else{
auto newRow = lastRow;
newRow->strings.push_front(key);
strMap[key] = make_pair(newRow, newRow->strings.begin());
}
row->strings.erase(col);
if(row->strings.empty())
strList.erase(row);
}
}
void dec(string key){
//key does not exist in the map
if(strMap.find(key) == strMap.end())
return;
else{
//key exists in the map
auto row = strMap[key].first;
auto col = strMap[key].second;
if(row->val == 1){
row->strings.erase(col);
if(row->strings.empty())
strList.erase(row);
strMap.erase(key);
return;
}
auto nextRow = row;
++nextRow;
if(nextRow == strList.end() || nextRow->val != row->val - 1){
auto newRow = strList.emplace(nextRow, key, row->val - 1);
strMap[key] = make_pair(newRow, newRow->strings.begin());
}else{
auto newRow = nextRow;
newRow->strings.push_front(key);
strMap[key] = make_pair(newRow, newRow->strings.begin());
}
row->strings.erase(col);
if(row->strings.empty())
strList.erase(row);
}
}
//get first key in first row in the map
string getMax(){
if(strList.empty())
return "";
return strList.front().strings.front();
}
//get the first key in the last row in the map
string getMin(){
if(strList.empty())
return "";
return strList.back().strings.front();
}
};
Time & Space Complexity Analysis
By using the hashmap we track the position of a key, access time is O(1) and using a linked list for storing nodes, increments and decrements will also be O(1). Overally the operations run in constant time O(1)
The space complexity on the other hand will be linear O(n), n being the number of keys we need to store.
Questions
Can you think of a real world application for this data strcuture?

