The problem we will try to solve is to find the Number of ways to reach a given number (or a score in a game) using increments of 1 and 2 with consecutive 1s and consecutive 2s allowed.

The problem statement may seem complex when you read at first, but, it's actually very simple. Given a number, find the number of ways to reach it using 1 and 2. For a number, let's say X, we need to find the number of ways in which by adding 1 and 2 we can reach upto X. This can be also seen as a game where a player has to get the X points. For this problem consecutive 1s and 2s are allowed.

Given an example:

10
1+1+1+1+1+1+1+1+1+1
2+2+2+2+2
2+2+2+2+1+1
2+2+2+1+1+1+1
2+2+1+1+1+1+1+1
2+1+1+1+1+1+1+1+1

4
1+1+1+1
2+2
1+2+1

From the example above, it is clear that the number of ways to reach 10 is 6 and for 4 is 3.

This problem can be expanded to include increments of not only 1 and 2, but other numbers as well.

We will take two approaches:

• Brute force approach O(2^N) time
• Dynamic Programming approach O(N) time

Brute Force Approach

Let's take an array to store 1 and 2 and call it A[].

int A[] = {1,2}

The logic is actually a simple one, we run a recursive algorithm considering two conditions

i) Solutions that do not contain A[i]
ii) Solutions that contain atleast one A[i]

The core logic can be written in one line

 return count(A,n-1,X) + count(A,n,X-A[n-1])

X here is the number that we are ultimately trying to form with the available array, and n being the size of the array A which, in this case is 2. And count() is the recursive method that returns the number of ways we can reach X.

count(A,n-1,X) implies that the solution isn't considering one of the values of A

count(A,n,X-A[n-1]) This here implies the condition ii we include at the least case one A[i], hence the repeated subtraction of the A[i] till we arrive at 0.

Implementation of the above logic

#include<iostream>
using namespace std;

int count(int A[], int n, int X){
if(X==0) 
  return 1;
if(X<0)
  return 0;

if(n<=0 && X>=1)
 return 0;
 
 return count(A,n-1,X) + count(A,n,X-A[n-1]);
}

int main(){
int A[]={1,2};
cout<<count(A,2,4);
return 0;

Output

3

What the algorithm does?

It's a recursive function, therefore, a base condition is compulsory.

In case X=0 which is an ideal case as it implies that after few subtractions we now have reached X we return 1 as it is a part of the solution.
X<0 the path we choose to reach X hasn't fetched X, hence we return 0.
n<=0 && X>=1 in the condition i) we said that we won't be considering a number, and for that case in the recursive call we have called for n-1. Now in this case there is a good chance that n has become zero and X is still positive which shows that our path hasn't fetched X.

The remaining part of the code is a simple main function.

Now a lot of you might have already felt that the algorithm was unnecessary and since we are using only two numbers to form X, which is 1 and 2, then why take array and that calculation?
Well, you're right, perhaps the algorithm was given to explain its substructure and why we will be employing dynamic programming.

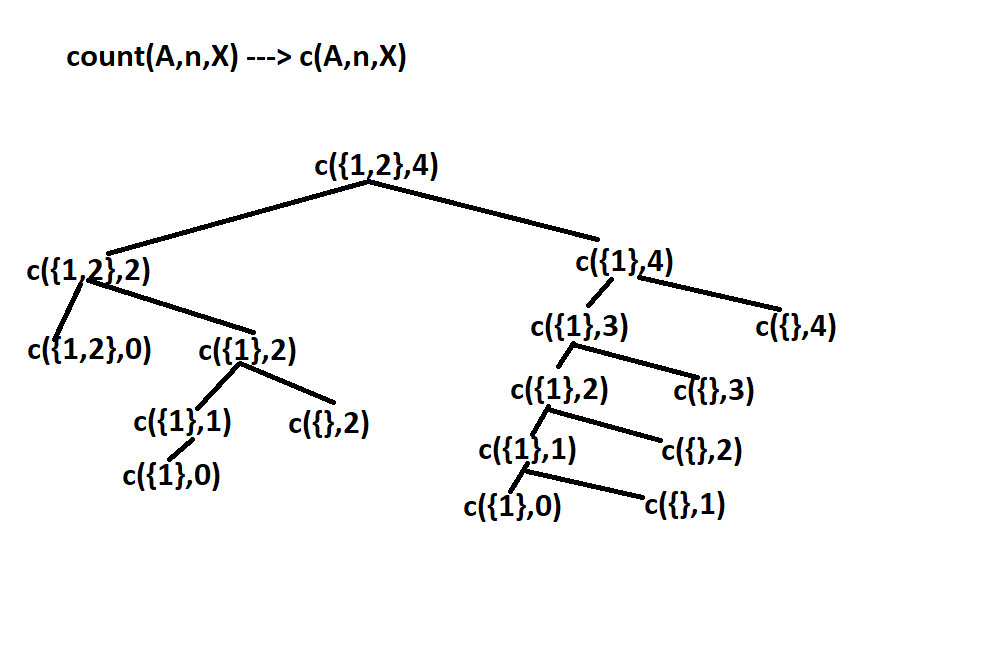
As seen in the diagram above same subproblems are being called again and again increasing the time complexity.

Since there are overlapping subproblems we use a table to store the intermediate results. Following the brute force, we shall solve the problem using dynamic programming.

Dynamic Programing

In contrast to the previous approach, we eliminate the entire array A[], instead we take the array table[] to store the results of the subproblems to avoid recalculating. Also unlike the top down approach of the brute force algorithm, we are using a bottom up approach to build the table.

table[X] = number of ways to reach sum X using 1 and 2

The idea is very simple, we take a table of size X+1 and fill it with the increments of 1 and 2. And return table[X] which gives us the answer. The relation is simple as well:

table[X] = table[X-1] + table[X-2]

The base case are as follows:

table[1] = 1
table[2] = 2 // 2 = 2 or 1 + 1

Prior this increment, we initialize the table with 0 just to avoid any anonymous or junk values.
We can also use the c++ predefined function memeset for this purpose

memeset(table,0,sizeof(table))

We initialize table[0]=1, as there is only one way to reach that score 0.

Now for the core logic, as mentioned above we create a table and store all the scores starting from 0 to X

 for i in 1 to X
   table[i]+= table[i-1]
 for i in 2 to X
   table[i]+=table[i-2]

Since we are only considering increments of 1 and 2, we wrote for 1 and 2, we have to repeat the same loop for any additional increments.
table[i-1] implies that if we increment by 1, we still have X-1 steps left.
After the first loop we'd get
1 1 1 1 1

That's basically the only solution (1+1+1+1) for X=4.
table[i-2] takes two steps at a time or increments by 2. The point to note here is that the second loop is dependent on the first one as it is the same table. If you take two different tables then it would mean a separate thing.

Example

for X=4 using 1
we'd get 1+1+1+1
for X=4 using only 2
we'd get 2+2
but to get the optimal result we need to combine both 1 and 2. Hence we use the same table for the calculations.
After the second loop we'd get
1 1 2 2 3
At the end of the function we simply return table[X] which is 3 in this case.

Implementation of the above explanation

#include<iostream>
using namespace std;

int count(int X){
int table[X+1],i;
for(i=0; i<=X; i++)
   table[i]=0;
   
table[0]=1;
 for (i = 1; i <= X; i++) 
    table[i] += table[i - 1];
  for (i = 2; i <= X; i++) 
    table[i] += table[i - 2]; 

return table[X];
}

int main(){
    cout<<count(10);
}

Output

6

Time Complexity

Unlike the previous time complexity, we have achieved a better linear O(n) time complexity.

Talking about space, the space for the previous algorithm was O(n) where n was the size of the array, which is 2, which is significantly negligible to the current algorithm's time complexity which is O(X) where X is our target score/number.

Applications

1. This problem in many ways is similar to the famous "Coin Change problem", one of the important problems to understand dynamic programming.
2. Dynamic Programming in general has found to be very useful in optimization problems.

Further Reading