In this article we will see how AdaBoost works and we will see main advantages and disadvantages that lead to an effective usage of the AdaBoost algorithm.

How Adaboost works

The basis of this algorithm is the Boosting main core: give more weight to the misclassified observations.

In particular, AdaBoost stands for Adaptive Boosting, meaning that the meta-learner adapts based upon the results of the weak classifiers, giving more weight to the misclassified observations of the last weak learner (usually a decision stump : one level decision trees, meaning that the tree is made based upon one decision variable and it's composed by a root and all the childs directly connected to the root)

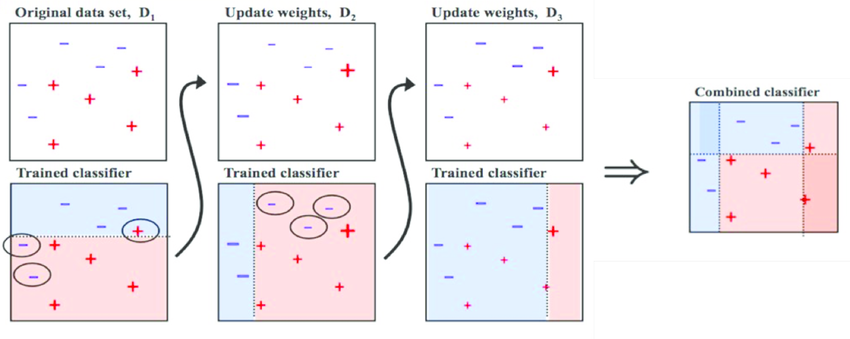
Notice the circled + and - signs: They are growing if misclassified, otherwise they reduce if correctly classified.
And here we can see the meta-learner (weighted sum) general form:

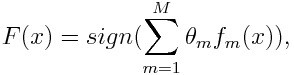
Where f corresponds to the weak learner and theta stands for the weight associated to the specific weak classifier.

The specific algorithm implementation of vanilla AdaBoost consist of the following phases, given the assumptions:

Assumptions : Given a training set made of m observations in the form of tuples (x,y), where x belongs to X (the set of possible values of the dependent variables) and y belongs to the set {-1,1} meaning that we are considering a classification problem (vanila AdaBoost is only possible in classification problems).

1. We initialize the weight distribution that will model the weak learner choiches as the inverse of the number of observations (1/m , equiprobability among observations, meaning that is a normalized distribution: the sum of the distributions for the m observations is 1).

2. Iteratively, for T iterations:

2.1. We train the weak classifier using the probability distribution defined above.
2.2. The weak classifier is used to predict the set of data, the predictions are used to calculate an error metric that is a sum of the weak learner values of the prediction that are misclassified (meaning that they are mismatching in confront of the real value y).
2.3. We calculate the weight associated to the specific weak learner based on the error: we give more weight if the error is high.
2.4 We then update the initial distribution of the weak classifier for the next iteration, based upon the weight associated to the weak learner: We give a higher weight to observations not correctly classified and lower to the correctly classified ones. The distribution mantain the property of normality thanks to a normalization factor.

3. Then We finally output the final value associated to wichever hypotesis we want (especially a not tested one, testing set) given hypotesys based on the sign function (a function that gives as an output the values -1 or 1 based on the sign of the argument of the function) of the sum of the T products between the weak learners predictions and the associated weights to the specific weak learner.

The implementation above suggests that the algorithm works iteratively on every observation of the data, in which observation after observation the algorithm adjust the weight on data according to the correctness or not of the prediction (step 4).

Moreover the order of magnitude of the weight is given by the error magnitude (step 3). In particular, we see that we can see this as testing an hypothesis on our data at every iteration(step 1) and the output is given by an approximation (or better called in this case activation) that gives us a final hypothesis (last step).

As we can see the algorithm is constructed in order to give more weight to the misclassified observations and less to the correct classified one (see step 4 of the pseudocode). And in step 3 we can see that the classification error, epsilon, influences directly the weight given to the specific observation in the next algorithm iteration.

Advantages and Disadvantages

AdaBoost, with decision trees as weak learners, is often referred to as the best out-of-the-box classifier. In some problems it can be less susceptible to overfitting than other algorithms (see below for more informations).

The individual learners can be weak, but as long as the performance of each weak learner is better than random guessing, the final model can converge to a strong learner (a learner not influenced by outliers and with a great generalization power, in order to have strong performances on uknown data).

Meanwhile it has a lot of advantages, AdaBoost have one main disadvantage:

AdaBoost is sensitive to noisy data and outliers.

Meaning that whenever the data are not easily amenable to a specific separation plane (with acceptable performances based upon the model objective. For example the weak learners have to be better than random guessing), it's harder that the meta-learner converges to a strong learner without overfitting (Given the AdaBoost characteristic to give more weight to the misclassified observations: if there are a lot of outliers the trained weak learners would be very different between them and very specific to the zone of the misclassified observations, creating a very specific model, increasing overfitting on the training data).

So we can say that AdaBoost works best when we clean up the dataset from outliers .

Basic implementation (in Python)

Here we can see a little implementation of the AdaBoost algorithm in Python (with scikit-learn):

Load libraries

from sklearn.ensemble import AdaBoostClassifier
from sklearn import datasets
# Import train_test_split function
from sklearn.model_selection import train_test_split
#Import scikit-learn metrics module for accuracy calculation
from sklearn import metrics

Load and split (in train and test) data

iris = datasets.load_iris()
X = iris.data
y = iris.target

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3)

Create adaboost classifer object

abc = AdaBoostClassifier(n_estimators=50,
                         learning_rate=1)

Train Adaboost Classifer

model = abc.fit(X_train, y_train)

Predict the response for test dataset and evaluate accuracy

y_pred = model.predict(X_test)

print("Accuracy:",metrics.accuracy_score(y_test, y_pred))

You can test it yourself, just copy and paste it in your favourite IDE, play with it, then execute!

Conclusion

Now you can jump right into implementing effectively AdaBoost with wichever languaguage and library you want: Python with scikit-learn (as seen above), R with caret, Julia and many more.

Learn more:

• Understand different types of Boosting Algorithms by Naseem Sadki (OpenGenus)
• Gradient Boosting by Harsh Bansal (OpenGenus)
• XGBoost by Prashant Anand (OpenGenus)