Young Tableaus data structure

Young Tableaus data structure is a unique form of matrix in which all elements of a row are in sorted order from the left to right and that of a column are in sorted order from top to bottom.

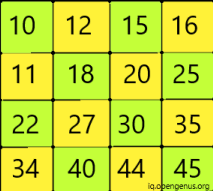
We can perform different operations on this matrix. In this article we will discuss the below mentioned functions:

• Insertion of element
• Search for an element
• Deletion of element
• Replace an element

Some values are infinity to signify invalid value.

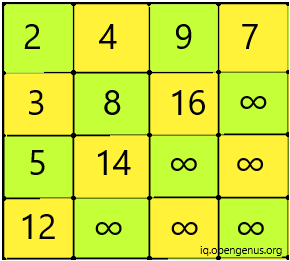
In this problem, we start from the bottom right element and then move it in upward direction or leftward direction as and when required.

Insertion

There are two things that we need to take care of while inserting new values.

• To find the initial starting position
• To find the correct position

Firstly, we start from the corner position and iterate to find the correct position.

void position(int matrix[][N], int i, int j)
{
    if (i == 0 && j == 0) {
        return;
    }
    if (i == 0)
    {
        if (matrix[i][j] < matrix[i][j-1]) {
            swap(matrix[i][j], matrix[i][j-1]);
            position(matrix, i, j - 1);
        }
        return;
    }
    if (j == 0)
    {
        if (matrix[i][j] <matrix[i-1][j]) {
            swap(matrix[i][j], matrix[i-1][j]);
            position(matrix, i - 1, j);
        }
        return;
    }
 
    if (matrix[i][j] < matrix[i-1][j]) 
    {
        swap(matrix[i][j],matrix[i-1][j]);
        position(matrix, i - 1, j);
    }
 
    if (matrix[i][j] < matrix[i][j-1]) 
    {
        swap(matrix[i][j], matrix[i][j-1]);
       position(matrix, i, j - 1);
    }
}
std::fill(*matrix, *matrix + M*N, INT_MAX);
void initial(int matrix[][N], vector<int> &keys)
{
    for (int key: keys)
    {
        if (matrix[M-1][N-1] != INT_MAX) {
            cout<<"Cannot Insert key!"<<endl;
        }
        else {
            matrix[M-1][N-1] = key;
            position(matrix, M-1, N-1);
        }
    }
}
 

• Firstly, we will insert infinity at all cells.
• Then, we check if the tableau is already full then we won't be able to insert the new key. As a result, we check if value at index [m-1][n-1] is infinity or not.
• If so then we cannot insert new value else we will insert a new value at last index [m-1][n-1].
  Function Position is called:
• Then we start to check the correct position for the value within the tableau.
• The base case is if the i and j values are 0. This mean we are at the first cell of our matrix.
• Then we recursively check for rows and columns for the correct position. We check if the correct next value is smaller than current then we swap them. This fashion follows recursively.

The Time Complexity is O(n+m).

Searching Operation:

For searching a specific element we can opt for naive approach. But that would have O(m * n) time complexity. However, since our matrix has a specific feature that all elements in row and column are sorted, we can use that feature.

We can start searching operation from the top right most corner and then do comparisons to find our desired element.

bool find(int matrix[][N], int key)
{
    int i = 0, j = N - 1;
    while (i < M && j >= 0)
    {
        if (matrix[i][j] < key) {
            i++;
        }
        else if (matrix[i][j] > key) {
            j--;
        }
        else {
            return true;
        }
    }
    return false;
}

In above function find(), we start searching and

• If the current element is less than our required element then we increment our row index
• If current element is more than desired element then we decrement the column index
• If our current element matches the desired element then we return true else false.

The Time Complexity is O(m+n)

Delete Operation

To delete an operation we will find the element, make it equivalent to infinity and then place it at its correct new location.

void fixmatrix(int matrix[][N], int i, int j)
{
    int bottom = (i + 1 < M) ? matrix[i + 1][j] : INT_MAX;
    int right = (j + 1 < N) ? matrix[i][j + 1] : INT_MAX;
 
    if (bottom < right) 
    {
        swap(matrix[i][j], matrix[i + 1][j]);
        fixmatrix(matrix, i + 1, j);
    }
 
    if (bottom > right)
    {
        swap(matrix[i][j], matrix[i][j + 1]);
        fixmatrix(matrix, i, j + 1);
    }
}
void delete(int matrix[][N], int i, int j)
{
    matrix[i][j] = INT_MAX;
    fixmatrix(matrix, i, j);
}

Here, we call delete function that initialise the value with infinity. Then we call fixmatrix function to fix the correct location for this cell.

• Firstly, we try to get the values at the bottom and right cell of the current cell using ternary operator.
• Then, we recursively traverse downwards.
• Then, we recursively traverse upwards.

The Time Complexity is O(n+m)

Replace Operation

What if we want to replace an element in the matrix?
To do so:

• Find the location of the element to be replaced.
• Replace the element with infinity and fix its correct new position
• Place the new element (replacement) at bottom right corner and then fix its new correct position.

We can use the above defined functions to accomplish this operation.

void fixmatrix(int matrix[][N], int i, int j)
{
    int bottom = (i + 1 < M) ? matrix[i + 1][j] : INT_MAX;
    int right = (j + 1 < N) ? matrix[i][j + 1] : INT_MAX;
 
    if (bottom < right) 
    {
        swap(matrix[i][j], matrix[i + 1][j]);
        fixmatrix(matrix, i + 1, j);
    }
 
    if (bottom > right)
    {
        swap(matrix[i][j], matrix[i][j + 1]);
        fixmatrix(matrix, i, j + 1);
    }
}

void position(int matrix[][N], int i, int j)
{
    if (i == 0 && j == 0) {
        return;
    }
    if (i == 0)
    {
        if (matrix[i][j] < matrix[i][j-1]) {
            swap(matrix[i][j], matrix[i][j-1]);
            position(matrix, i, j - 1);
        }
        return;
    }
    if (j == 0)
    {
        if (matrix[i][j] <matrix[i-1][j]) {
            swap(matrix[i][j], matrix[i-1][j]);
            position(matrix, i - 1, j);
        }
        return;
    }
 
    if (matrix[i][j] < matrix[i-1][j]) 
    {
        swap(matrix[i][j],matrix[i-1][j]);
        position(matrix, i - 1, j);
    }
 
    if (matrix[i][j] < matrix[i][j-1]) 
    {
        swap(matrix[i][j], matrix[i][j-1]);
       position(matrix, i, j - 1);
    }
}

void replace(int matrix[][N], int i, int j, int key)
{
    matrix[i][j] = INT_MAX;
    fixmatrix(matrix, i, j);
    matrix[M-1][N-1] = key;
    position(matrix, M-1, N-1);
}

bool find(int matrix[][N], int key)
{
    int i = 0, j = N - 1;
    while (i < M && j >= 0)
    {
        if (matrix[i][j] < key) {
            i++;
        }
        else if (matrix[i][j] > key) {
            j--;
        }
        else {
            replace(matrix,i,j,val);
            return true;
        }
    }
    return false;
}

• In this operation, we used the fixmatrix and position function as defined before. - However, we created a replace function that called the fixmatrix and position function.
• The replace function is called inside find function. Inside the find function, if we find the exact match for our value then we call replace function to replace the cell with new value.
• Then, use fixmatrix and position functions to find and fix the correct new location.

The Time Complexity is O(n+m)

Hence, through this article we will get a good idea about the basic operations that can be performed on Young Tableaus Data Structure.
Happy Coding!