
Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
In this article we will discuss the approach to find out the nodes at k distance from the given node.
Let us assume we have a binary tree. Let the node given to us be 'Target Node'. Now, we need to find all nodes at distance k from 'Target Node'. Those k nodes could be parent as well as child nodes of the 'Target Node'.
Below is the code that represents the implementation of the Tree:
class Tree{
int value;
Tree right;
Tree left;
}
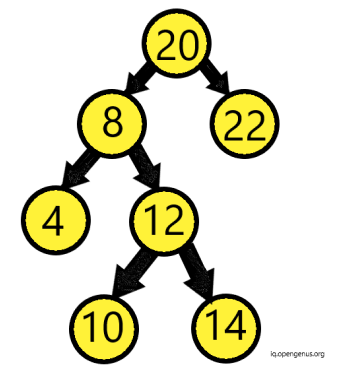
We can follow two major techniques:
1. Breadth First Traversal:
In this method, we perform the Breadth First Search and recursively print the k left child nodes of 'Target Node'. Then in similar fashion print the k right nodes of 'Target Node'. Afterwards, we can traverse the parent node.
2. Percolate Distance:
In this method, we perform the Depth First Search and then at each node, we calcuate the distance from the 'Target Node'.
Breadth First Traversal:
1.For the first approach of Breadth First Search we have to convert the binary tree to a Undirected graph.
We can follow either of below approaches :
- The graph can be made by post-order traversal.
- We can make adjacency list or adjacent matrix.
2.Now, using Breadth First Search, we will find the k nodes around our 'Target Node'. We will keep storing them in array.
3.We return the array containing all nodes.
Complexity Analysis:
- The space complexity will be O(n), Since we go to each node twice when we make graph
- The time complexity will be O(n), Assuming the graph to be sparse the space is equivalent to the total number of nodes
Implementation:
//We use Graph Function to make a graph
void Graph(Tree* root, unordered_map<int, vector<int>> &graph){
if(root == nullptr){
return;
}
int val = root->val;
if(root->left){
int left = root->left->val;
graph[val].emplace_back(left);
graph[left].emplace_back(val);
}
if(root->right){
int right = root->right->val;
graph[val].emplace_back(right);
graph[right].emplace_back(val);
}
Graph(root->left, graph);
Graph(root->right, graph);
}
public:
//function to calculate distance of nodes from target
vector<int> distanceK(Tree* root, Tree* target, int K) {
if(root == nullptr || target == nullptr || K < 0){
return {};
}
if(K == 0){
return {target->val};
}
// call function Graph to make graph
unordered_map<int, vector<int>> graph;
Graph(root, graph);
// BFS to find target node
unordered_set<int> visited;
queue<pair<int, int>> q;
q.emplace(make_pair(target->val, 0));
//vector to store nodes
vector<int> result;
while(!q.empty()){
pair<int, int> curr = q.front();
q.pop();
visited.insert(curr.first);
for(auto &neighbor : graph[curr.first]){
if(visited.count(neighbor) == 0){
int distance = curr.second + 1;
if(distance == K){
result.emplace_back(neighbor);
}
else if(distance < K){
q.emplace(make_pair(neighbor, distance));
}
}
}
}
return result;
}
Explanation:
- For above tree, firstly we check if the root or target is NULL or if the distance k is less than 0. If so, then we return.
- If k is equivalent to 0 then we return the value of the node since it means that we have reached the target node back.
- Then, we build a graph by traversing through its left and right subtree and inserting values recursively.
- For Breadth First Search, we first create unordered set named "visited" to keep a track of all visited nodes and a queue named "q". The queue will keep pairs of node along with its corresponding distance from target.
- Then we make vector "result". It will store the final result.
- Now, we enter a while loop that traverses until the queue "q" is empty. This means it will keep iterating until all neighboring nodes of target have been visited.
Within While Loop:
- We make a pair "curr", It represents the current pair of node and its distance. We store this value from the top value of queue "q" and then pop that value from "q".
- Then, this value is stored in visited vector to keep a record of visited nodes.
Then, we enter another for loop: - Then we check if the visited count is 0. If so, the we declare variable "distance" and initialize it with second value of "curr" (i.e. the distance) + 1.
- Now, if the distance becomes equivalent to "k" then we will insert this node to result vector. Else if the distance is less than k, then we must keep iterating. Hence, we insert pair of neighbor and its distance to queue "q".
- In the end after the queue is empty, we get out of our while loop and return result.It will contain all neighboring k nodes of our tree.
With below approach we can find out the nodes for our tree at k distance.
Percolate Distance:
In this method, we traverse the tree and check if the current node is the 'Target Node'. When we get them we perfrom the pre-order traversal to find all neighboring nodes at k distance.
In this method, the striking difference is that we consider the target node as the root node.
Consider an example, Suppose we have a root node from which our target node is at distance 3, in right branch. Then, any node at distance k-3 in left branch will be returned.
Complexity Analysis:
- The space complexity will be O(n)
- The time complexity will be O(n)
Implementation:
There are 4 key steps that we take care of :
- If the root==target then return all nodes in the subtree at distance k.
- If the target lies in left subtree of node at distance 'm', then we will find the nodes at distance k-m in right branch.
- In similar fashion we move forward with right branch of node.
- If we cannot find target in either branch of the tree then we will stop.
void percolate(tree *root,int k)
{
if(root==NULL || k<0)
return ;
if(k==0)
{
cout<<root->data<<" ";
return;
}
percolate(root->left,k-1);
percolate(root->right,k-1);
}
int print(tree *root,tree *target,int k)
{
if(root==NULL)
return -1;
if(root==target)
{
percolate(root,k);
return 1;
}
int left = print(root->left,target,k);
int right = print(root->right,target,k);
if(left!=-1)
{
if(left==k){
cout<<root->data<<" ";
}
percolate(root->right,k-left-1);
return left+1;
}
if(right!=-1)
{
if(right==k){
cout<<root->data<<" ";
}
percolate(root->left,k-right-1);
return right+1;
}
return -1;
}
Explanation:

We can follow the below approach to traverse our above tree taken as example and find the k nearest neighbors.
Percolate function is a recursive function that traverses left and right sub-tree of our given tree.
-
Firstly, let's understand the percolate function. If the root is null or k is smaller than 0, we return.
-
If k is 0 then we return the value of node and return.
-
In the print function, we have root of tree, target and distance k as arguments. If the root is null we return -1.
-
If the root is equivalent to the target we call percolate function with root and k as arguments.
-
Then, we declare "left" integer variable and store the value returned by function print in it recursively. This is to check if there is any null node. If there is a null node then value of -1 will be returned to "left".
-
Similar to "left", we have "right". We follow same procedure for the right subtree too.
-
Now, if the left is not equal to -1, that is it does not encounter null node, then we check the following:
If the left is equivalent to "k" then we print the value of left i.e root->data.
Since this means that the node is located at distance.
Then we call percolate function again, with distance "k-left-1", because we are going to node that is one step away from the current node. Hence,at left-1 distance. And since we have to traverse k nodes hence k-left-1. -
In similar fashion, we check value for "right" integer variable and traverse the nodes.
-
In the end we would have printed all the nodes at k distance in our tree.
Using these approaches we can find the nodes at distance k from the target node.
Happy Coding!
