Reading time: 35 minutes | Coding time: 15 minutes

Bloom Filter is a probabilistic Data Structure that is used to determine whether an element is present in a given list of elements. Bloom Filter is quite fast in element searching, however being probabilistic in nature it actually searches for an element being "possibly in set" or "not in set at all which makes a crucial difference here and this is what makes Bloom Filter efficient and rapid in its approach.

The Bloom Filter Data Structure is closely associated with the Hashing Operation which plays an important role in this probablistic data structure which we will further discuss. The advantages of this Data Structure is that it is Space Efficient and lightning fast while the disadvantages are that it is probablistic in nature.

Even though Bloom Filters are quite efficient, the primary downside is its probablistic nature. This can be understood with a simple example. Whenever a new element has to be searched in a List, there are chances that it might not be entirely in the list while similar chances are there that it might be in the set. If there is the possibility of the element in the set, then it could be a false positive or true positive. If the element is not entirely present in the set, then it can be remarked as true negative. Due to its probablistic nature, Bloom Filter can generate some false positive results also which means that the element is deemed to be present but it is actually not present. The point to be remarked here is that a Bloom Filter never marks a false negative result which means it never signifies that an element is not present while it is actually present.

Understanding the Concept of Hashing and Bloom Filter

To understand the concept of Bloom Fliter, we must first understand the concept of Hashing. Hashing is a computational process where a function is implemented which takes an input variable and it return a distinct identifier which can be used to store the variable. What makes Hashing so popular is that it is quite simple to implement and it is much more efficient compared to the conventional algorithms for performing various operations such as insertion and search.

In the Bloom Filter Data Structure, Hashing is an important concept. However a Bloom Fliter which holds a fixed number of elements can represent the set with a large number of elements. While the numbers are added to the Bloom Filter Data Structure, the false positive rate steadily increases which is significant since Bloom Filter is a probabilistic data structure.

Unlike other Data Structures, Deletion Operations is not possible in the Bloom Filter because if we delete one element we might end up deleting some other elements also, since hashing is used to clear the bits at the indexes where the elements are stored.

When a Bloom Filter is initialized, it is set as a Bit Array where all the elements are initialized to a default value. To insert an element, an integer value is needed which is hashed using a given Hash Function a given number of times. The bits are set into the Bit Vector and the indexes where the elements are added are intialized to 1.

The Search Operation in a Bloom Filter is also performed in the same manner.

Whenever a Search Query is passed, the index bit is checked to verify if the element is present or not. In case, any one of the index bit is not present, it is presumed that the element is not present in the Bloom Filter Vector. However, if all the bits are 1, then it is made sure that the element is definitely present. There is no such case where it is presumed that a false is returned if an element is actually present.

Insertion and Search Operation in Bloom Fliter

To insert an element into the Bloom Filter, every element goes through k hash functions. We will first start with an empty bit array with all the indexes intialized to zero and 'k' hash functions. The hash functions need to be independent and an optimal amount is calculated depending on the number of items that are to be hashed and the length of the table available with us.

The values to be inserted are hashed by all k hash functions and the bit in the hashed position is set to 1 in each case. Let us take some examples:

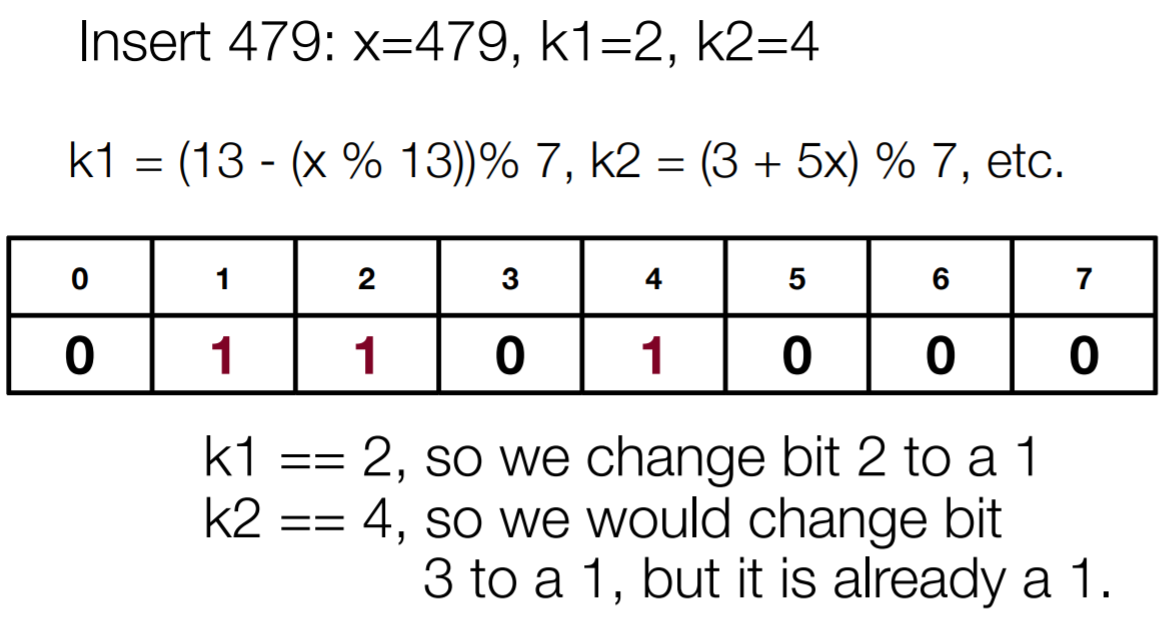
To check if an element is already present in the Bloom Filter, we must again hash the search query and check if the bits are present or not. Let us take an example:

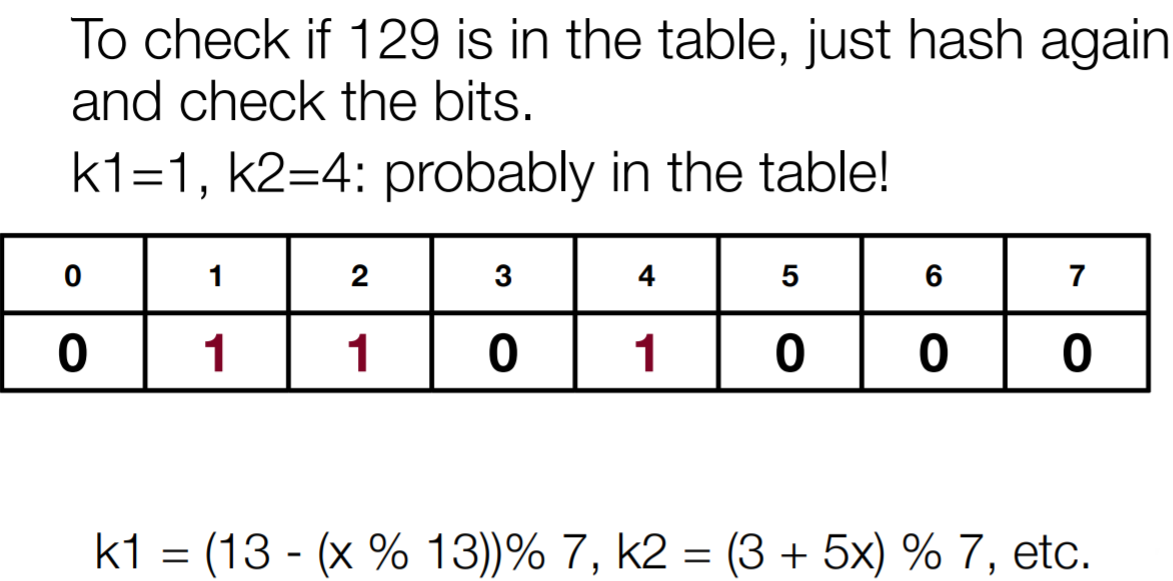
As we discussed above, Bloom Filter can generate some false positive results also which means that the element is deemed to be present but it is actually not present. To find out the probability of getting a false positive result in an array of k bits is: 1-(1/k).

The pseudocode for insertion of an element in the Bloom Filter is as follows:

function insert(element){
   hash1=hashfunction(element)% Size_Of_Array 
   hash2=hashfunction2(element)%Size_Of_Array
   array[hash1]=1;
   array[hash2]=1;
}

The pseudocode for searching an element in the Bloom Filter is as follows:

function search(element){
    hash1=h1(element)%Size_Of_Array;
    hash2=h2(element)%Size_Of_Array;
    if(array[hash1]==0 or array[hash2]==0){
        return false;
    }
    else{
        prob = (1.0 - ((1.0 - 1.0/Size_Of_Array)**(k*Query_Size))) ** k
    return "True";
    

Implementation of Bloom Filter

The following implementation is in Python 3 Programming Language which is a General-Purpose Programming Language:

import hashlib

class BloomFilter:
    def __init__(self, m, k):
        self.m = m
        self.k = k
        self.data = [0]*m
        self.n = 0
    def insert(self, element):
        if self.k == 1:
            hash1 = h1(element) % self.m
            self.data[hash1] = 1
        elif self.k == 2:
            hash1 = h1(element) % self.m
            hash2 = h2(element) % self.m
            self.data[hash1] = 1
            self.data[hash2] = 1
        self.n += 1
    def search(self, element):
        if self.k == 1:
            hash1 = h1(element) % self.m
            if self.data[hash1] == 0:
                return "Not in Bloom Filter"
        elif self.k == 2:
            hash1 = h1(element) % self.m
            hash2 = h2(element) % self.m
            if self.data[hash1] == 0 or self.data[hash2] == 0:
                return "Not in Bloom Filter"
        prob = (1.0 - ((1.0 - 1.0/self.m)**(self.k*self.n))) ** self.k
        return "Might be in Bloom Filter with false positive probability "+str(prob)

def h1(w):
    h = hashlib.md5(w)
    return hash(h.digest().encode('base64')[:6])%10

def h2(w):
    h = hashlib.sha256(w)
    return hash(h.digest().encode('base64')[:6])%10

Advantages of Bloom Filter

1. The Time Complexity associated with Bloom Filter Data Structure is O(k) during Insertion and Search Operation where k is the number of hash function that have been implemented.
2. The Space Complexity associated with Bloom Filter Data Structure is O(m) where m is the Size of the Array.
3. While a hash table uses only one hash function, Bloom Filter uses multiple Hash Functions to avoid collisions.

With this, you will have the complete knowledge of Bloom Filter. Enjoy.