
Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
Reading time: 35 minutes
Turing Machines can be used to express any computable algorithm, been this model recognized as equivalent to our concept of a modern computer. Both are considered general-purpose machine since they are capable of arithmetical logical operations and can be reprogramming to follow new instructions without changing the mechanism itself.
The mathematician Alan Turing was the inventor of this model, which he calls "a-machine" (automatic machine). With the invention, Turing was able to prove properties of the computation in general, he is considered today as the father of the theoretical computer science and artificial intelligence.
Definition
To define a formal model for an effective procedure, we have to consider some characteristics, which must be finitely describable and consist of discrete steps.
The model created by Alan Turing consists of: a finite control, an input tape divided into cells and a tape head that can read or write one cell of the tape at the time. Each cell can have written one of a restricted number of tape symbols. The tape itself it is admitted with an infinite length with most of its cells filled with the special symbol blank (B) that represented a no-input type.
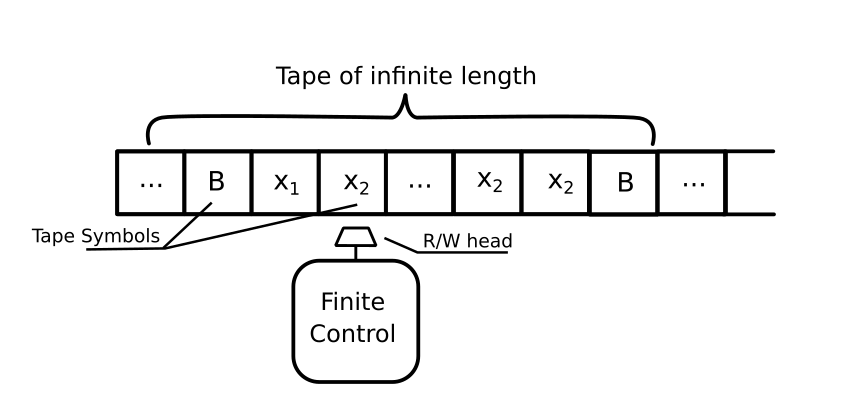
Every time the tape head scans a cell, the machine makes a move described in the following steps:
- The finite control examines the input and changes the state according to a transition function.
- The head prints any symbol of the machine alphabet (even the actual symbol) in the cell read before.
- Move the tape head left or right. The head can't remain stationary, always requiring a move.
For a formal notation, we can condense a Turing Machine to the expression:
M = (Q, Σ, Γ, δ, q0, B, F)
where the components can be described by:
- Q: The finite set of states of the finite control.
- Σ: The finite set of input symbols.
- Γ: The complete set of tape symbols, Σ is always a subset of Γ.
- δ: The transition function. Defines the next state assumed by the machine, the symbol to be written in the tape, and the direction which the head will moves.
- q0: The start state, a member of Q, where the finite control is found initially.
- B: the blank symbol. This symbol is in Γ but not in Σ.
- F: the set of final or accepting states, a subset of Q.
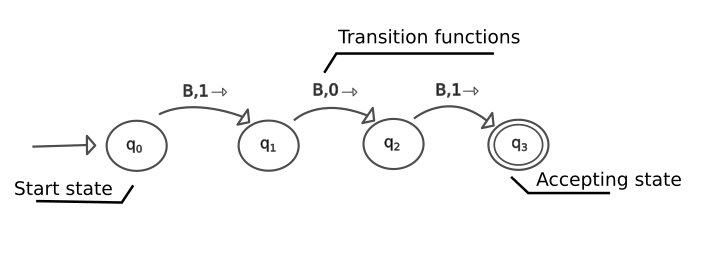
The image below illustrates another way to represent a Turing Machine. The circles are the set of states Q, and the arrows represent the transition functions together with the symbols attached to them. The first symbol indicates what type of the set of tape symbols will trigger that specific rule when reading on the tape, the second symbol show what will be written in the tape, replacing the current type. The third symbol indicates what side the head tape will move next. After the tape head moves to the next cell, the Finite Control changes the state for the state indicated by the last rule. If the machine reads a symbol on the tape and the actual state does not have a condition for that, the engine stops its algorithm, rejecting that input (the input don't match with the rules that the machine was built). The Turing Machine below writes a 101 sequence in a blank tape.
Sample
Imagine that you want to develop an automated system. Provided a binary input, the machine must answer if the input numbers of 1's and 0's are equals. This kind of problem can't be solved using ordinary automata, even using one with a stack system. For solve this puzzle, we need the ability to walk freely in each bit of the input, and a Turing Machine can provide us that.
There are many directions to solve this problem with a Turing Machine, an abordage it is to count the numbers of 0's and 1's in the data and identify those that have already be counted.
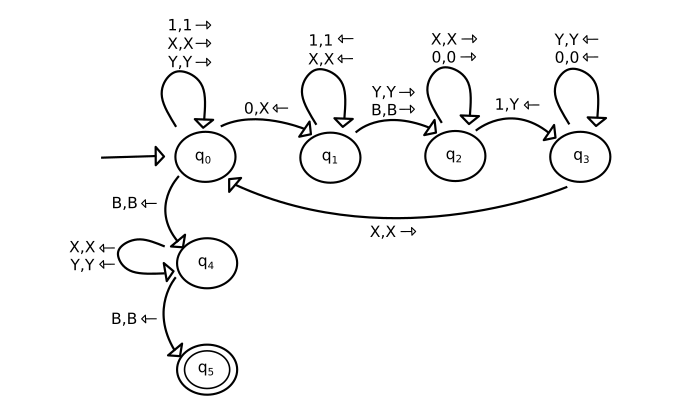
The illustration above show us a reasonable solution for this issue, being separated in the following actions to a more suitable comprehension of the machine. This solution is using the character X to mark any 0 already counted, and Y to any 1 counted.
- Walk in the tape to the right until finding a 0
- Change the 0 for an X
- Walk back in the tape until you find a blank symbol or a Y
- Walk to the right until finding a 1
- Change the 1 for Y
- Go back until finding an X
- Repeat until is over
If the machine was attempting to find the next 0 in the input and instead obtain a blank symbol, it will suppose that there is no more 0's to count. Thereon, it will return the tape head to the start, which will go into all the tape input one more time. If there are no more 1's symbols remaining in the tape, the machine goes to its final state and stops. That indicates an identical amount of 0's and 1's in the input.
Universal Turing Machine
Summing up, a Turing Machine is a construct able to execute algorithms that needs to store and to read data on a memory tape.
A Universal Turing Machine (UTM) otherwise, has a simple concept addition, it is a machine that can store in your tape instructions to emulate any other ordinary Turing Machine. With this ability, a UTM can be reprogrammed to make any task without just changing the data in your memory.
Applications
A Turing Machine brings the concept of a reprogrammable engine, capable of interpreting logical and mathematical operations and with a memory tape that can be read and written any moment by the mechanism control. This last sentence can be, additionally, the definition of a modern computing machine, the closest thing to a Universal Turing Machine these days.
