Maximum size square submatrix with all 1s

In this article, we have explored various ways to solve the problem of finding maximum size square submatrix with all 1s. This can be solved using Dynamic Programming.

Table of Contents
1) Introduction
2) Naive approach
3) Recursive approach
4) Dynamic Programming approach
5) Conclusion

Pre-requisites:

• Complete list of Dynamic Programming problems

1) Introduction

Given an m×n binary matrix.Find the size of largest square submatrix with all ones.

A binary matrix is that which consists of only 0s and 1s.

Let's understand the problem statement through a figure.

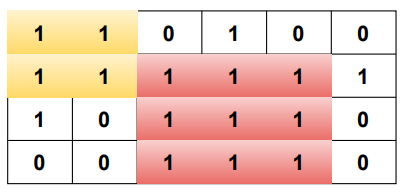
In the above matrix the submatrix with color 'yellow' is of size 2×2 and the submatrix with color 'red' is of size 3×3.

Hence, the largest square submatrix with all ones is of size 3 in the above case.

2) Naive approach

In this approach if a cell's value is 1,we incrementally check what can be the largest square submatrix(1×1 or 2×2 or 3×3....) with all ones exist considering each cell as the top-left corner of square submatrix.

Consider the following matrix

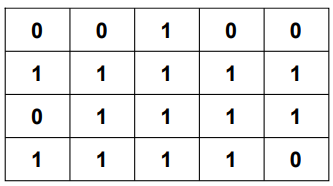
Considering cell colored with 'blue' as top-left corner top-left corner of square submatrix.

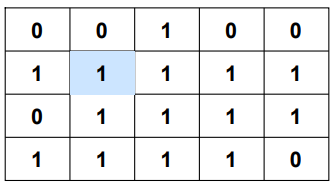
The algorithm works in the following way

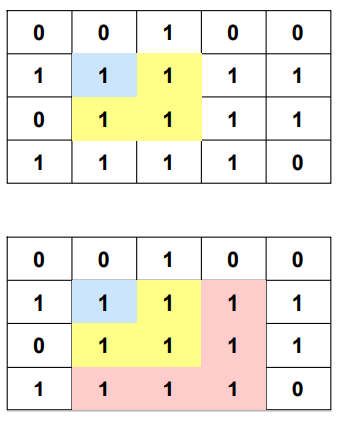
It checks whether a 1×1 submatrix then a 2×2 submatrix then a 3×3 submatrix and so on can be formed.

STEPS:

1. Go to each cell of the matrix
2. If the cell has 1, then find the largest square of 1s with the current cell as the top left corner.
   2.1. Simply traverse the cells incrementally one by one till a 0 is encountered
   2.2. Increase size of square to be checked and check newly added cells.
3. Keep track of the size of the largest square.

def maxSizeSquareSubMatrixWithAllOnes(matrix):
    rows,cols=len(matrix),len(matrix[0])
    res=0#store the maximum size of submatrix with all ones
    for i in range(rows):
        for j in range(cols):
            #initializing to next row and column to check
            #feasibility of submatrix as discussed
            rowCheck,colCheck=i+1,j+1
            #flag variable is used to stop checking
            #incase a zero is found
            flag=True 
            while rowCheck<rows and colCheck<cols and flag:
                #check for the next possible submatrix last column 
                #contains all ones or not
                for row in range(i,rowCheck+1):
                    if matrix[row][colCheck]==0:
                        flag=False#if any of the cell is 0 we can't proceed
                        break
                #check for the next possible submatrix last row 
                #contains all ones or not
                for col in range(j,colCheck+1):
                    if matrix[rowCheck][col]==0:
                        flag=False#if any of the cell is 0 we can't proceed
                        break
                if flag:#if we find a feasible submatrix
                    res=max(res,rowCheck-i+1)#update
                #increment to check next possible submatrix size
                rowCheck+=1 
                colCheck+=1
    return res
print(maxSizeSquareSubMatrixWithAllOnes(matrix = [
    [1,1,0,1,0,0],
    [1,1,1,1,1,1],
    [1,0,1,1,1,0],
    [0,0,1,1,1,0],
]))

Output:

3

Time complexity:

To visit each cell in the matrix it takes O(m×n) time complexity.
To calculate largest square submatrix with all ones we consider each cell as the top-left corner of a submatrix and check for the maximum size submatrix possible incrementally i.e.,1×1 , 2×2 , 3×3 and so on.This takes O(m×n) time complexity.

Hence overall it takes O(mn)×O(mn)=O((mn)²) , where m and n are the number of rows and columns of the given matrix respectively.

3) Recursive approach

This approach is similar to the above one but solving the method recursively.

STEPS:

1. Go to each cell of the matrix
2. If the cell has 1, then find the largest square of 1s with the current cell as the top left corner.
   2.1. Recursively traverse the cells to find the largest square of 1s till a 0 is encountered or position is not valid.
3. Keep track of the size of the largest square.

def maxSizeSquareSubMatrixWithAllOnes(matrix):
    rows,cols=len(matrix),len(matrix[0])
    res=0
    #function to check if a given position is valid
    def isValidPos(i,j):
        if i<0 or j<0 or i>=rows or j>=cols:
            return False
        return True
    def helper(i,j):
        if isValidPos(i,j)==False or matrix[i][j]==0:#if the position is not valid or the cell value is 0 nothing can be built from it
            return 0
        return 1+min(helper(i+1,j+1),min(helper(i+1,j),helper(i,j+1)))#recurrence relation
    for i in range(rows):
        for j in range(cols):
            res=max(res,helper(i,j))#for each cell in the matrix calculate the largest square submatrix with all ones with it as the top-left corner
    return res
print(maxSizeSquareSubMatrixWithAllOnes(matrix = [
    [1,1,0,1,0,0],
    [1,1,1,1,1,1],
    [1,0,1,1,1,0],
    [0,0,1,1,1,0],
]))

Output:

3

Time complexity:

To visit each cell in the matrix it takes O(m×n) time complexity.
For each cell calculate the matrix is traversed again recursively in three directions taking O(3^(m+n)) time complexity.
Hence overall it takes O(m×n×3^(m+n)), where m and n are the number of rows and columns of the given matrix respectively.

There'll be space overhead considering the recursion stack.

Consider the pictorial representation of recursion calls

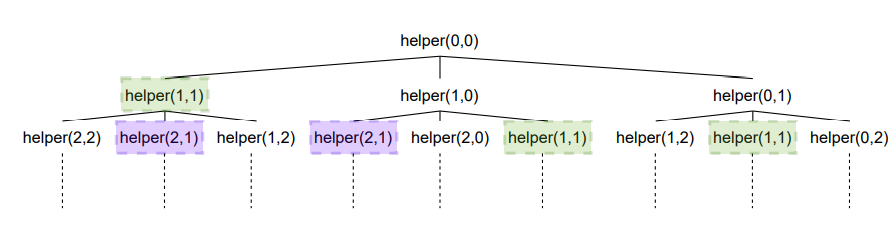
There are overlapping subproblems and also there is optimal substructure.Hence, the problem can be solved using Dynamic Programming.

4) Dynamic Programming approach

Here we'll consider each cell in the dp table as the bottom-right corner of a square submatrix.

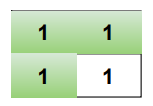
Consider a 2×2 matrix, it is said to contain all ones if the bottom-right corner is 1 along with each of top, left, and top-left cells are all 1s.

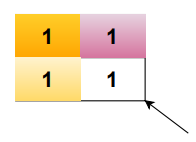
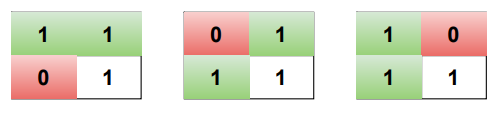
Consider a 3×3 matrix, it is said to contain all ones if the bottom-right corner is 1 along with each of top, left, and top-left all are bottom-right corners of some 2×2 sub-matrix.

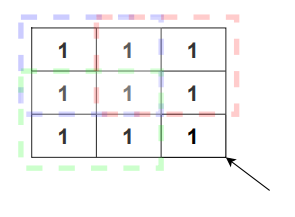
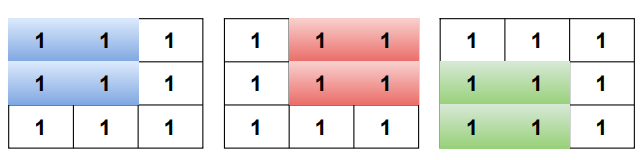
In general for any n×n matrix is said to contain all ones if the bottom-right corner is 1 along with each of top, left, and top-left all are bottom-right corners of some (n-1)×(n-1) sub-matrix.

In dp approach if the current cell is 1 we look for surrounding cells to know whether the size of the matrix can be increased or not.

The surrounding cells here are the top cell, the left cell and the top-left cell.

If all the surrounding cells are 1s then the size of square submatrix can be increased.

If any of the surrounding cells is 0 then the size of square submatrix does not get increased.

We store the maximum square submatrix size with bottom-right corner as given position (i,j) in the matrix in the dp table so that the values can be used for further computation.

DP Structure:

dp[i][j]=Size of largest square submatrix with all 1s having bottom-right corner as (i,j).

Base Case:

The first row and first column values of the dp table are copied as it from the matrix because if a cell is zero then it won't form any sub-matrix and even it is 1 the size of largest square sub-matrix ending with it is still 1.

If i=0 or j=0
  dp[i][j]=matrix[i][j]

DP equation:

If matrix[i][j]=0
  dp[i][j]=0
Else
  dp[i][j]=1+min(dp[i][j-1],dp[i-1][j-1],dp[i-1][j])

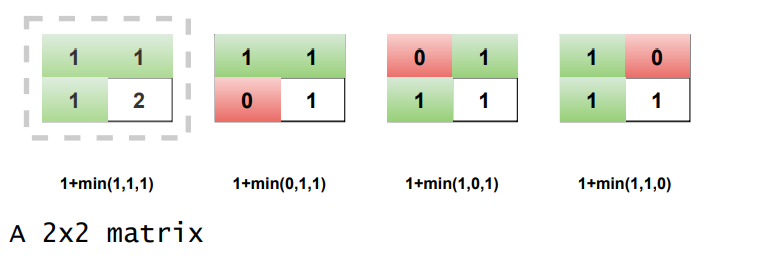
Let's take an example and build up the dp table

Consider the matrix

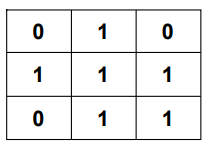
Building the dp table..

Fill the first row and column as it is from the matrix.

dp[1][1]= 1+min(dp[1][0],dp[0][0],dp[0][1])= 1+min(1,0,1)= 1+0= 1

dp[1][2]= 1+min(dp[1][1],dp[0][1],dp[0][2])= 1+min(1,1,0)= 1+0= 1

dp[2][1]= 1+min(dp[2][0],dp[1][0],dp[2][0])= 1+min(0,1,1)= 1+0= 1

dp[2][2]= 1+min(dp[2][1],dp[1][1],dp[1][2])= 1+min(1,1,1)= 1+1= 2

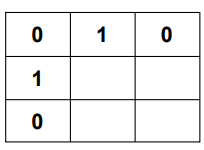
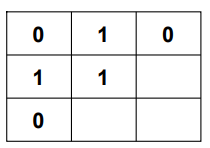
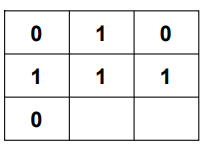
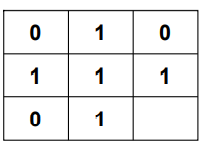
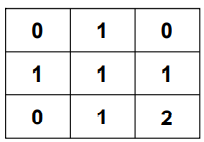
In the resultant dp matrix above the maximum value is 2.Hence, the maximum square sub-matrix with all 1s in the matrix is 2×2.

STEPS:

1. Let given matrix be mat with m rows and n columns.
2. Create a dp matrix with size that of mat i.e.,m×n.
3. Initialize the dp matrix with zeros.
4. Start traversing the dp matrix
   4.1. if the current cell (i,j) belongs to first row (i=0) or first column (j=0) then its value will same as that of in mat i.e.,dp[i][j]=mat[i][j].
   4.2. If the current cell (i,j) has value 0 in mat then its value will be 0 in dp too i.e., dp[i][j]=0.
   4.3. If the current cell (i,j) has value 1 in mat then its value in dp will be one plus minimum of the dp values of current cell's top,left,top-left cells i.e., dp[i][j]=1+min(dp[i][j-1],dp[i-1][j-1],dp[i-1][j]).
5. Keep track of the size of the largest square.

DP Implementation

def maxSizeSquareSubMatrixWithAllOnes(matrix):
    rows,cols=len(matrix),len(matrix[0])
    res=0
    dp=[[0 for j in range(cols)] for i in range(rows)]#initialize dp matrix with 0s
    for i in range(rows):
        for j in range(cols):
            if i==0 or j==0:
                dp[i][j]=matrix[i][j]#copying the first row and column as it is(Base Case)
            else:
                if matrix[i][j]==0:
                    dp[i][j]=0#if a cell is 0 then no submatrix can be formed using it
                else:
                    dp[i][j]=1+min(dp[i][j-1],dp[i-1][j-1],dp[i-1][j])#dp equation(recur)
                    res=max(res,dp[i][j])#update the maximum size each time
                
    return res
print(maxSizeSquareSubMatrixWithAllOnes(matrix = [
    [1,1,0,1,0,0],
    [1,1,1,1,1,1],
    [1,0,1,1,1,0],
    [0,0,1,1,1,0],
]))

3

5) Conclusion

Hence,for the given problem dynamic programming approach is the optimized one with time complexity of O(m×n) since the given matrix is traversed once and space complexity of O(m×n) since a dp matrix is used, where m and n are the number of rows and columns of the given matrix respectively.

With this article at OpenGenus, you must have the complete idea of solving the problem "Maximum size square submatrix with all 1s".