De Bruijn Sequences

In this article, we have explored De Bruijn Sequences and 3 algorithms to calculate De Bruijn Sequences using ideas like Hamiltonian Cycle, Euler's path.

Contents

1. Introduction
2. Method 1: Hamiltonian Cycle
3. Method 2: Euler's Path
4. Method 3: Algorithm

Introduction

Consider a problem where we are given a set A consisting of k numbers. Given an integer n, the objective is to find a sequence of numbers S such that every possible n - digit combination from A occurs exactly once in this sequence. Such a sequence is called a de Bruijn sequence. These sequences have been named after the Dutch mathematician Nicolaas de Bruijn, and find widespread applications in the fields of computing, robotics and DNA sequencing.

For example, if the given set consists of two numbers 1 and 2, and we are to make a de Bruijn sequence of combinations of length 3, the set of all possible combinations is {111, 112, 121, 122, 211, 212, 221, 222}. Hence, one possible de Bruijn sequence here would be 1112122211. There would be many other valid de Bruijn sequences of the same length. However, our focus lies more on finding the length of the de Bruijn sequence.

There exist multiple methods to obtain the de Bruijn sequence for a given set of k numbers and a given length n. We shall look into some of these methods in detail.

Method 1: Hamiltonian Path

This method uses the Hamiltonian cycle in order to solve the problem. A Hamiltonian cycle is a graph cycle (path) through the graph which visits each node of the graph exactly once.

Given a set of k numbers and a given length n, this method works as follows:

• Write down each possible combination of the given set as a vertex in the graph.
• Now, we connect one node to another node, if adding the last digit of the second node to the first node gives us a sequence of numbers in which two numbers are connected. For example, 111 and 112 can be connected in the previous example, since adding 2 to 111 gives 1112, where both 111 and 112 are present. Note that each node can be connected with itself too.
• The final step is to create a path through the created graph such that each vertex is visited exactly once. The solution will be the entire first node along with the last digit of all the succeeding nodes.

We consider the previous example. Here, we obtain the graph as follows:

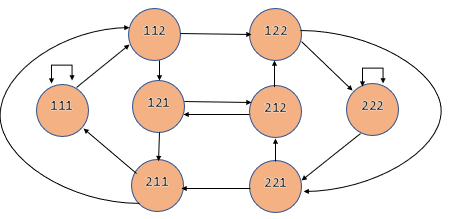
Hence, one example of a solution would be 1112221211. Another solution would be 1112122211. Note that any solution obtained with this algorithm would have the length of 10.

Although this method gives us the correct solution, as the size of the set A increases, so would the number of nodes in the graph, and hence it would become more complex to finish the graph and find an appropriate path. To be more precise, since this method relies on the Hamiltonian method for finding the solution, and the time complexity of this path is given by O(kⁿ 2^kn) which is not feasible as n and k increase. Hence, we try to find more efficient solutions for this problem.

Method 2: Euler's Path

This method uses Euler's path to solve the problem. An Euler's path is a graph cycle is a graph cycle which visits each edge of the graph exactly once.

Given a set of k numbers and a given length n, this method works as follows:

• Write down all possible combinations of length n - 1 as nodes of the graph.
• Now, connect the nodes in such as way that each node has k outgoing edges, each of which forms combinations with the nodes that it connects (of length n-1) in the same manner as in the Hamiltonian cycle.
• Now, create a path through the graph, going through each edge exactly once. The solution will be the entire first node along with the last digit of all the succeeding nodes.

For example, the graph for the given example would be as follows:

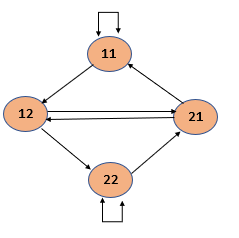
Hence, one solution would be 1112221211. Note that the length of the solution is 10, which is the same.

The implementation of the Euler's Path method using C++ is given below:

#include<iostream>
#include<string>
#include<vector>
#include<cmath>
#include<unordered_set>
using namespace std;

unordered_set<string> visited;
vector<int> indices;

void findpath(string beg, int k, string A)
{
  for(int i = 0; i < k; i++){
    string s = beg + A[i];
    if(visited.find(s) == visited.end()){
      visited.insert(s);
      findpath(s.substr(1), k, A);
      indices.push_back(i);
    }
  }
}

void Eulers_Path(int n, int k, string A)
{
  int len = pow(k, n);
  string S;
  string begNode = string(n-1, A[0]);
  findpath(begNode, k, A);
  for(int i = 0; i < len; i++)
  {
    S = S + A[indices[i]];
  }
  S = S + begNode;
  cout<<S;
}

int main()
{
  int n = 3, k = 3;
  string A = "123";
  Eulers_Path(n, k, A);
}

Here, the for loop inside the findpath method will run on average for kⁿ times, hence the time complexity of this method is given by O(kⁿ). Also, the space complexity is dependent on the number of edges, and is also hence given by O(kⁿ).

Although this solution is much more efficient than the Hamiltonian cycle, one can observe that as the size of the set increases, this method shall also become very complex.

Method 3: Algorithm

As the earlier two methods make the process of finding the correct solution extremely tedious in case of larger inputs, mathematicians have come up with an algorithm to find the de Bruijn sequence. Given a set of k digits and a number n, the algorithm is as follows:

• Start by writing all the combinations containing n digits, as well as the combinations of lengths which divide n. (For example, if n = 4, the combinations would be of length 1, 2, and 4).
• Now, order these combinations as if they are entries in a dictionary.
• Go through the elements of this ordering, crossing of elements which are periodic ,i.e., elements in which a particular sequence repeats itself (for example, 1212). Also cross of elements, which if rotated, forms an element already present in the list (for example, 3111 would be crossed off as 1113 would already be present in the list).
• Arrange all the elements that remain next to each other, and we obtain the required solution.

For example, consider the set of elements {1, 2, 3} and we are to make all the 3 digit combinations using the same.

Here, the list that we obtain, in dictionary order will be {1, 111, 112, 113, 121, 122, 123, 131, 132, 133, 2, 211, 212, 213, 221, 222, 223, 231, 232, 233, 3, 311, 312, 313, 321, 322, 323, 331, 332, 333}.

We now proceed by removing elements as stated by the algorithm. Hence, we shall obtain the set of elements as follows: {1, 112, 113, 122, 123, 132, 133, 2, 223, 233, 3}. Hence one of the possible solutions is 111211312212313213322232333.

Note that although this method might seem tedious, it can be generalized to find the solution for any input size. Since this method goes through all possible combinations, it's time complexity is also given by O(kⁿ). However, it is much easier to perform for larger outputs than the earlier two methods.

With this article at OpenGenus, you must have the complete idea of De Bruijn Sequences.