
Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
In this article, we will learn how to design and implement Quicksort in C++ Programming Language in detail.
Pre-requisites:
Definition:
Quick Sort is a sorting algorithm based on divide and conquer paradigm. It was first proposed by Tony Hoare in 1959 and is one of the most widely used sorting algorithms in computer science.
The main idea is to divide the array into two sub-parts and then further quick sort algorithm will be applied on these parts. This division of array takes place using a pivot element. The elements on the left side of the pivot should be smaller than the pivot element and the elements on the right side should be greater than the pivot element.
Algorithm:
Quicksort is a divide-and-conquer algorithm.
Steps to perform the quicksort algorithm:
- First, choose a pivot element. The pivot element can be the first element, last element, middle element or any random element of the array.
- Divide the array taking pivot as the partitioning point.
- The elements which are smaller than the pivot element are placed on the left side and the elements which are greater than the pivot element are placed on the right side of the pivot.
- The left and right sub-arrays are again partitioned by choosing the pivot elements for them. This process continues by recursively passing the sub-arrays to Quicksort.
- We will then combine the sub-arrays which are already sorted.
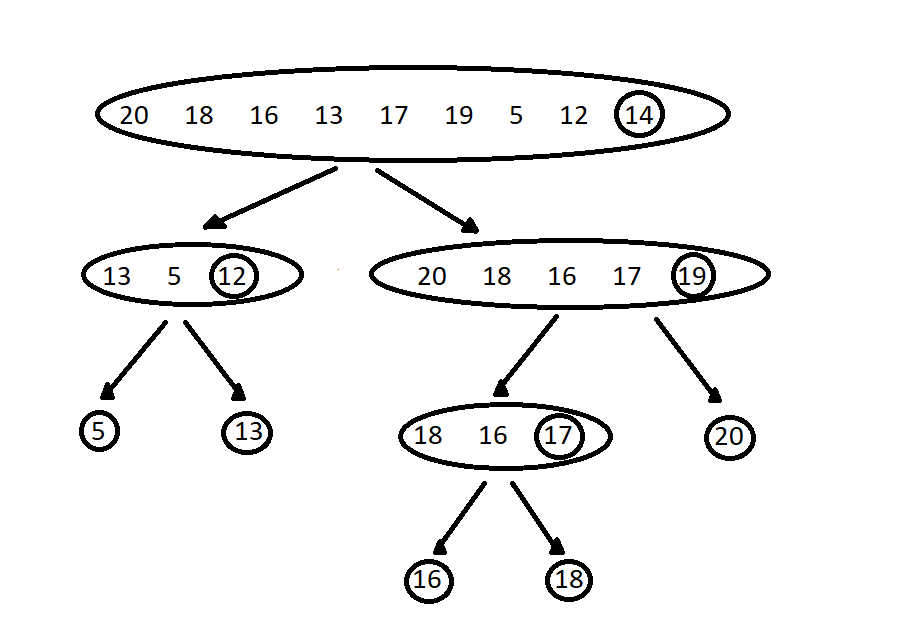
Figure: Partitioning of array around pivot element
Implementation of the Quicksort algorithm using Object-Oriented Programming(OOP):
Three private member functions - quickSort, partition, and swap are used to define the QuickSort class in this section. A public member function, sort calls the quickSort function to sort an array after getting an array and its size as arguments.
Following is the structure of QuickSort class:
class QuickSort {
public:
void sort(int arr[], int size) {
quickSort(arr, 0, size-1);
}
private:
void quickSort(...) {
// ...
}
void partition(...) {
// ...
}
void swap(...) {
// ...
}
}
From the point of user, we can use this class as follows:
QuickSort qSort;
qSort.sort(arr, n);
The Quicksort Algorithm is carried out using the recursive quickSort function. It calls the partition function to divide the sub-array around a pivot element, passing the array, the left and right indices of the sub-array to be sorted as arguments. After that, it repeatedly calls itself on the left and right sub-arrays.
The partition function divides the sub-array into two parts: elements smaller than the pivot on the left, and elements larger than the pivot on the right. The rightmost element in the sub-array is chosen as the pivot. The elements are rearranged using the swap function, and the pivot's index is returned.
The swap function is used to swap two elements in the array.
//Quick Sort Algorithm
#include<bits/stdc++.h>
using namespace std;
class QuickSort {
public:
void sort(int arr[], int size) {
quickSort(arr, 0, size-1);
}
private:
void quickSort(int arr[], int left, int right) {
if (left < right) {
int pivotIndex = partition(arr, left, right);
quickSort(arr, left, pivotIndex-1);
quickSort(arr, pivotIndex+1, right);
}
}
int partition(int arr[], int left, int right) {
int pivot = arr[right];
int l = left - 1;
for (int r = left; r < right; r++) {
if (arr[r] < pivot) {
l++;
swap(arr[l], arr[r]);
}
}
swap(arr[l+1], arr[right]);
return l+1;
}
void swap(int& p, int& q) {
int tmp = p;
p = q;
q = tmp;
}
};
int main(){
int n;
cin>>n;
int arr[n];
for(int i = 0;i < n;i++){
cin>>arr[i];
}
QuickSort qSort;
qSort.sort(arr, n);
for(int i = 0;i < n;i++){
cout<<arr[i]<<" ";
}
return 0;
}
Output:
7
23 12 54 28 37 98 31
12 23 28 31 37 54 98
Time Complexity:
Best Case Complexity - The best-case occurs in the quick sort when the pivot element is the middle element or the element which is close to the middle element. The best-case time complexity of quicksort is O(nlogn).
Average Case Complexity - It occurs when the array elements are neither arranged in ascending nor descending order. The average case time complexity of quicksort is O(nlogn).
Worst Case Complexity - The worst case occurs when the pivot element is either greatest or smallest element. The worst-case time complexity of quicksort is O(n^2).
Space Complexity:
Quicksort has an average space complexity of O(log n) and a worst-case complexity of O(n). As recursion is used by quicksort to sort the subarrays, more memory is needed to accommodate the function call stack. The number of times the array can be divided in half, which is logn for an array of size n, determines the maximum depth of the recursion tree. It denotes that quicksort's space complexity is typically O(log n). However, in the worst case situation, the partitioning strategy results in subarrays of size 1 and n-1 and the pivot element chosen is the least or largest member in the array. As a result, there are n levels in the recursive tree, one for each member in the array, and the space complexity becomes O(n).
