
Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
Tic Tac Toe is one of the most popular game which needs only two players to play it. This classic game is developed with almost every well-known programming language. In this article, the game is developed using Reinforcement Learning.
Introduction
A machine learning area that trains models or agents to act on their own to complete tasks is called reinforcement learning. This training method teaches the agent through rewarding it for any desired acts, and punishing it for undesired ones. Based on this reward or punishment, the agent learns to take the most efficient action.
A tic tac toe game is a classic two-player game where on a 3X3 board, one player can put 'X' symbol and the other can put 'O' symbol. The players can choose any box on the board as long as the box is empty. The players take turns to put the symbols in order to play. To win the game, one of them has to match three same symbols in a row, or a column, or a diagonal line.
For example,
|X|O| |
| |X| |
| |O|X|
Here, the 'X' player wins. The game is over when any player wins or the board is full. If no one wins, then the game is draw.
Project Description
In this project, we have trained one agent to learn from reward and punishment. For winning the game, the reward is +1, and for losing the punishment is -1. This agent will use the symbol 'X'.
We have used Q-learning method of reinforcement learning to train this player. Using this method, the agent can find the best move based on the current move in a specific environment. It takes the action that has the best possiblity of maximizing the reward. To learn more about Q-learning click here.
Another player with the symbol 'O', will randomly choose an empty box for the input. The game will reset when the one player wins or it is draw.
Start The Project
We begin by importing the necessary libraries.
import numpy as np
import random
import time
from tkinter import *
import matplotlib.pyplot as plt
from IPython import display
We use Tkinter library of Python for this project. Tkinter provides grid() method that will help with accessing the boxes on the board. Also, tkinter methods are used for updating the board values after each input.
Building X-Player
X-player can only use the 'X' symbol. At the beginning it chooses a random action, but as the game progresses it calculates the best move based on the rewards and punishments it gets.
class X_Agent:
def __init__(self):
self.epsilon = 0.1
self.lr = 0.001
self.state_history = []
def initialize_V(self, env, state_winner_triples):
# initialize V
# if agent wins, V(s) = 1
# if agent loses or draw V(s) = 0
# otherwise V(s) = 0.5
V = np.zeros(env.max_states)
for state, winner, gameOver in state_winner_triples:
if gameOver:
if winner == env.x:
state_value = 1
elif winner == env.o:
state_value = 1
else:
state_value = 0
else:
state_value = 0.5
V[state] = state_value
self.V = V
def set_symbol(self, symbol):
self.symbol = symbol
def reset_history(self):
self.state_history = []
def choose_random_action(self, env):
empty_moves = env.get_empty_moves()
# select randomly from possible moves
random_index_from_empty_moves = np.random.choice(len(empty_moves))
next_random_move = empty_moves[random_index_from_empty_moves]
return next_random_move
def choose_best_action_from_states(self, env):
next_best_move, best_state = env.get_next_best_move(self)
return next_best_move, best_state
We define the learning rate for the agent and a list to store the best states of the agent. These methods are used for checking empty boxes, choosing random actions, and choosing best actions. We initialize the state values according to the states of the game.
The symbol is set at the beginning of the class and it chooses a random box if the game is only starting, or the box that leads to winning.
def get_next_move(self, env):
next_best_move, best_state = None, None
random_number = np.random.rand() # will give a random float between 0 and 1
if random_number < self.epsilon:
# take a random action
next_best_move = self.choose_random_action(env)
else:
next_best_move, best_state = self.choose_best_action_from_states(env)
return next_best_move, best_state
def take_action(self, env):
selected_next_move, best_state = self.get_next_move(env)
# make next move
env.board[selected_next_move[0], selected_next_move[1]] = self.symbol
for i in self.state_history:
if best_state > self.state_history[i]:
self.state_history[i] = best_state
def update_state_history(self, state):
self.state_history.append(state)
def update(self, env):
# V(prev_state) = V(prev_state) + lr * ( V(next_state) - V(pre_state) ), where V(next_state) is reward if its most current state
reward = env.reward(self.symbol)
target = reward
for prev in reversed(self.state_history):
value = self.V[prev] + self.lr * (target - self.V[prev])
self.V[prev] = value
target = value
self.reset_history()
We use the reward, states of the game, states of the X-player to find the most efficient moves for the X-player. The epsilon value is used for reducing the randomness of the X-player. We update or reset the values as the games continues.
Building O-Player
The O-player only uses the 'O' symbol to play. This is called an agent, but it doesn't have the same functions as X-player. It chooses random values and finds an empty box for the input.
class O_Agent:
def set_symbol(self, symbol):
self.symbol = symbol
def take_action(self, env):
while True:
try:
i = random.randint(0,2)
j = random.randint(0,2)
if env.is_empty(i, j):
env.board[i, j] = self.symbol
break
else:
continue
except:
print("Please enter valid move")
The symbol is set as the X-player and a method chooses random values for rows and columns to put the symbol. This method keeps running until an empty spot is found.
Building The Environment
In this section, we create the gameboard, and use methods to perform other tasks. We assign +1 value to indicate X-player and -1 value to indicate O-player throughout the game. We also assign initial values for the winner, gameover, and maximum possible states for the game.
class Game():
def __init__(self):
self.board = np.zeros((3, 3)) # make an 2D array with zeros, zero means the box is empty
self.x = 1 # player 1
self.o = -1 # player 2
self.winner = None # initially there is no winner
self.gameOver = False # game is not gameOver initially
self.max_states = 3 ** (3 * 3) # =19683, total number of possible states for tic tac toe game
self.root = Tk()
self.root.title("Tic-Tac-Toe")
self.root.grid()
def is_empty(self, i, j):
return self.board[i, j] == 0
def reward(self, symbol):
collected_reward = 0
if self.game_over() and self.winner == symbol:
collected_reward = 1
else:
collected_reward = -1
return collected_reward
def is_draw(self):
is_draw = False
if self.gameOver and self.winner is None:
is_draw = True
return is_draw
At the beginning, the winner is set to None, and the gameOver is False. We also initialize Tkinter and the grid method here. We define methods to find empty boxes, check for draw, and assign reward or punishment to the player.
def get_state(self):
# returns the current state represented as an integer
# from 0...|S|-1 where S = set of all possible states ie |S| = 3^3, since each box can have three possible values 0(empty), x, o
# this is like finding the integer represented by a base-3 number
state = 0
loop_index = 0
for i in range(3):
for j in range(3):
if self.board[i, j] == self.x:
state_value = 1
elif self.board[i, j] == self.o:
state_value = 2
else:
state_value = 0 # empty
state += (3 ** loop_index) * state_value
loop_index += 1
return state
def game_over(self):
if self.gameOver:
return True # game is over
players = [self.x, self.o]
# check if there are any same symbols on rows side
for i in range(3):
for player in players:
if self.board[i].sum() == player * 3: # results will be 1+1+1 = 3 for player o and -1-1-1 = -3 for player x
self.winner = player
self.gameOver = True
return True # game is over
# check if there are any same symbols on columns side
for j in range(3):
for player in players:
if self.board[:, j].sum() == player * 3:
self.winner = player
self.gameOver = True
return True # game is over
# finally if there is no same symbols on either rows or columns we check on diagonal sides
for player in players:
# top-left -> bottom-right diagonal
# trace() function Return the sum along diagonals of the array
if self.board.trace() == player * 3:
self.winner = player
self.gameOver = True
return True # game is over
# top-right -> bottom-left diagonal
if np.fliplr(self.board).trace() == player * 3:
self.winner = player
self.gameOver = True
return True # game is over
# np.all() function Test whether all array elements along a given axis evaluate to True.
# self.board == 0 this will convert all positions of board to True or False, True if equal to 0 False if not
board_with_true_false = self.board == 0
if np.all(board_with_true_false == False):
# game is draw hence there is no winner
self.winner = None
self.gameOver = True
return True # game is over
# finally if game is not over
self.winner = None
return False
A method is defined to find the state of the agent. This is used to get the next best move for the agent. The game_over function checks if any player wins or the board is full. The players will win if they match 3 of their symbols diagonally, in the same row or in the same column. Otherwise, the game will go on until the players run out of empty spaces.
def get_empty_moves(self):
empty_moves = []
# we will be looping to all 9 boxes, and collecting possible moves which are empty
for i in range(3):
for j in range(3):
if self.is_empty(i, j): # check if this box is empty or not
empty_moves.append((i, j))
return empty_moves
def get_next_best_move(self, agent):
best_value = -1 # lets initialize with something lower
next_best_move = None
best_state = None
for i in range(3):
for j in range(3):
if self.is_empty(i, j):
# lets make this move and check what will be the state if we choose this move ie, (i, j) move, we we will revert it back after getting state
self.board[i, j] = agent.symbol
state = self.get_state()
self.board[i, j] = 0 # revert back to empty state ie actual state
if agent.V[state] > best_value:
best_value = agent.V[state]
best_state = state
next_best_move = (i, j)
return next_best_move, best_state
We create a list for the empty moves that are possible. To find the nest best move, we initialize something lower to the best state at the start. This value changes if the agent has found a better state. The next best move is the row and column number of that new best state.
def draw_board(self):
#making grid
self.squares = []
for i in range(3):
row = []
for j in range(3):
square_frame = Frame(
self.root,
bg='white',
width='80',
height='80',
)
square_frame.grid(row=i, column=j, padx=4, pady=4)
square = Label(self.root, bg='white', text=' ')
square.grid(row=i, column=j)
square_data = {"frame": square_frame, "number": square}
row.append(square_data)
self.squares.append(row)
def update_board(self):
self.draw_board()
for i in range(3):
for j in range(3):
if self.board[i, j] == self.x:
self.squares[i][j]["frame"].configure(bg="lightgrey")
self.squares[i][j]["number"].configure(
bg="white",
fg="black",
font=('Arial', 50),
text= 'X'
)
elif self.board[i, j] == self.o:
self.squares[i][j]["frame"].configure(bg="lightgrey")
self.squares[i][j]["number"].configure(
bg="white",
fg="black",
font=('Arial', 50),
text= 'O'
)
else:
self.squares[i][j]["frame"].configure(bg="white")
self.squares[i][j]["number"].configure(
bg="white",
fg="black",
font=('Arial', 50),
text= ' '
)
self.root.update_idletasks()
time.sleep(0.2)
These methods create the grid which is the gameboard and update values after every move. We delay 0.2 seconds to update the values. The boxes are configured with the fonts, the colors, and the values they should receive.
Get The Result
We define methods to plot the result as a graph and finding the state of the game, if the game is over or not, and the winner.
def plot(x_scores, o_scores):
display.clear_output(wait=True)
display.display(plt.gcf())
plt.clf()
plt.title('Training...')
plt.xlabel('Number of Games')
plt.ylabel('Score')
plt.plot(x_scores)
plt.plot(o_scores)
plt.ylim(ymin=0)
plt.text(len(x_scores)-1, x_scores[-1], str(x_scores[-1]))
plt.text(len(o_scores)-1, o_scores[-1], str(o_scores[-1]))
plt.show(block=False)
plt.pause(0.1)
def get_state_hash_and_winner(env, i=0, j=0):
# (i, j) refers to the next box on the board to permute, we need to try -1, 0, 1
results = []
for v in [0, env.x, env.o]:
env.board[i, j] = v # if board is empty, it should already be 0
if j == 2:
if i == 2:
state = env.get_state()
gameOver = env.game_over()
winner = env.winner
results.append((state, winner, gameOver))
else:
results += get_state_hash_and_winner(env, i + 1, 0)
else:
# increment j, i stays the same
results += get_state_hash_and_winner(env, i, j + 1)
return results
We plot the graph of the scores of each player. We compare the score of the X-agent with the random moves chosen by the O-player. We view the score with the number of games played by the players.
We loop through the board to see if it is full and if there is a winner or the game is draw. We store the state value, gameover value, and the winner in a list.
Print The Game
A method is used to change the players after each move. Also this method updates the board after each move.
The main function is finally run to call the necessary methods, objects and plotting the graph.
def play_game(x_agent, o_agent, env, print_board):
current_player = None # p1 will start the game always
# loop until the game is over
continue_game = True
while continue_game:
if current_player == x_agent:
current_player = o_agent
else:
current_player = x_agent
# current player makes his move
current_player.take_action(env)
# update state histories
if current_player == x_agent:
state = env.get_state()
x_agent.update_state_history(state) # p1 will be agent
# update value function for agent
x_agent.update(env)
if print_board:
env.update_board() # draw updated board again
if env.game_over():
continue_game = False
env.root.destroy()
def main():
print("Starting the game...")
x_score = 0
o_score = 0
plot_x_scores = []
plot_o_scores = []
# initialize empty environment
env = Game()
state_winner_triples = get_state_hash_and_winner(env)
x_agent = X_Agent()
x_agent.set_symbol(env.x)
x_agent.initialize_V(env, state_winner_triples)
o_agent = O_Agent()
o_agent.set_symbol(env.o)
total_game_played = 0
while True:
env = Game()
play_game(x_agent, o_agent, env=env, print_board=True)
total_game_played += 1
if env.winner == env.x:
x_score += 1
elif env.winner == env.o:
o_score += 1
print("Game: ", total_game_played, " X_Agent score: ", x_score, " O_Agent score: ", o_score)
plot_x_scores.append(x_score)
plot_o_scores.append(o_score)
plot(plot_x_scores, plot_o_scores)
if __name__ == '__main__':
main()
Results
The gameboard with a draw match

The blue line represents the trained agent X-player score and the orange line represents the O-player score which only chose random moves.
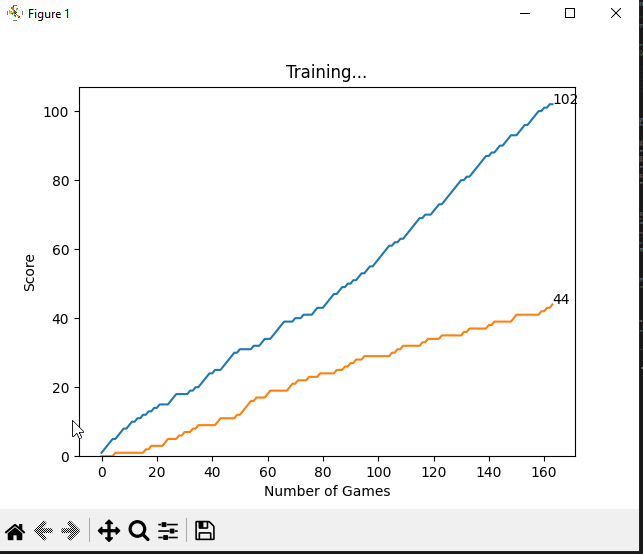
The scores after every game
With this article at OpenGenus, you must have the complete idea of Tic Tac Toe with Reinforcement Learning.
