
Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
Reading time: 30 minutes | Coding time: 15 minutes
In the range minimum query problem, we have to optimize two queries. One query is to find minimum value in a given range and the other query is to update an element at a given index. The update operation changes the minimum element in involved ranges which makes this a difficult problem.
In this article, we will sovle this problem Range Minimum query using square root decomposition which takes constant time O(1) for update and O(sqrt N) for range query. For the naive or brute force approach, go through this article at OpenGenus.
Problem Statement
Compute the minimum element in the given array within index ranges given by the user.
In this article we are going to explain the algorithms to solve range minimum queries .
We are given an array A[0....N-1].
The problem consist of two parts-:
-
Update(i,val): In this part we have to update an element at index i with val
-
Query(l,r): In this part we have to return the minimum value between index ‘l’ and ‘r’ inclusive
Example-:
Given an array A[] = {1,4,3,5,6,7}.
Tasks-:
- Compute the minimum element in the range (l,r)=(2,5).
- Update the value at index 3 to '0'.
- Compute the minimum element in the range (l,r)=(2,5).
Answers-:
- Minimum element in the index range (2,5) is '3'
- Minimum element in the index range (2,5) after updating element at index 3 is '0'
Square root decomposition
Basic Idea:
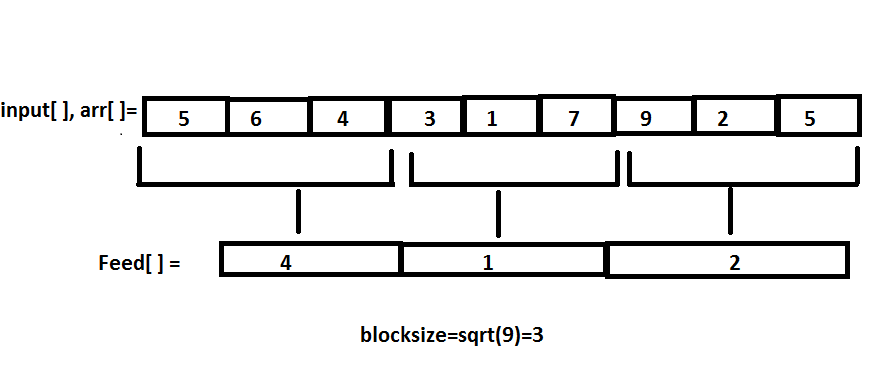
Divide the array of size 'n' into blocks of size ceil (sqrt[n]) and maintain an array say 'feed' to store the minimum element in each block and answer the queries accordingly.
We will be implementing the square root decomposition approach using three functions namely:
Build()- This function is used to make the 'feed' array with the help of which we will be able to solve the queries more efficiently.The feed array stores the minimum element in the blocks of size sqrt(n) .In this function we will also make the 'arr' which will be used as a substitute to 'input' array.
Pseudocode for build():
Build(A[],n,arr[],feed[])
{
blocksize=ceil(sqrt(n))
feed_pointer=-1
for(i from 0 to n)
arr[i]=A[i]
if(i%blocksize==0)
feed_pointer++
feed[feed_pointer]=min(A[i],A[i+1]...A[i+i%blocksize])
}
Query()- This function is implemented in three steps-
- 1 Finding the minimum in the first block that occurs in the given range.
- 2 Finding the minimum in the blocks that occur in between the index range (l,r).
- 3 Finding the minimum in the last block that occurs int the given range.
Pseudocode of query():
Query(l,r)
{
min_in_range=INT_MAX
//We compute this in three segments
//First segment
//Minimum in the first block in range
while(l<r and l%blocksize!=0 and l<r)
{
min_in_range=min(min_in_range,arr[l])
l++
}
//Second segment
//Minimum in the blocks lying between 'l' and 'r'
while(l+blocksize<=r)
{
min_in_range=min(min_in_range,feed[l/blocksize])
l+=blocksize
}
//Third segment
//Minimum in the last block lying in the range
while(l<=r)
{
min_in_range=min(min_in_range,arr[l])
l++
}
return min_in_range
}
Update()- This function is implemented by finding mathematically the 'feed' array index which considers the given index and comparing the value at that index with 'val'(new value given by the user).
Pseudocode of update():
Update(index,val)
{
feed_pointer=index/blocksize
feed[feed_pointer]=min(feed[feed_pointer],val)
arr[index]=val
}
A detailed working explanation can be understood through the Psuedo Code.
Time complexity:
Build-We simply traverse the whole array for making the 'feed' array therefore complexity is O(N)
Query-In the worst case if we have to iterate over sqrt(n) elements of 'feed' array (formally sqrt(n) 'blocks') to find the minimum element,the worst case complexity is O(sqrt(n)).
Update-We simply find the block in which the given index occurs and update the value at that particular index in O(1) complexity.
C++ Implementation
Following is the C++ implementation for this approach:
// Part of OpenGenus IQ
#include <bits/stdc++.h>
using namespace std;
void update(int index, int val, int n,int feed[],int arr[])
{
int blocksize = ceil(sqrt(n));
int feed_pointer = index / blocksize;
feed[feed_pointer]=min(val,feed[feed_pointer]);
arr[index] = val;
}
int query(int l, int r, int n, int feed[], int arr[])
{
int min_in_range=INT_MAX;
int blocksize = ceil(sqrt(n));
while (l<r && l%blocksize!=0 && l!=0)
{
// traversing first block in range
if(arr[l]<min_in_range)
{
min_in_range=arr[l];
}
l++;
}
while (l+blocksize <= r)
{
// traversing completely overlapped blocks in range
if(feed[l/blocksize]<min_in_range)
{
min_in_range= feed[l/blocksize];
}
l += blocksize;
}
while (l<=r)
{
// traversing last block in range
if(arr[l]<min_in_range)
{
min_in_range=arr[l];
}
l++;
}
return min_in_range;
}
void Build(int input[], int n,int arr[],int feed[])
{
int feed_pointer = -1;
// calculating size of block
int blocksize = ceil(sqrt(n));
// building the decomposed array
for (int i=0; i<n; i++)
{
arr[i] = input[i];
if (i%blocksize==0)
{
// entering next block
// incementing block pointer
feed_pointer++;
feed[feed_pointer]=arr[i];
}
feed[feed_pointer]=min(feed[feed_pointer],arr[i]);
}
}
int main()
{
int input[] = {8, 5, 12, 4, 6, 1, 14 , 7, 7, 10};
int n = sizeof(input)/sizeof(input[0]);
int arr[n],feed[n];
Build(input, n, arr,feed);
cout << "query(7,9) : Before update" <<"\t"<< query(7, 9,n,feed,arr) << endl;
update(8, 0,n,feed,arr); //update 8 index by 0
cout << "query(7,9) : After update" <<"\t"<< query(7, 9,n,feed,arr) << endl;
return 0;
}
Output
query(7,9) : Before update 7
query(7,9) : After update 0
Different ways to solve this problem:
There are different ways to solve this problem:
-
- query in O(N)
- update in O(1)
-
- query: O(square-root of N)
- update: O(1)
-
- query: O(log N)
- update: O(log N)
-
- query: O(log N)
- update: O(N log N)
-
- query: O(1)
- update: O(N log N)
-
Cartesian Tree and Farach-Colton and Bender algorithm
- query: O(1)
- update: O(N)
With this, you should have a strong basic knowledge of this problem. We will work over improving this with other efficient approaches in our other articles. Enjoy.
