
Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
Reading time: 45 minutes | Coding time: 20 minutes
A skip list is a data structure that is used for storing a sorted list of items with a help of hierarchy of linked lists that connect increasingly sparse subsequences of the items. A skip list allows the process of item look up in efficient manner. The skip list data structure skips over many of the items of the full list in one step, that’s why it is known as skip list.
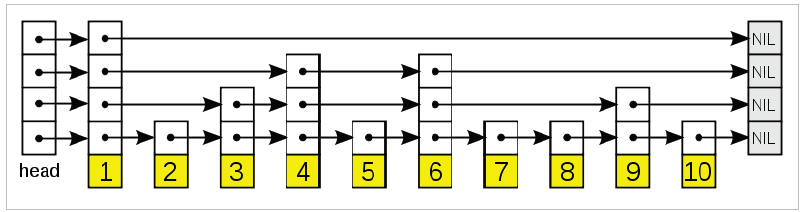
In short, skip lists are a linked list like structure which allows for fast search. It consists of a base list holding the elements, together with a tower of lists maintaining a linked hierarchy of subsequences, each skipping over fewer elements.
Description
A skip list is built in layers:
- The bottom layer is an ordinary ordered linked list.
- Each higher layer acts as an "express lane" for the lists below, where an element in layer i appears in layer i+1 with some fixed probability p (two commonly-used values for p are 1/2 or 1/4).
On average, each element appears in 1/(1-p) lists, and the tallest element (usually a special head element at the front of the skip list) appears log1/pn in lists.
A search for a target element begins at the head element in the top list, and proceeds horizontally until the current element is greater than or equal to the target.
If the current element is equal to the target, it has been found.
If the current element is greater than the target, the procedure is repeated after returning to the previous element and log1/pn/p which is 0(logn) where p is a constant. By choosing different values of p, it is possible to trade search costs against storage costs.
Working
We create multiple layers so that we can skip some nodes.
See the following example list with 16 nodes and two layers. The upper layer works as an express lane which connects only main outer stations, and the lower layer works as a normal lane which connects every station. Suppose we want to search for 50, we start from first node of “express lane” and keep moving on “express lane” till we find a node whose next is greater than 50. Once we find such a node (30 is the node in following example) on “express lane”, we move to “normal lane” using pointer from this node, and linearly search for 50 on “normal lane”. In following example, we start from 30 on “normal lane” and with linear search, we find 50.

Basic Operations
Following are the Operations Performed on Skip list:-
- Insertion Operation : To Insert any element in a list
- Search Operation : To Search any element in a list
- Deletion Operation : To Delete any element from a list
Insertion Operation
Before we start inserting the elements in the skip list we need to decide the nodes level.Each element in the list is represented by a node, the level of the node is chosen randomly while insertion in the list. Level does not depend on the number of elements in the node. The level for node is decided by the following algorithm –
randomLevel()
lvl := 1
//random() that returns a random value in [0...1)
while random() < p and lvl < MaxLevel do
lvl := lvl + 1
return lvl
MaxLevel is the upper bound on number of levels in the skip list. It can be determined as – L(N) = logp/2(N). Above algorithm assure that random level will never be greater than MaxLevel. Here p is the fraction of the nodes with level i pointers also having level i+1 pointers and N is the number of nodes in the list.
Node Structure :- Each node carries a key and a forward array carrying pointers to nodes of a different level. A level i node carries i forward pointers indexed through 0 to i.
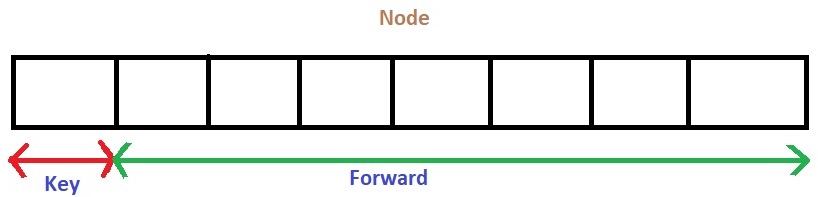
We will start from highest level in the list and compare key of next node of the current node with the key to be inserted. Basic idea is:
- Key of next node is less than key to be inserted then we keep on moving forward on the same level
- Key of next node is greater than the key to be inserted then we store the pointer to current node i at update[i] and move one level down and continue our search.
Pseudocode For Insertion
Insert(list, searchKey)
local update[0...MaxLevel+1]
x := list -> header
for i := list -> level downto 0 do
while x -> forward[i] -> key forward[i]
update[i] := x
x := x -> forward[0]
lvl := randomLevel()
if lvl > list -> level then
for i := list -> level + 1 to lvl do
update[i] := list -> header
list -> level := lvl
x := makeNode(lvl, searchKey, value)
for i := 0 to level do
x -> forward[i] := update[i] -> forward[i]
update[i] -> forward[i] := x
- Here update[i] holds the pointer to node at level i from which we moved down to level i-1 and pointer of node left to insertion position at level 0.
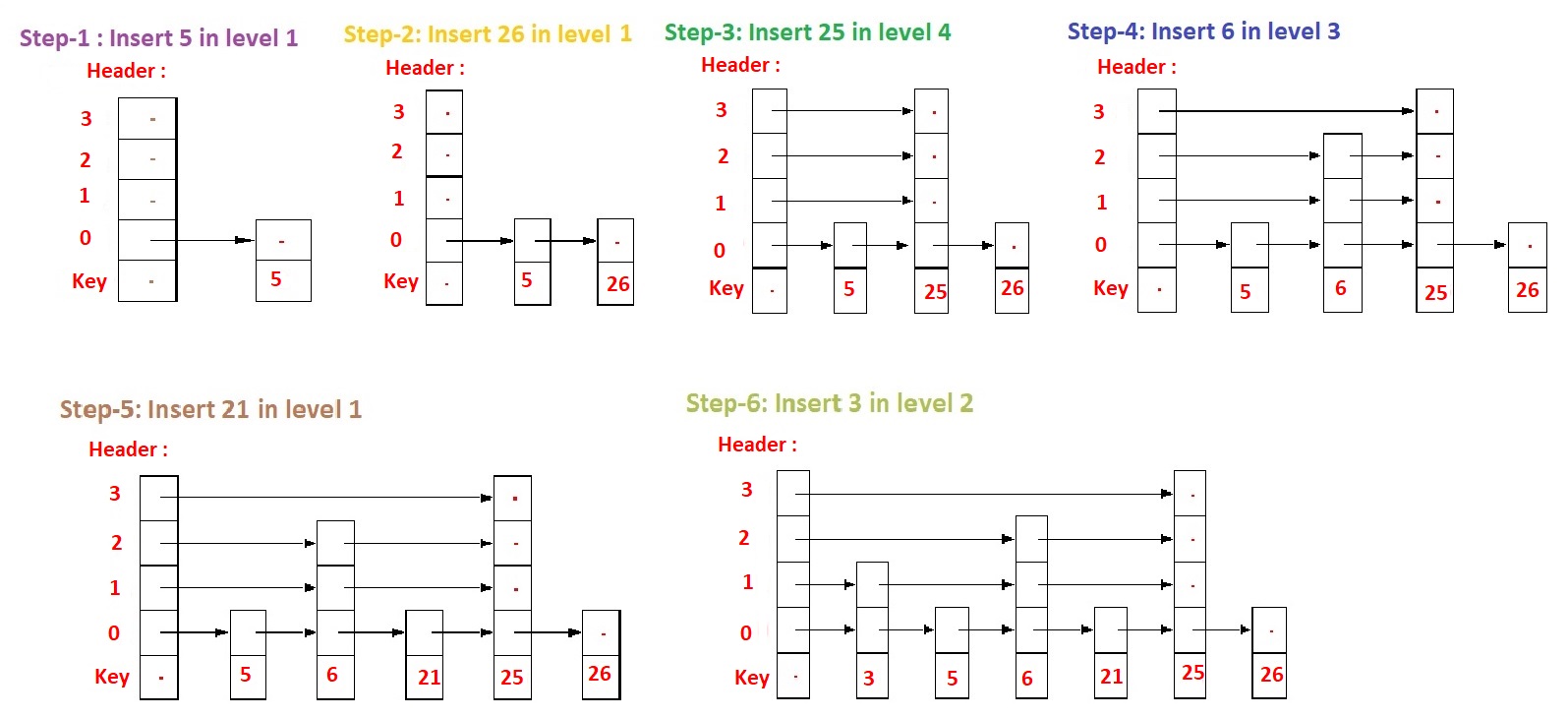
Example
Starting with an empty Skip list with MAXLEVEL 4, Suppose we want to insert these following keys with their "Randomly Generated Levels":
5 with level 1, 26 with level 1, 25 with level 4, 6 with level 3, 21 with level 1, 3 with level 2, 22 with level 2 .
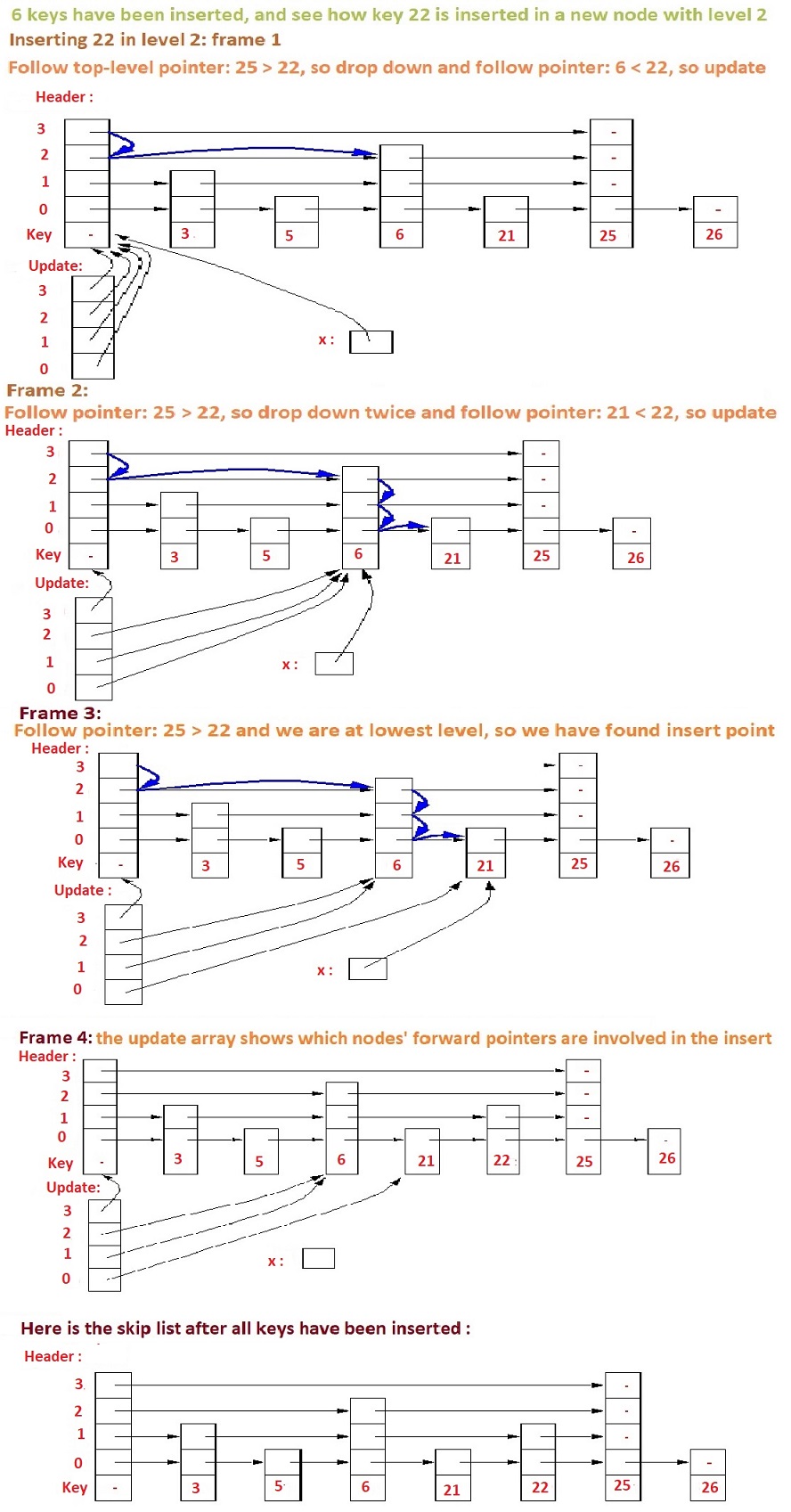
Now, at Step-7 where we need to insert 22 in level 2 we need to go through some following details:
The insert algorithm maintains two local variables(besides the skip list header):
- X, a pointer which points to a node whose forward pointers point to nodes whose key we are currently comparing to the key we want to insert this lets us quickly compare keys, and follow forward pointers
- update, an array of node pointers which point to nodes whose forward pointers may need to be updated to point to the newly inserted node , if the new node is inserted in the list just before the node X points to this lets us quickly update all the pointers necessary to splice in the new node
Searching Operation
Searching an element is very similar to approach for searching a spot for inserting an element in Skip list. The basic idea is if –
1. Key of next node is less than search key then we keep on moving forward on the same level.
2. Key of next node is greater than the key to be inserted then we store the pointer to current node i at update[i] and move one level down and continue our search.
- At the lowest level (0), if the element next to the rightmost element (update[0]) has key equal to the search key, then we have found key otherwise failure.
Pseudocode For Searching:
Search(list, searchKey)
x := list -> header
-- loop invariant: x -> key level downto 0 do
while x -> forward[i] -> key forward[i]
x := x -> forward[0]
if x -> key = searchKey then return x -> value
else return failure
Example Of Searching
Consider this example where we want to search for key 17-
Now to search for key in a skip list we will follow the steps of our Pseudocode.
Here, the idea is that we will compare the key values of every node with our search key (ie 17). if the key of next node is greater than our key 17 then we keep on moving on that same level otherwise we store the pointer to current node i at update[i] and move one level down and continue our search. Here, we will stop at which the key of next node is 19 (ie 17 < 19) and store pointer of that node.

Deletion Operation
Deletion of an element k is preceded by locating element in the Skip list using above mentioned search algorithm. Once the element is located, rearrangement of pointers is done to remove element from list just like we do in singly linked list. We start from lowest level and do rearrangement until element next to update[i] is not k.After deletion of element there could be levels with no elements, so we will remove these levels as well by decrementing the level of Skip list.
Pseudocode For Deletion
Delete(list, searchKey)
local update[0..MaxLevel+1]
x := list -> header
for i := list -> level downto 0 do
while x -> forward[i] -> key forward[i]
update[i] := x
x := x -> forward[0]
if x -> key = searchKey then
for i := 0 to list -> level do
if update[i] -> forward[i] ≠ x then break
update[i] -> forward[i] := x -> forward[i]
free(x)
while list -> level > 0 and list -> header -> forward[list -> level] = NIL do
list -> level := list -> level – 1
Example of deletion
Consider this example where we want to delete element 6 –
Deletion of an element 6 is preceded by locating this element 6 in the Skip list using above mentioned search algorithm. Once 6 is located, rearrangement of pointers is done to remove 6 from list just like we do in singly linked list.
First we must find the preceding node ie 3 and identify the nodes whose pointers may need to be reset. Next we must reset the pointers to the targeted node "around" it (ie 7), and finally we deallocate the targeted node ie 3.
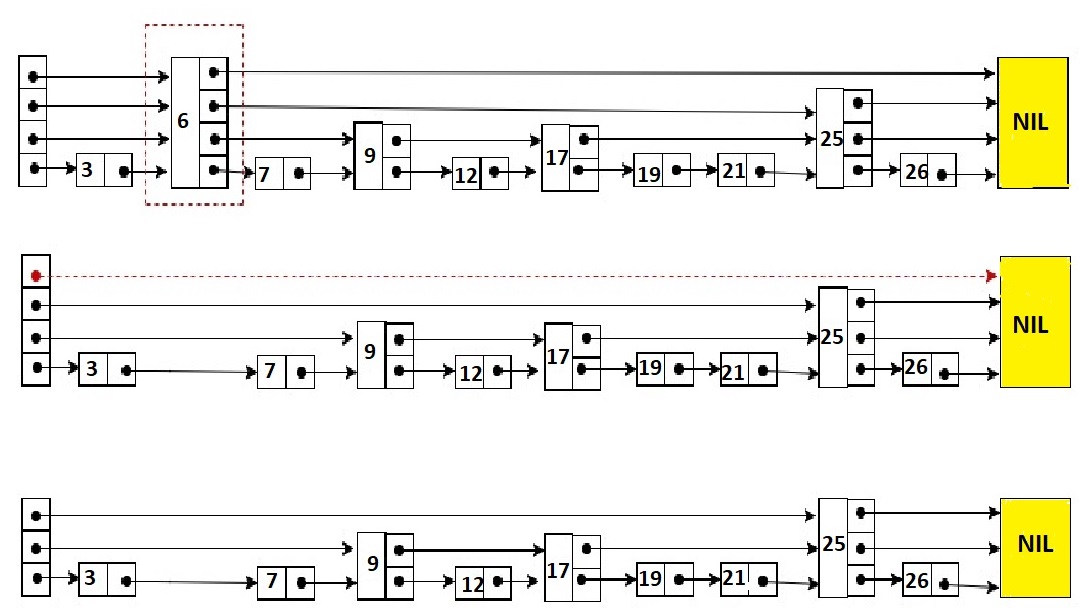
- Here at level 3, there is no element (arrow in red) after deleting element 6. So we will decrement level of skip list by 1.
Complexity
Time Complexity:-
| Operations | Average Case | Worst Case |
|---|---|---|
| Search | O(logn) |
O(n) |
| Insertion | O(logn) |
O(n) |
| Deletion | O(logn) |
O(n) |
Space Complexity : O(N log N)
A skip list is built in layers. The bottom layer is an ordinary ordered linked list. Each higher layer acts as an "express lane" for the lists below, where an element in layer i appears in layer i+1 with some fixed probability p (two commonly used values for p are 1/2 or 1/4). On average, each element appears in 1/(1-p) lists, and the tallest element (usually a special head element at the front of the skip list) in all the lists. The skip list contains log1/pn lists.
A search for a target element begins at the head element in the top list, and proceeds horizontally until the current element is greater than or equal to the target. If the current element is equal to the target, it has been found. If the current element is greater than the target, or the search reaches the end of the linked list, the procedure is repeated after returning to the previous element and dropping down vertically to the next lower list. The expected number of steps in each linked list is at most 1/p, which can be seen by tracing the search path backwards from the target until reaching an element that appears in the next higher list or reaching the beginning of the current list. Therefore, the total expected cost of a search is 1/p(log 1/pn) which is O(log n) when p is a constant.
The Search, insert, and delete operations on ordinary binary search trees are efficient, O(log n), when the input data is random; but less efficient, O(n), when the input data are ordered. Skip List performance for these same operations and for any data set is about as good as that of randomly-built binary search trees - namely O(log n)
In an ordinary sorted linked list, Search, insert, and delete are in O(n) because the list must be scanned node-by-node from the head to find the relevant node. If somehow we could scan down the list in bigger steps (skip down, as it were), we would reduce the cost of scanning. This is the fundamental idea behind Skip Lists.
We speak of a Skip List node having levels, one level per forward reference. The number of levels in a node is called the size of the node.
In an ordinary sorted list, insert, delete, and search operations require sequential traversal of the list. This results in O(n) performance per operation. Skip Lists allow intermediate nodes in the list to be skipped during a traversal - resulting in an expected performance of O(log n) per operation.
Implementation
- C++
C++
# include<bits/stdc++.h>
using namespace std;
// Class to implement node
class Node
{
public:
int key;
// Array to hold pointers to node of different level
Node **forward;
Node(int, int);
};
Node::Node(int key, int level)
{ this->key = key;
// Allocate memory to forward
forward = new Node*[level+1];
// Fill forward array with 0(NULL)
memset(forward, 0, sizeof(Node*)*(level+1));
};
// Class for Skip list
class SkipList
{
// Maximum level for this skip list
int MAXLVL;
// P is the fraction of the nodes with level
// i pointers also having level i+1 pointers
float P;
// current level of skip list
int level;
// pointer to header node
Node *header;
public:
SkipList(int, float);
int randomLevel();
Node* createNode(int, int);
void insertElement(int);
void deleteElement(int);
void searchElement(int);
void displayList();
};
SkipList::SkipList(int MAXLVL, float P)
{ this->MAXLVL = MAXLVL;
this->P = P;
level = 0;
// create header node and initialize key to -1
header = new Node(-1, MAXLVL);
};
// create random level for node
int SkipList::randomLevel()
{
float r = (float)rand()/RAND_MAX;
int lvl = 0;
while(r < P && lvl < MAXLVL)
{ lvl++;
r = (float)rand()/RAND_MAX;
}
return lvl;
};
// create new node
Node* SkipList::createNode(int key, int level)
{
Node *n = new Node(key, level);
return n;
};
// Insert given key in skip list
void SkipList::insertElement(int key)
{
Node *current = header;
// create update array and initialize it
Node *update[MAXLVL+1];
memset(update, 0, sizeof(Node*)*(MAXLVL+1));
for(int i = level; i >= 0; i--)
{
while(current->forward[i] != NULL && current->forward[i]->key < key)
current = current->forward[i];
update[i] = current;
}
current = current->forward[0];
if (current == NULL || current->key != key)
{ // Generate a random level for node
int rlevel = randomLevel();
if(rlevel > level)
{
for(int i=level+1;i<rlevel+1;i++)
update[i] = header;
// Update the list current level
level = rlevel;
}
// create new node with random level generated
Node* n = createNode(key, rlevel);
// insert node by rearranging pointers
for(int i=0;i<=rlevel;i++)
{ n->forward[i] = update[i]->forward[i];
update[i]->forward[i] = n;
}
cout<<"Successfully Inserted key "<<key<<"\n";
}
};
// Delete element from skip list
void SkipList::deleteElement(int key)
{
Node *current = header;
// create update array and initialize it
Node *update[MAXLVL+1];
memset(update, 0, sizeof(Node*)*(MAXLVL+1));
for(int i = level; i >= 0; i--)
{
while(current->forward[i] != NULL &¤t->forward[i]->key < key)
current = current->forward[i];
update[i] = current;
}
// If current node is target node
if(current != NULL and current->key == key)
{
for(int i=0;i<=level;i++)
{ if(update[i]->forward[i] != current)
break;
update[i]->forward[i] = current->forward[i];
}
// Remove levels having no elements
while(level>0 && header->forward[level] == 0)
level--;
cout<<"Successfully deleted key "<<key<<"\n";
}
};
// Search for element in skip list
void SkipList::searchElement(int key)
{
Node *current = header;
for(int i = level; i >= 0; i--)
{
while(current->forward[i] && current->forward[i]->key < key)
current = current->forward[i];
}
current = current->forward[0];
// If current node have key equal to
// search key, we have found our target node
if(current and current->key == key)
cout<<"Found key: "<<key<<"\n";
};
// Display skip list level wise
void SkipList::displayList()
{ cout<<"\n*****Skip List*****"<<"\n";
for(int i=0;i<=level;i++)
{ Node *node = header->forward[i];
cout<<"Level "<<i<<": ";
while(node != NULL)
{ cout<<node->key<<" ";
node = node->forward[i];
}
cout<<"\n";
}
};
// Driver to test above code
int main()
{ // Seed random number generator
srand((unsigned)time(0));
// create SkipList object with MAXLVL and P
SkipList lst(3, 0.5);
lst.insertElement(3);
lst.insertElement(6);
lst.insertElement(7);
lst.insertElement(9);
lst.insertElement(12);
lst.insertElement(19);
lst.insertElement(17);
lst.insertElement(26);
lst.insertElement(21);
lst.insertElement(25);
lst.displayList();
//Search for node 19
lst.searchElement(19);
//Delete node 19
lst.deleteElement(19);
lst.displayList();
}
Advantages
- Skip lists perform very well on rapid insertions because there are no rotations or reallocations.
- They’re simpler to implement than both self-balancing binary search trees and hash tables.
- You can retrieve the next element in constant time (compare to logarithmic time for inorder traversal for BSTs and linear time in hash tables).
- The algorithms can easily be modified to a more specialized structure (like segment or range “trees”, indexable skip lists, or keyed priority queues).
- Lock-free shared Skip List Data structures implement distributed objects without the use of mutual exclusion, thus providing robustness and reliability.
- It does well in persistent (slow) storage (often even better than AVL and EH).
Disadvantges
- skip lists take more space than a balanced tree
- skip lists are not cache friendly because they don't optimize locality of reference i.e. related elements tend to stay far apart and not on the same page.
- lack of available implementations. There are far more optimized tree implementations than skip lists.
Applications
List of applications and frameworks that use skip lists:
- Skip list are used in distributed applications. In distributed systems, the nodes of skip list represents the computer systems and pointers represent network connection.
- Skip list are used for implementing highly scalable concurrent priority queues with less lock contention (struggle for having a lock on a data item).
- QMap template class of Qt that provides a dictionary.
- skipdb is an open-source database format using ordered key/value pairs.
- Running Median using an Indexable Skiplist is a Python implementation of a skiplist augmented by link widths to make the structure indexable (giving fast access to the nth item). The indexable skiplist is used to efficiently solve the running median problem (recomputing medians and quartiles as values are added and removed from a large sliding window).
