
Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
In this article, we have explored an algorithm to sort a stack using another stack that is by using stack operations like push and pop only. The time complexity of this approach is O(N^2) and space complexity is O(N).
Stack : It is a linear data structure which follows a particular order in which the operations are performed. The order may be LIFO(Last In First Out) or FILO(First In Last Out).
Mainly the following three basic operations are performed in the stack:
Push: Adds an item in the stack. If the stack is full, then it is said to be an Overflow condition.
Pop: Removes an item from the stack. The items are popped in the reversed order in which they are pushed. If the stack is empty, then it is said to be an Underflow condition.
Peek or Top: Returns top element of stack.
isEmpty: Returns true if stack is empty, else false.
A typical example how stack push and pop operation is done is given below :
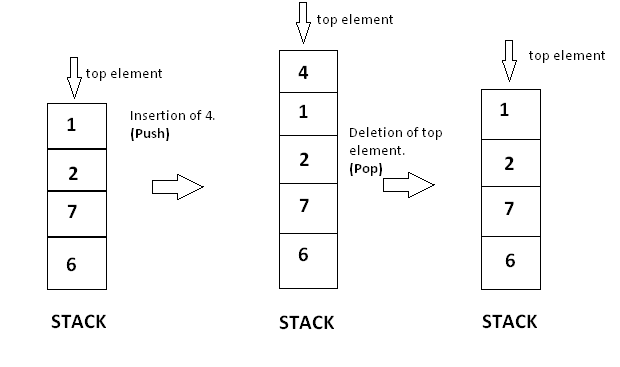
Sorting : Arranging the element into ascending or descending order is called as sorting it can be done in numerous ways but here we are doing it with the help of another stack.
PROBLEM
we have to perform sorting on a stack using another stack like it is done in the following example :-
Input : [7,3,29,2,1,14,5]
Output : [1,2,3,5,7,14,29]
Input : [3, 10, 1, 4, 2, 8]
Output : [1, 2, 3, 4, 8,10]
NOTE - We have to take only one stack because of space complexity, so we will learn optimised and the best approach for this question.
Approach :
let's dive into the best and optimised approach where we are going to use the extra constant variable called as temp and will use only one another stack.
We will put the largest element at the top of the stack and smallest at the bottom- Ascending Order.
we have to take two stacks :-
- input_stack
- sorted_stack
We can take n number of constant variables because we don't have any boundations on taking the variable number
- temp variable
ALGORITHM
- Create a temporary stack say sorted_stack.
- While input_stack is NOT empty do this:
- Pop an element from input_stack call it as temp
- while sorted_stack is NOT empty and top of sorted_stack is greater than temp, pop from sorted_stack and push it to the input_stack
- push temp in sorted_stack
- The sorted numbers are in sorted_stack.
At the intial step our input of elements will be added to the input_stack and sorted_stack will be empty and temp variable is also empty .
input_stack - [4, 1, 7, 9]
sorted_stack - [ ]
temp -
input_stack: [4, 7, 1, 9]
// pop top element of input_stack i.e 9 and store in temp variable
temp: 9
// push into sorted_stack
input_stack: [4, 7, 1 ]
sorted_stack: [9]
// pop next element from input_stack and store in temp
temp: 1
// compare temp element with top of stack element, if temp is less than top element of sorted_stack, then pop it and push it again in the input_stack
temp < 9
input_stack: [4, 7, 9]
sorted_stack: [1]
// pop next element from input_stack and store in temp
temp:9
//compare the temp with top element as it is greater so push it in sorted_stack
temp > 1
input_stack: [4, 7 ]
sorted_stack: [1, 9 ]
// pop next element from input_stack and store in temp
temp: 7
// compare temp with top element as temp is less so pop 9 and push 7 in the sorted_stack
temp < 9
input_stack: [4, 9]
sorted_stack: [1, 7]
// pop next element from input_stack and store in temp
temp: 9
//compare the temp variable as now temp is greater than top elementt of stack so push 9 in the stack
temp > 7
input_stack: [4 ]
sorted_stack: [1, 7, 9]
// pop next element from input_stack and store in temp
temp: 4
// compare temp with top element as it is less so pop 9 and then 7 from sorted_stack and push 4 in the sorted_stack
temp < 9
input_stack: [9, 7]
sorted_stack: [1, 4]
// pop next element from input_stack and store in temp
temp: 7
// compare temp with top element as it is less so push it in sorted_stack
temp < 7
input_stack: [ 9]
sorted_stack: [1, 4, 7]
// pop next element from input_stack and store in temp
temp: 9
// compare temp with top element as it is less so push it in sorted_stack
temp < 9
input_stack: [ ]
sorted_stack: [1, 4, 7, 9]
Complexity Analysis
Time Complexity: O(n²)
Space Complexity: O(n)
Lets code the algorithm now
public class Solution {
public ArrayList<Integer> solve(ArrayList<Integer> A) {
Stack<Integer> input_stack = new Stack<>();
input_stack.addAll(A);
Stack<Integer> sorted_stack = new Stack<>();
while(!input_stack.isEmpty()){
int top = input_stack.pop();
insertInStack(sorted_stack, top);
}
return new ArrayList<>(sorted_stack);
}
private void insertInStack(Stack<Integer> sorted_stack, int temp){
if(sorted_stack.isEmpty() || sorted_stack.peek() >= temp){
sorted_stack.push(temp);
return;
}
int top = sorted_stack.pop();
insertInStack(sorted_stack, temp);
sorted_stack.push(top);
}
}
Output
input_stack : [4, 7, 1, 9]
sorted_stack : [1, 4, 7, 9]
