Implementing a Binary Search Tree (BST) in C++

In this article, we have explained the idea of implementing Binary Search Tree (BST) from scratch in C++ including all basic operations like insertion, deletion and traversal.

Binary Search Tree is similar to a graph but with some special properties, a BST (Binary Search Tree) has a node, left pointer and a right pointer. They allow fast lookup, addition and removal of items, and can be used to implement either dynamic sets of items, or lookup tables that allow finding an item by its key.

Binary Search Tree, is a node-based binary tree data structure which has the following properties:

• The left subtree contains only nodes with data less than the root’s data.
• The right subtree contains only nodes with data greater than the root’s data.
• Duplicate nodes shouldn't exist in the tree.

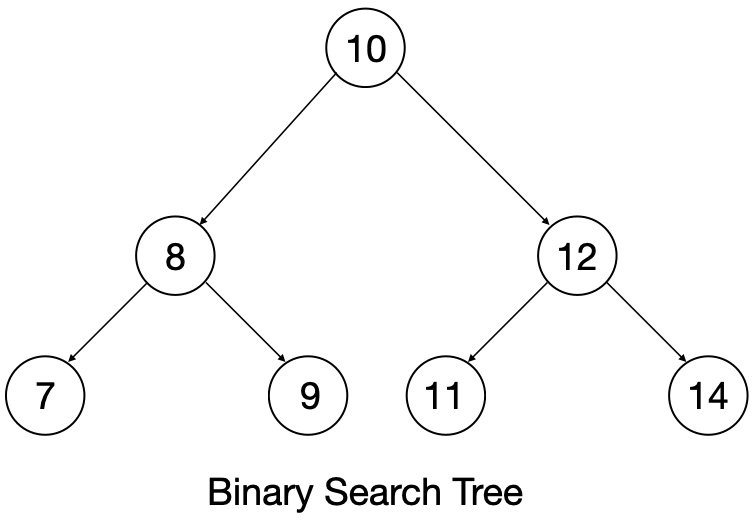
The binary search tree has three operations:

• Searching
• Traversion
• Deletion

For the core functionality of C++ Standard template library, we include <bits/stdc++.h> header file and use std namespace.

#include <bits/stdc++.h>
using namespace std;

We define a binary tree with a Node which contains data and pointers to left and right Node of the tree.

//Creating a Tree Node class
class Node{
public:
    int data;
    Node* left;
    Node* right;
    Node(int d){
        data = d;
        left = NULL;
        right = NULL;
    }
}

Now we'll implement binary search tree functionalities like searching, inserting, travesing and deleting

Searching for a key in binary tree:

We will create a function to search a given key in the binary tree with a starting node.

For searching a particular key we'll first compare the given element with the node->val , if the node->val is more than the key value, we'll search the left subtree from the given node. Similarly, we'll search the right subtree if the node->val is less than the key value.

Implementation:

Node* search(Node* root, int key) {
        if(root == NULL || root->data == key)        
            return root;

        // Key is greater than root's data 
        if(root->data < key) 
            return search(root->right,key);

        // Key is smaller than root's data 
        return search(root->left,key);
     }

Inserting a key in the binary tree:

For insertion of the data in a binary tree we will create a function which returns Node pointer(Node*) and takes in two input parameters: root node and data for insertion.

To insert an element in binary search tree we'll compare the data we want to insert with the tree elements, if the node element's data is less than the data to be inserted, we'll move to the right subtree to find the position to insert. Similarly, if the node->data is more than the data to be inserted we'll move towards left subtree to find the position of insertion of element. If we find the correct position, we create a node with data as data to be inserted and push it into binary tree.

Implementation:

    Node* insert(Node* root, int data) {
        if(root == NULL){
            return new Node(data);
        }
     else{
            Node* cur;
            if(data <= root->data) {
                cur = insert(root->left, data);
                root->left = cur;
            }
            else {
                cur = insert(root->right, data);
                root->right = cur;
            }
        return root;
     }
   }

Visual Representation:

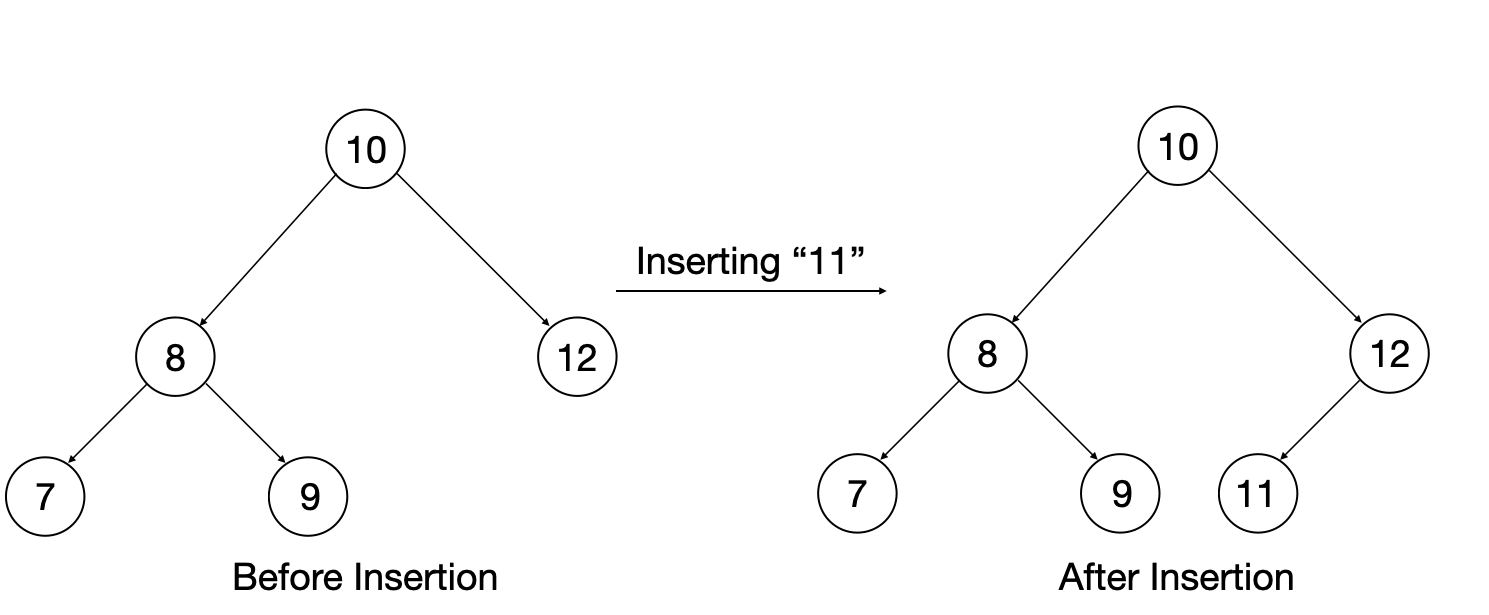
Deleting a key in binary tree:

Deleting a node in binary search tree is similar to insertion, but when we find a node to be deleted, we also delete it's left and right subtree.

In deletion, there are two possibilities to check:

1. If the node to be deleted has children, then the combined system (node+leaves) gets deleted.
2. If the node to be deleted is the leaf, then only the leaf is deleted.

Implementation:

1. If node is leaf then delete the leaf.

    Node* deletenode(Node* root, int k) 
    { 
        // Base case 
        if (root == NULL) 
            return root; 
        //If root->data is greater than k then we delete the root's subtree
        if(root->data > k){ 
            root->left = deletenode(root->left, k); 
            return root; 
        } 
        else if(root->data < k){ 
            root->right = deletenode(root->right, k); 
            return root; 
        } 
  

        // If one of the children is empty 
        if (root->left == NULL) { 
            Node* temp = root->right;
            delete root; 
            return temp; 
        } 
        else if (root->right == NULL) { 
            Node* temp = root->left; 
            delete root; 
            return temp; 
        } 

2. If both children exist then we delete the node(Parent) + the children

else {
          Node* Parent = root;
          // Find successor of the node
          Node *succ = root->right; 
          while (succ->left != NULL) { 
              Parent = succ; 
              succ = succ->left; 
          } 

          if (Parent != root) 
              Parent->left = succ->right; 
          else
              Parent->right = succ->right; 

          // Copy Successor Data  
          root->data = succ->data; 

          // Delete Successor and return root 
          delete succ;          
          return root; 
      } 
  } 

Traversals in binary tree:

There are three types of traversals in binary tree:

• Inorder traversal : In this traversal, we first traverse the left subtree completely, then visit the node and in the end traverse the right subtree.

• Preorder traversal: In this traversal, we first visit the node, then traverse the right subtree completely and then the left subtree.

• Postorder traversal: In this traversal, we first traverse the left subtree then the right subtree and in the end visit the node.

Implementation of the algorithms:

• Inorder traversal:

    void inorder(Node* root){
        if(root == NULL)
            return;
        
        //First recur on left subtree 
        inorder(root->left);
        //Then read the data of child
        cout << root->data << " ";
        // Recur on the right subtree
        inorder(root->right);
    }

• Preorder traversal:

    void preorder(Node* root){
        if(root == NULL)
            return;
        
        //First read the data of child
        cout << root->data << " ";
        //Then recur on left subtree 
        preorder(root->left);
        //Then Recur on the right subtree
        preorder(root->right);
    }

• Postorder traversal:

    void postorder(Node* root){
        if(root == NULL)
            return;
        
        //Then recur on left subtree 
        postorder(root->left);
        //Then Recur on the right subtree
        postorder(root->right);
        //First read the data of child
        cout << root->data << " ";
    }

Complete implementation of binary tree:

We can now implement a binary search tree in C++ using above functions:
Firstly, we'll include the header files which are necessary.

#include <bits/stdc++.h>
using namespace std;

Creating a Tree Node class

class Node{
public:
    int data;
    Node* left;
    Node* right;
    Node(int d){
        data = d;
        left = NULL;
        right = NULL;
    }

Then let's define a function to insert node in the tree.

    
    Node* insert(Node* root, int data) {
        if(root == NULL){
            return new Node(data);
        }
     else{
            Node* cur;
            if(data <= root->data) {
                cur = insert(root->left, data);
                root->left = cur;
            }
            else {
                cur = insert(root->right, data);
                root->right = cur;
            }
        return root;
     }
    }

Also, defining the inorder traversal.

    //Indorder traversal
    void inorder(Node* root){
        if(root == NULL)
            return;
        
        inorder(root->left);
        cout << root->data << " ";
        inorder(root->right);
    }

Implementing the search function.

    //Searching function
    Node* search(Node* root, int key) {
            if(root == NULL || root->data == key)
                return root;

            // Key is greater than root's data
            if(root->data < key)
                return search(root->right,key);

            // Key is smaller than root's data
            return search(root->left,key);
         }

Implementing deletenode function.

    Node* deletenode(Node* root, int k) 
    { 
        // Base case 
        if (root == NULL) 
            return root; 
        //If root->data is greater than k then we delete the root's subtree
        if(root->data > k){ 
            root->left = deletenode(root->left, k); 
            return root; 
        } 
        else if(root->data < k){ 
            root->right = deletenode(root->right, k); 
            return root; 
        } 
  

        // If one of the children is empty 
        if (root->left == NULL) { 
            Node* temp = root->right;
            delete root; 
            return temp; 
        } 
        else if (root->right == NULL) { 
            Node* temp = root->left; 
            delete root; 
            return temp; 
        } 
else {
            Node* Parent = root;
            // Find successor of the node
            Node *succ = root->right; 
            while (succ->left != NULL) { 
                Parent = succ; 
                succ = succ->left; 
            } 

            if (Parent != root) 
                Parent->left = succ->right; 
            else
                Parent->right = succ->right; 

            // Copy Successor Data  
            root->data = succ->data; 

            // Delete Successor and return root 
            delete succ;          
            return root; 
        } 
    } 
};

Here the main() function starts, in which we'll initialize the Tree node with 0 and fill in the data necessary.

int main(){
    Node Tree(0);
    Node* root = NULL;
    //Number of nodes to be inserted
    int t;
    cin>>t;
    while(t--){
        int data;
        cin>>data;
        root = Tree.insert(root,data);
    }

Using levelOrder function defined in the Node class.

    //levelOrder
    Tree.levelOrder(root);

Using search() function to find the required key value in the tree.

    //Searching data
    cout << "Enter the data to find:";
    int data;
    cin>>data;
    Node* find_element = Tree.search(root,data);

Using deletenode funtion to delete a node.

    int delete_data;
    cin>>delete_data;
    Node* deleteelement = Tree.deletenode(root,delete_data);
    return 0;
}

Thank you for reading this article at OpenGenus and enhancing your knowledge!