Open-Source Internship opportunity by OpenGenus for programmers. Apply now.

In this article, we will begin our discussion by briefly explaining about transitive closure and graph powering. We will also see the application of graph powering in determining the transitive closure of a given graph.
What is Transitive Closure of a graph ?
In any Directed Graph, let's consider a node i as a starting point and another node j as ending point. For all (i,j) pairs in a graph, transitive closure matrix is formed by the reachability factor, i.e if j is reachable from i (means there is a path from i to j) then we can put the matrix element as 1 or else if there is no path, then we can put it as 0.
Suppose we are given the following Directed Graph,
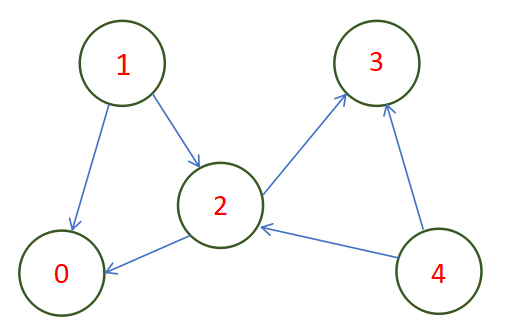
Then, the reachability matrix of the graph can be given by,
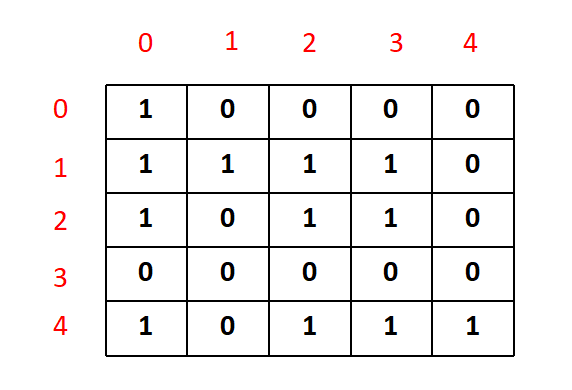
This matrix is known as the transitive closure matrix, where '1' depicts the availibility of a path from i to j, for each (i,j) in the matrix.
What is Graph Powering ?
Graph powering is a technique in discrete mathematics and graph theory where our concern is to get the path beween the nodes of a graph by using the powering principle.
In simple words, if we take the rth power of any given graph G then that will give us another graph G(r) which has exactly the same vertices, but the number of edges will change. In the powered graph G(r) there will be a connection between any two nodes if there exits a path which has a length less than r between them.
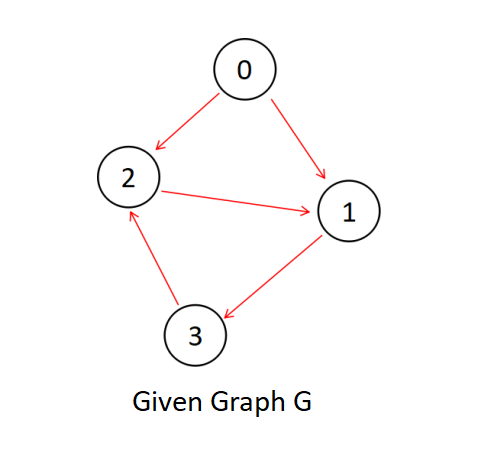
Suppose we have a directed graph as following,
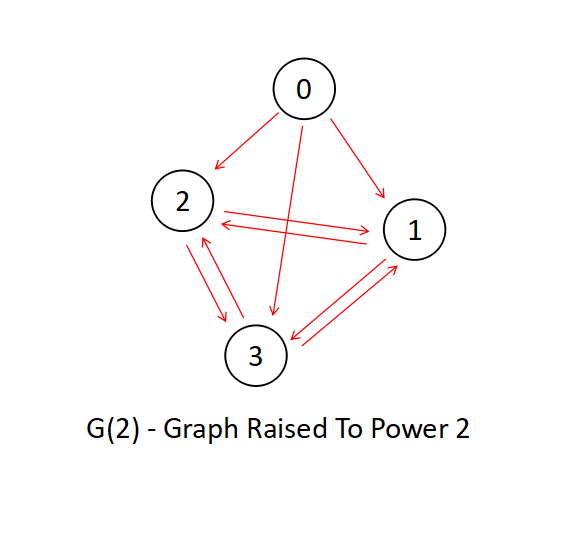
Now let's generate a new graph from the above graph by powering it to r=2, i.e. G(2), Graph powered 2,
As you can see, the existing graph G has been updated with new edges between those nodes, who has a path difference of less than 2 (as r=2) here.
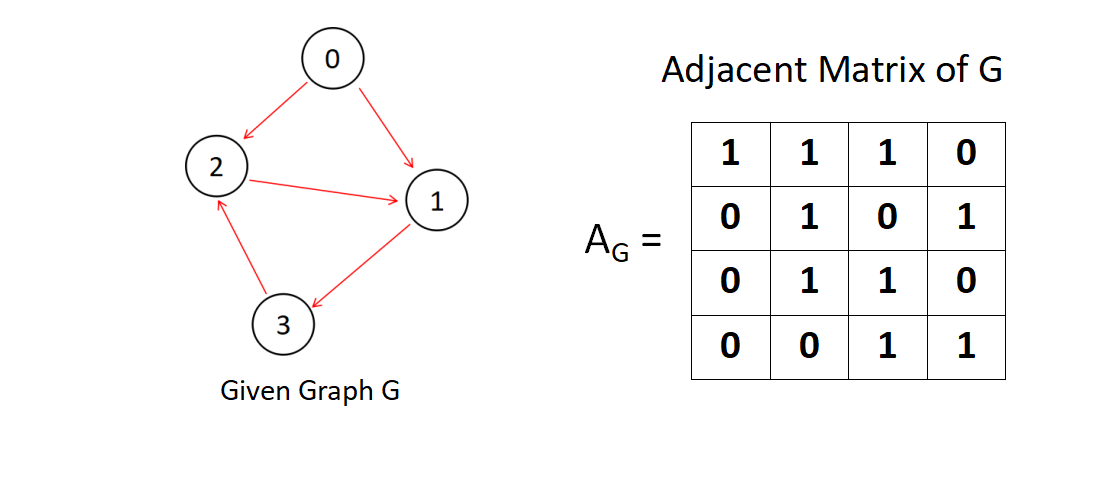
But the question arises on how to implement this in programming ? We can not use direct images for the calculations, but there is a solution to every problem for a programmer, and the solution here is the Adjacent Matrix.
Adjacent matrix is a matrix that denotes 1 for the position of (i,j) if there is a direct edge between ith node and the jth node and denotes 0 otherwise.
Let's perform an experiment for an important conclusion.
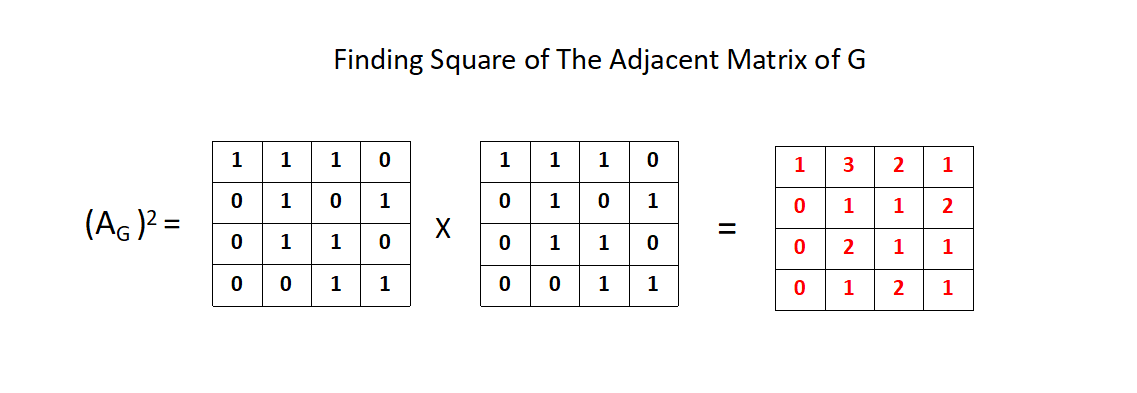
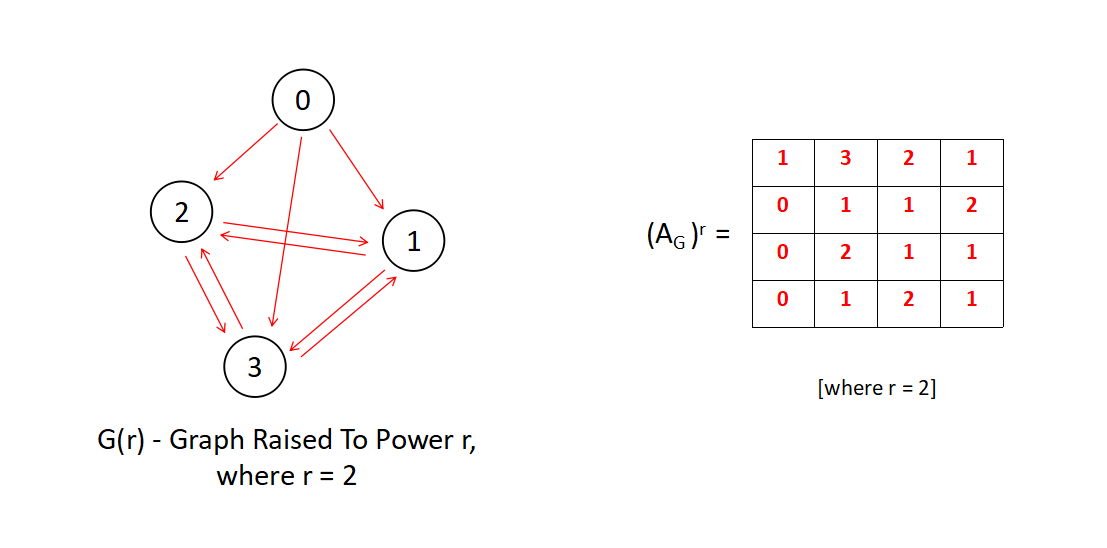
So we have a directed graph and it's adjcent matrix. Let's take the rth power of the Adjacent Matrix, we will get something like below.
For simplicity we have taken r = 2, adjacent matrix raised to the power 2, gives us another matrix as shown above.
What does the matrix(i.e. generated by the square of Adjacent matrix) signify ?
Lets's bring out the G(r=2) graph into picture and observe closely on what the matrix signify,
By a little deep observation, we can say that (i,j) position of the rth powered Adjacent Matrix speaks about the number of paths from i to j in G(r) that has a path length less than equal to r.
For example the value of the (0,1) position is 3. In the G(r=2) graph, we can see there are two paths whose path length are less than equal to 2 from 0 to 1, they are - [0---1,0---2---1 & 0---3---1]
Similarly we can determine for other positions of (i,j).
How to Find Transitive Closure by Graph Powering ?
What will happen if we find G(r=n) for any given graph G, where n is the total number of nodes in G ?
We will get a graph which has edges between all the ith node and the jth node whose path length is equal to n at maximum. For any graph without loops, the length of the longest path will be the number of nodes in it.
So by raising the Adjacent matrix of a given graph G to the power of n, we can get a matrix having some entries (i,j) as 0, which means there are not at all any path between ith node and the jth node which has a maximum path difference of n, where n is the total number of nodes in the graph.
This gives us the main idea of finding transitive closure of a graph, which can be summerized in the three steps below,
- Get the Adjacent Matrix for the graph
- Raise the adjacent matrix to the power n, where n is the total number of nodes.
- Replace all the non-zero values of the matrix by 1 and printing out the Transitive Closure of matrix.
Step 1 - Get The Adjacent Matrix
You will need a two dimensional array for getting the Adjacent Matrix of the given graph. Here are the steps;
- Get the total number of nodes and total number of edges in two variables namely num_nodes and num_edges.
- Create a multidimensional array edges_list having the dimension equal to num_nodes * num_nodes
- Run a loop num_nodes time and take two inputs namely first_node and second_node everytime as two nodes having an edge between them and place the edges_list[first_node][second_node] position equal to 1.
- Finally after the loop executes we have an adjacent matrix available i.e edges_list.
int num_nodes,num_edges;
cin >> num_nodes >> num_edges;
int** edges_list = new int*[num_nodes];
for(int i=0;i<num_nodes;i++)
{
edges_list[i] = new int[num_nodes];
for(int j=0;j<num_nodes;j++)
{
edges_list[i][j] = 0;
}
}
for(int i=0;i<num_edges;i++)
{
int first_node,second_node;
cin >> first_node >> second_node;
edges_list[first_node][second_node] = 1;
if(i<num_nodes)
edges_list[i][i]=1;
}
Time Complexity - O(V^2), space complexity - O(V^2), where V is the number of nodes
Step 2 - Raising The Adjacent Matrix To The Power Of Total Number Of Nodes
This algortihm uses the simplest approach of matrix powering, just like in algebra we multiply two matrices in row-column method.
We will be following some steps to achieve the end result,
- First of all lets create a function named matrix_powering that returns void and takes two parameters namely edges_list i.e. the adjacent matrix and num_nodes i.e. the number of nodes.
- Create two multidimensional array which has the same dimension as that of edges list. One of them will be a blank matrix namely result which will act as an auxilliary matrix for holding values during main calculation. Another one is named matrix, in which the entries of edges_list should be copied.
- Main algortihm will consist of four loops. The outer most loop is to multiply the matrix upto num_nodes times.The second and third loop will act as transitition vertices for the multiplication and the inner most loop is for the intermediate vertices. We will take the row by column multiplication and place the sum in a variable name sum. After the innermost loop terminated the iteration we will place the sum value in out result array.
- Finally we will copy the entries of result to the entries of matrix
Please take a pen and paper and start executing the main algorithm of loops for understanding it better.
void matrix_powering(int** edges_list,int num_nodes)
{
int result[num_nodes][num_nodes];
int** matrix = new int*[num_nodes];
for(int i=0;i<num_nodes;i++)
{
matrix[i] = new int[num_nodes];
for(int j=0;j<num_nodes;j++)
{
matrix[i][j] = edges_list[i][j];
}
}
int sum = 0;
for (int i = 0; i < num_nodes; i++)
{
for ( int c = 0 ; c < num_nodes ; c++ )
{
for (int d = 0 ; d < num_nodes ; d++ )
{
for (int k = 0 ; k < num_nodes ; k++ )
{
sum += matrix[c][k]*matrix[k][d];
}
result[c][d] = sum;
sum = 0;
}
}
for ( int c = 0 ; c < num_nodes ; c++ ) {
for ( int d = 0 ; d < num_nodes ; d++ ) {
matrix[c][d] = result[c][d];
result[c][d] = 0;
}
}
}
transitive_closure(matrix,num_nodes);
}
Time Complexity - O(V^4), space complexity - O(V^2), where V is the number of nodes
Step 3 - Replace All The Non-Zero Values and Printing the Adjacent Matrix
This step is easy, we just need to traverse the entire multi-dimensional array and replace the occurance of non-zero terms with 1. Later we need to print the matrix by calling a function print_transitive_closure.
/// utility function to print the transitive closure matrix
void print_transitive_closure(int** output, int num_nodes)
{
cout << endl;
for(int i=0;i<num_nodes;i++)
{
for(int j=0;j<num_nodes;j++)
{
cout << output[i][j] << " ";
}
cout << endl;
}
}
/// utility function to convert powering matrix to transitive closure matrix
void transitive_closure(int** matrix, int num_nodes)
{
for(int i=0;i<num_nodes;i++)
{
for(int j=0;j<num_nodes;j++)
{
if(matrix[i][j]>0)
{
matrix[i][j] = 1;
}
}
}
print_transitive_closure(matrix,num_nodes);
}
The Entire Code
#include <iostream>
#include <cmath>
#include <cstdlib>
using namespace std;
/// utility function to print the transitive closure matrix
void print_transitive_closure(int** output, int num_nodes)
{
cout << endl;
for(int i=0;i<num_nodes;i++)
{
for(int j=0;j<num_nodes;j++)
{
cout << output[i][j] << " ";
}
cout << endl;
}
}
/// utility function to convert powering matrix to transitive closure matrix
void transitive_closure(int** matrix, int num_nodes)
{
for(int i=0;i<num_nodes;i++)
{
for(int j=0;j<num_nodes;j++)
{
if(matrix[i][j]>0)
{
matrix[i][j] = 1;
}
}
}
print_transitive_closure(matrix,num_nodes);
}
/// utility function to power the matrix
void matrix_powering(int** edges_list,int num_nodes)
{
int result[num_nodes][num_nodes];
int** matrix = new int*[num_nodes];
for(int i=0;i<num_nodes;i++)
{
matrix[i] = new int[num_nodes];
for(int j=0;j<num_nodes;j++)
{
matrix[i][j] = edges_list[i][j];
}
}
int sum = 0;
for (int i = 0; i < num_nodes; i++)
{
for ( int c = 0 ; c < num_nodes ; c++ )
{
for (int d = 0 ; d < num_nodes ; d++ )
{
for (int k = 0 ; k < num_nodes ; k++ )
{
sum += matrix[c][k]*matrix[k][d];
}
result[c][d] = sum;
sum = 0;
}
}
for ( int c = 0 ; c < num_nodes ; c++ ) {
for ( int d = 0 ; d < num_nodes ; d++ ) {
matrix[c][d] = result[c][d];
result[c][d] = 0;
}
}
}
transitive_closure(matrix,num_nodes);
}
int main()
{
int num_nodes,num_edges;
cin >> num_nodes >> num_edges;
int** edges_list = new int*[num_nodes];
for(int i=0;i<num_nodes;i++)
{
edges_list[i] = new int[num_nodes];
for(int j=0;j<num_nodes;j++)
{
edges_list[i][j] = 0;
}
}
for(int i=0;i<num_edges;i++)
{
int first_node,second_node;
cin >> first_node >> second_node;
edges_list[first_node][second_node] = 1;
if(i<num_nodes)
edges_list[i][i]=1;
}
cout << "Input Adjacent Matrix Graph:" << endl;
for(int i=0;i<num_nodes;i++)
{
for(int j=0;j<num_nodes;j++)
{
cout << edges_list[i][j] << " ";
}
cout << endl;
}
matrix_powering(edges_list,num_nodes);
return 0;
}
Complexity Of the Algorithm
As we can see, the main algorithm function matrix_powering has four loops embeded and each one iterates for num_nodes time, hence the time complexity of the algortihm is O(V^4).
Similarly the space complexity of the algorithm is O(V^2) as we are using two multidimensional arrays having dimension num_nodes * num_nodes at maximum.
Improving The Time Complexity
We can improve the time complexity of the above mentioned algorithm by using Euler's Fast Powering Algorithm, that is based on Binary Exponentiation technique for getting a matrix to the nth power.
This algorithm will be operating on O(V^3 * logV) time complexity, where V is the number of vertices.
matrix_powering is the function which has a while loop, where the value of n becomes half with each iteration, which is of O(logV) time complexity,later each conditional statement is calling matrix_multiplication function, which has three loops embeded and of O(V^3). This total algorithm thus gives a rise to the complexity of O(V^3 * logV).
#include <iostream>
#include <cmath>
#include <cstdlib>
using namespace std;
/// utility function to print the transitive closure matrix
void print_transitive_closure(int** output, int num_nodes)
{
cout << endl;
for(int i=0;i<num_nodes;i++)
{
for(int j=0;j<num_nodes;j++)
{
cout << output[i][j] << " ";
}
cout << endl;
}
}
/// utility function to convert powering matrix to transitive closure matrix
void transitive_closure(int** matrix, int num_nodes)
{
for(int i=0;i<num_nodes;i++)
{
for(int j=0;j<num_nodes;j++)
{
if(matrix[i][j]>0)
{
matrix[i][j] = 1;
}
}
}
print_transitive_closure(matrix,num_nodes);
}
/// utility function to get the identity matrix
void identity_matrix(int** a, int SIZE)
{
for (int i = 0; i < SIZE; i++)
for (int j = 0; j < SIZE; j++)
a[i][j] = (i == j);
}
//matrix_multiplication method
void matrix_multiplication(int** a, int** b,int SIZE)
{
int** res = new int*[SIZE];
for(int i=0;i<SIZE;i++)
{
res[i] = new int[SIZE];
for(int j=0;j<SIZE;j++)
{
res[i][j] = 0;
}
}
for (int i = 0; i < SIZE; i++)
for (int j = 0; j < SIZE; j++)
for (int k = 0; k < SIZE; k++)
{
res[i][j] += a[i][k] * b[k][j];
}
for (int i = 0; i < SIZE; i++)
for (int j = 0; j < SIZE; j++)
a[i][j] = res[i][j];
}
// matrix powering to nth power
void matrix_powering(int** a, int n, int** res,int num_nodes)
{
identity_matrix(res,num_nodes);
while (n > 0) {
if (n % 2 == 0)
{
matrix_multiplication(a, a,num_nodes);
n /= 2;
}
else {
matrix_multiplication(res, a,num_nodes);
n--;
}
}
transitive_closure(res,num_nodes);
}
int main()
{
int num_nodes,num_edges;
cin >> num_nodes >> num_edges;
int** edges_list = new int*[num_nodes];
for(int i=0;i<num_nodes;i++)
{
edges_list[i] = new int[num_nodes];
for(int j=0;j<num_nodes;j++)
{
edges_list[i][j] = 0;
}
}
for(int i=0;i<num_edges;i++)
{
int first_node,second_node;
cin >> first_node >> second_node;
edges_list[first_node][second_node] = 1;
if(i<num_nodes)
edges_list[i][i]=1;
}
cout << "Input Adjacent Matrix Graph:" << endl;
for(int i=0;i<num_nodes;i++)
{
for(int j=0;j<num_nodes;j++)
{
cout << edges_list[i][j] << " ";
}
cout << endl;
}
int** result = new int*[num_nodes];
for(int i=0;i<num_nodes;i++)
{
result[i] = new int[num_nodes];
for(int j=0;j<num_nodes;j++)
{
result[i][j] = 0;
}
}
matrix_powering(edges_list,num_nodes,result,num_nodes);
}