
Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
Given a string of integers, find the count of sub-strings of given string which are divisible by 6. This problem can be solved using Dynamic Programming in O(N) time complexity where N is the length of the string.
For example 1.
Input: "68412" Output: 6
Explanation: Since 6, 84, 12, 684, 8412, 68412 are the only substrings which are divisible by 6.
Example 2.
Input: "350648" Output: 6
Explanation : 0, 6, 48, 648, 5064, 35064 are the only substrings which are divisble by 6.
We are assuming here that if substring contains more than one digit then its most significant digit can never be 0, thats why in above example substring '0' is counted whereas substrings '0648' and '06' are not counted in the result since they are mathematically equal to substrings '648' and '6' respectively, which we are already counted in result.
Approach1 : Brute Force Method
In this method we will traverse string and will check every substring possible that if it is divisible by 6 or not.Condition for integer to be divisible by 6 is: It must be divisible by 2 and sum of its digits must be divisible by 3.
For applying the sum check, we will keep track of variable rem in which we will store modulus by 3 of sum of all previous digits. Everytime we encounter a new digit while traversing we will update the value of rem. To keep track of count we take a variable named count, every time we get substring divisible by 6 we increase the value of count by 1.
Example1:
For Input string : 68412
First of all we will convert string into character array. We will run nested loop from index i=0 to i= (length of string)-1 and j=i to j=(length of string)-1.
For above example,
for i=0, initially count=0, rem=0,
when i=0, j=0 => x=6, count=0, rem=0,
x%2=0 and (x+rem)%3=0 => 6 is a substring which is divisble by 6.
=> count =1 (we incremented count by 1).
rem = 0 ( since rem = (x+rem)%3)
when i=0, j=1 => x=8, count=1, rem=0,
x%2 =0 (x+rem)%3 !=0 => 68 is a substring which is not divisible by 6.
=> count=1 (count is not incremented).
rem = 2 ( since rem = (x+rem)%3)
when i=0, j=2 => x=4, count=1, rem=2,
x%2=0 (x+rem)%3=0 =>684 is a substring which is divisible by 6.
=> count=2 (we incremented count by 1).
rem = 0 ( since rem = (x+rem)%3)
when i=0 j=3 => x=1, count=2, rem=0
x%2 != (x+rem)%3 !=0 => 6841 is a substring which is not divisible by 6.
=> count=2 (count is not incremented).
rem = 1 ( since rem = (x+rem)%3)
when i=0 j=4 => x=2, count=2, rem=1
x%2=0 (x+rem)%3=0 =>68412 is a substring which is divisible by 6.
=> count=3 (we incremented count by 1).
rem =0 ( since rem = (x+rem)%3)
now for i=1, we make the value of rem 0 again i.e rem
when i=1, j=1 => x=8, count =3, rem =0
x%2 =0 (x+rem)%3 !=0 => 8 is a substring which is not divisible by 6.
=> count=3 (count is not incremented).
rem =2 ( since rem = (x+rem)%3)
when i=1, j=2 => x=4, count=3, rem=2
x%2=0 (x+rem)%3=0 => 84 is a substring which is divisible by 6.
=>count=4 (we incremented count by 1).
rem = 0 ( since rem = (x+rem)%3)
when i=1, j=3 => x=1, count =4, rem = 0
x%2 =0 (x+rem)%3 !=0 => 841 is a substring which is not divisible by 6.
=> count=4 (count is not incremented).
rem = 1 ( since rem = (x+rem)%3)
when i=1, j=4 => x=2, count=4, rem =1
x%2=0 (x+rem)%3=0 => 8412 is a substring which is divisible by 6.
=> count=5 (we incremented count by 1).
rem = 0 ( since rem = (x+rem)%3)
now for i=2, we make the value of rem 0 again i.e rem =0.
when i=2, j=2 => x=4, count=5, rem =0
x%2=0 (x+rem)%3 !=0 => 4 is a substring which is not divisible by 6.
=> count=5 (count is not incremented).
rem = 1 ( since rem = (x+rem)%3)
when i=2, j=3 => x=1, count=5, rem =1
x%2 !=0 (x+rem)%3 !=0 => 41 is a substring which is not divisible by 6.
=> count=5 (count is not incremented).
rem =2 ( since rem = (x+rem)%3)
when i=2 j=4 => x=2, count=5, rem =2
x%2 =0 (x+rem)%3 !=0 => 412 is a substring which is not divisible by 6.
=> count=5 (count is not incremented).
rem =1 ( since rem = (x+rem)%3)
now for i=3, we make the value of rem 0 again i.e sum =0.
when i=3 j=3 => x=1, count=5, rem =0
x%2 !=0 (x+rem)%3 !=0 => 412 is a substring which is not divisible by 6.
=> count=5 (count is not incremented).
rem =1 ( since rem = (x+rem)%3)
when i=3 j=4 => x=2, count=5, rem =1
x%2 =0 (x+rem)%3 =0 => 12 is a substring which divisible by 6.
=> count=6 (count is incremented by 1).
rem =0 ( since rem = (x+rem)%3)
now for i=4, we make the value of rem 0 again i.e rem =0.
when i=4 j=4 => x=2, count=6, rem = 0
x%2 =0 (x+rem)%3 !=0 => 2 is a substring which is not divisible by 6.
=> count=6 (count is not incremented).
rem = 2 ( since rem = (x+rem)%3)
And hence finally we got count=6 in output.
Now we will see it by code
import java.util.*;
public class solve{
public static int CountSubStrings(char[] str)
{
int count = 0;
int rem = 0;
int x = 0;
for(int i = 0; i < str.length; i++)
{
rem = 0;
for(int j = i; j < str.length; j++)
{
x = str[j] - '0';
if(i == j && x == 0 )
{
count++;
break;
}
if(x % 2 == 0 && (rem + x) % 3 == 0)
{
count++;
}
rem = (rem + x) % 3;
}
}
return count;
}
public static void main(String []args){
Scanner sc = new Scanner(System.in);
String s = sc.nextLine();
char[] str = s.toCharArray();
int result = CountSubStrings(str);
System.out.println(result);
}
}
Input: 68412
Output: 6
Input: 1608576
Output: 7
Input: 350648
output: 6
Time Complexity : O(n^2)
Complexity of above brute force approach is O(n^2).
If we observe this method properly we can see that we have to calculate some values more than once sometimes (depending on the value of string).
For example in above input 68412:
When i=0 and j=1, rem=0 (as previous substring is 6 and 6%3==0, so for remaining substring 8412, the number of substring divisible by 6 is independent of previous substring.
when i=1 and j=0, we have to again calculate number of substring divisible by 6 for substring 8412, which we have previously calculated.
So to avoid calculating the same value repeatedly and optimize above approach, we can use "Dynamic Programming" approach to store these values and avoid recalculation and so improve the run time complexity.
Approach 2: Dynamic Programming Method
- Since we want to avoid recalculation of values for an index i and rem which is being already calculated, so will take a 2D matrix where one dimension i.e i will keep track of x (digit at index i) and second i.e j will keep track of rem and now for every possible combination of x and rem we can store value in matrix.
dp[i][j] represent number of substring started from index i with reminder j.
Since we want all the substring starting from index 0 to index n-1 and which gives remainder 0 when divided by 6, our final answer will be :
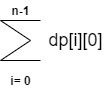
- Let x is the i'th digit in string and for every x, value of rem possible are 0,1,2 (as we are taking % 3) so size of matrix will be (n x 3) (here n is length of input string).
Outer loop will run from i=0 to i=n and inner loop will run from j=0 to j=2.
Lets first see it with code than with example.
import java.util.*;
public class Solve{
static int result = 0;
public static int helper(int i, int rem, char[] str, int[][] dp)
{
if(i == str.length)
return 0;
if(dp[i][rem] != -1)
return dp[i][rem];
int x = str[i] - '0';
if(x % 2 == 0 && (x + rem) % 3 == 0)
{
result = 1 + helper(i + 1, (x + rem) % 3, str, dp);
}
else
{
result = helper(i + 1, (x + rem) % 3, str, dp);
}
dp[i][rem] = result;
return dp[i][rem];
}
public static int countSubStrings(char[] str)
{
int n = str.length;
int count = 0;
// for storing the values
int[][] dp = new int[n][3];
for(int i = 0; i < n; i++)
{
for (int j = 0; j < 3; j++)
{
dp[i][j] = -1; // initialize all values to -1
}
}
for(int i = 0; i < str.length; i++)
{
if(str[i] - '0' == 0)
{
count++;
}
else
{
count = count + helper(i, 0, str, dp);
}
}
return count;
}
public static void main(String []args){
Scanner sc = new Scanner(System.in);
String s = sc.nextLine();
char[] str = s.toCharArray();
int ans = countSubStrings(str);
System.out.println(ans);
}
}
Lets understand this code with the example below.
Suppose the input string s is "684"
-
First it is converted in character array str[] = 684.
-
Now we pass this char array to Method countSubStrings().
-
Since our string is of length 3, so value of n = 3.
-
We initialize a variable count with 0, this variable will keep track of count of substrings divisible by 6.
-
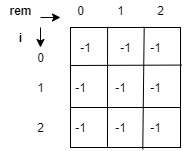
There are 3 possible values for any number for remainder when divided by 3, so we take a 2 D matrix i.e of size nx3 (here n is length of input string) .
-
We initialize all the entries of this matrix with -1 initially. It will later help us to decide whether if the value we want to calculate is already calculated or not.
-
Now we will traverse the string.
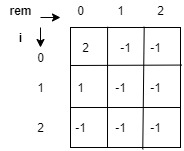
for i=0, helper(0 , 0, str, dp) function is called (since count = 0 + helper(0, 0, str, dp). After this call the dp matrix will look like this:
-
for i=1, the value of dp[i][0] is already calculated, so we don't need to calculate this value again and we can just reuse this value.
The final dp matrix will look like this:
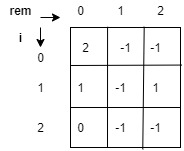
now our final answer will be count and,
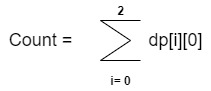
=> count = dp[0][0]+dp[1][0]+dp[2][0]
=> count = 3 is our answer for string 684.
and if we cross check our answer and see since 6, 684, 84 are the substrings which are divisible by 6. hence our approach is correct.
Since we are traversing a string once and only with a single loop,
Time Complexity :O(n)
