Find articulation point in Graph

In this article we'll be discussing on how to find articulation point in Graph. Firstly we'll discuss on the Introduction to Articulation Points. Secondly, we'll understand the Articulation Points concept with a graph example. At the end will write a Pseudo code & implementation for the same.

Following are the sections of this article:-

1. Introduction
2. Example for Articulation Points
3. Pseudo Code and Implementation
4. Time and Space Complexity
5. Conclusion

1. Introduction

Consider a Graph(G) which is formed by Vertices(V) and Edges(E) is said to have an Articulation point of Cut vertex(V) if by removing it and all the edges(E) associated with it results in increase of the total number of connected components in the Graph(G).
In other words, A vertex in an Undirected graph is an Articulation point if and only if by removing it, it disconnects the graph.

2. Example for Articulation Points

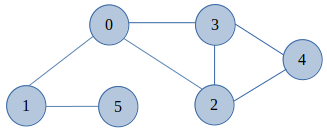
Example, Let us consider the below Fig a

Fig a - Undirected Graph

From the above Graph diagram, vertex 0 and all the edges associated with it, i.e. the edges 0-1, 0-2 and 0-3 are removed. If we want to reach the vertex 2, 3 or 4 from the vertices 1 and 5, their will be no path left and hence the graph will split into two separate components. Similarly if the vertex 1 is removed, then it'll disconnect the vertex 5 for all the other vertices.
These steps are shown in the below diagram Fig b(1 & 2),

(1)
(2)

Fig b(1 & 2) - After removal of Articulation Points(0 & 1) from Fig a

From the above Graph example its clear that, removal of an articulation point will increase the number of connected graph and hence for the Graph(G) at Fig a articulation points are vertex 0 & 1.

3. Pseudo Code and Implementation

As our main focus to produce this article is to write an algorithm to find Articulation points in a Graph, Lets get started.
Consider a Graph(G) that is formed by vertices V and edges E, Following are the ideal steps-

1. Remove a vertex v from the Graph(G).
2. Check, If the Graph(G) is still remains as a connected graph, we say no articulation points. This can be processed by DFS traversal algorithm.
   Else, we print those vertex v as an articulation point or Cut vertex in the given Graph(G).

• Pseudo Code
  Following is the Pseudo code snippets function, for finding all articulation points in a graph.

function totalArticulation_points(adj[][], V)
    count = 0
    for i = 0 to V
        visited[i] = false
    initial_val = 0 
    for i = 0 to V
        if visited[i] == false
            DFS(adj, V, visited, i)
            initial_val = initial_val+1

    for i=0 to V
        for j = 0 to V
            visited[j] = false
            copy[j] = adj[i][j]
            adj[i][j]=adj[j][i]=0

        nval = 0
        for j= 0 to V
            if visited[j] == false AND j != i
                nval = nval + 1
                DFS(adj, n, visited, j)
        if nval > initial_val
            count = count + 1
        for j= 0 to V
            adj[i][j] = adj[j][i] = copy[j]
    return count

From the above code snippet, we'll get count of all the Articulation points from the Graph. We also see a Traversal approach(DFS) has been used.
Similar to our previous discussion on Bridges, even Articulation points can be found using DFS. Kindly go through the basics of the concept of DFS from this article An algorithm to find all bridges in a Graph.

• Implementation
  We have implemented the code in Python(3.8)

from collections import defaultdict
  
#Using adjacency list representation, This class represents an undirected graph

class Graph:
  
    def __init__(self,vertices):
        self.V= vertices #No. of vertices
        self.graph = defaultdict(list) # default dictionary to store graph
        self.Time = 0
  
    # function to add an edge to graph
    def addingEdge(self,u,v):
        self.graph[u].append(v)
        self.graph[v].append(u)
  
    '''A recursive function that finds and prints Cut Vertex
       or articulation points using DFS traversal
    
    u --> The vertex to be visited next
    visited[] --> A list, which keeps tract of visited vertices
    disc[] --> A list, which Stores discovery times of visited vertices
    parent[] --> A list, which Stores parent vertices in DFS tree
    cv[] --> A list, which Stores the Cut Vertex or articulation points 
    '''
    def cutVertexDetails(self,u, visited, parent, low, disc, cv):
 
        #Count of children in current node 
        children = 0
 
        # Marking the current node as visited and print it
        visited[u]= True
 
        # Initialize discovery time and low value
        disc[u] = self.Time
        low[u] = self.Time
        self.Time += 1
 
        #Recursive execution for all the vertices adjacent to this vertex
        for v in self.graph[u]:
            if visited[v] == False :
                parent[v] = u
                children += 1
                self.cutVertexDetails(v, visited, parent, low, disc, cv)

                low[u] = min(low[u], low[v])
  
                # u is a Cut Vertex in following cases 
                # if,u is root of DFS tree & has two or more chilren. 
                if parent[u] == -1 and children > 1: 
                    cv[u] = True
                # If, u is not root & low value of one of its child 
                # is more than discovery value of vertex u. 
                if parent[u] != -1 and low[v] >= disc[u]: 
                    cv[u] = True  
                          
            elif v != parent[u]: 
                # Update low value of u for parent function calls.
                low[u] = min(low[u], disc[v])
  
    # DFS based function to find all Cut Vertex or articulation point.
    # It uses recursive function, inside function findCutVertex()
    def findCutVertex(self):
  
     # Mark all the vertices as not visited and Initialize parent and visited
        visited = [False] * (self.V)
        disc = [float("Inf")] * (self.V)
        low = [float("Inf")] * (self.V)
        parent = [-1] * (self.V)
        #To store Cut vertex or articulation points
        cv = [False] * (self.V) 
        
        # to find Cut vertex or articulation points 
        # in DFS tree rooted with vertex 'i'
        for i in range(self.V):
            if visited[i] == False:
                self.cutVertexDetails(i, visited, parent, low, disc, cv)
        for p, value in enumerate (cv):
            if value == True:
                print(p)
  
# Program Execution starts from here
if __name__ == '__main__':  

    # Creating a graph given in the above diagram (Fig a)
    g = Graph(6)
    g.addingEdge(0, 1)
    g.addingEdge(0, 3)
    g.addingEdge(0, 2)
    g.addingEdge(1, 5)
    g.addingEdge(2, 3)
    g.addingEdge(2, 4)
    g.addingEdge(3, 4)
    print("\nArticulation points in graph are:")
    g.findCutVertex()

# Output @console after running the script
#
# Articulation points in graph are:
# 0
# 1

4. Time and Space Complexity

The Time complexity of the above approach is O(V + E) where V is the total number of Vertices and E is the total number of Edges in the Graph(G). And coming to Space complexity of the above approach is O(V) where V is the total number of Vertices in the Graph(G).

5. Conclusion

Lastly we are at the end of the article. We explored a bit on the Articulation Points concept of graph. This article is the continuation of my previous article, An algorithm to find all bridges in a Graph. There are many applications in which we make use of this Articulation Points and Bridges. Few are-

• Finding a vulnerable node in a topology of network.
• Calculating the Shortest path or Feasible path between source and destination.

Hope it was an informative article, Thanks!