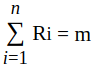Maximum cut problem

In this article we'll be discussing on the concept of Maximum cut problem. Firstly will understand its basic concept with Introduction. Secondly, with a graph example will deep-dive into the concept. Later we'll discuss an interesting way of finding solution with Algorithm. Lastly we'll conclude the article with application of the same.

Following are the sections of this article:-

1. Introduction
2. Example for Maximum Cut
3. Complexity Class
4. Algorithm
5. Conclusion

1. Introduction

Let us discuss what exactly is a Cut and understand the concept of it. Later we connect the dots to the end for our article Maximum Cut problem.

A Cut is a partition of the vertices of a graph in to two separate or disjoint subsets. At the end we get a set called cut-set which consists of the set of edges that have one endpoint in each subset of the partition.
Formally, A Cut C = (S,T) is a partition of V of a graph G = (V,E) into two subsets S and T, Where u belongs to S and v belongs to T or (u,v) belongs to `E'.

The Maximum cut, as the name suggests, we want the cut that maximizes the number of crossing edges in an Undirected Graph(G).
In other words, A cut is maximum if the size of the cut is not smaller than the size of any other cut or it atleast cut's all the crossing edge in a Graph.

2. Example for Maximum Cut

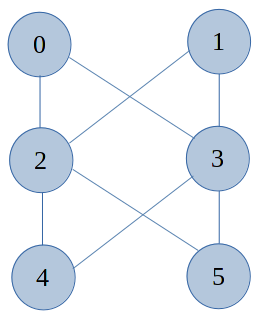
Let us consider an Undirected Graph(G) as example Fig a,

Fig a - Undirected Graph(G)

From the above graph(G), there are totally 6 vertices and 8 edges in the given Undirected Graph. Following is the Max Cut diagram Fig b for the same.

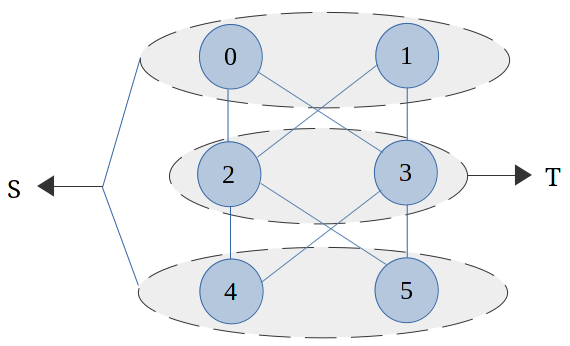
Fig b - Max Cut for Fig a

From the Fig b, Maximum Cut for the graph in Fig a is 8. Only 8 edges and there is indeed a cut in which every single one of those edges crosses it. Also, the vertices 2 and 3 belongs to set T, and the vertices 0, 1, 4 and 5 take the set S. There are no edges internal to T, there are no edges internal to S. Every edge has one endpoint in each.

3. Complexity Class

Let us first discuss about computational complexity. Later we'll describe to which mainly Complexity Class this Maximum Cut problem belongs to. In computational complexity theory, a complexity class is a set of computational problems of related resource-based complexity. The two most commonly analyzed resources are time and space or memory.

This Maximum Cut Problem, in generally, is computationally intractable and it'll belong to ==NP-complete problem==. More precisely, the decision version of the question where we're given a graph we want to know whether or not there exists a cut that cuts atleast a certain number of edges, that's an NP-complete problem(for which no polynomial time algorithm is known). Like most NP-complete problems, there are some computational tractable special cases. From our example (Fig a) the case of bipartite graphs. One definition of a bipartite graph is a graph in which there exists a cut, so that every single edge is crossing it.

4. Algorithm

As per my understanding their are lot of research and theories are in process to find a particular or a perfect algorithm for this problem.
We'll discuss one such approach to find the solution with an algorithm, which we have taken as a reference from the lecture notes of Carnegie Mellon University(from the notes, Section 2.1.2).

• Greedy Algorithm to find Maximum-Cut
  Considering a Undirected Graph(G) formed by Vertices(V) & Edges(E). We start ordering on the Vertices(V) as V1,V2,...Vn and also we have two empty bins or sets S, T (Where these will be having the vertices set once after cut is maximized). Pick the first vertex V1 and place it in S. For each subsequent vertex we place it in the bin or set such that |E(S,T)| is maximized.

As we are trying to maximize the cut, we initially define a Theorem and later we Prove the same with possible assumptions for the above Undirected Graph(G).

Statement of Theorem:
The greedy algorithm is a two-approximation algorithm for MAX-Cut.

Proof:
Consider any edge in the Graph(G). One vertex must come first in the ordering. Call the later vertex as responsible for forming the edge. Let Ri be the number of edges that Vi is responsible for. Since every edge has exactly one responsible vertex. So mathematically we can formulate as follows,

when Vi is added, at least (Ri/2) edges are added to the cut. Reason behind, each of the other vertices adjacent to the Ri edges that Vi is responsible for have already been assigned or placed to set or bins S or T. The set which contains most endpoint vertices of these Ri edges must contain at least (Ri/2) endpoint vertices. By Greedy algorithm, Vi will be added to the other set and thus adding at least (Ri/2) edges to the cut.

Number of edges in final cut

Hence, the algorithm is a two-approximation.

5. Conclusion

At last we are at the end of the article. We have discussed a bit on the below concepts - Cut, Max-Cut, Example on the Maximum cut, Complexity Class. Also we have taken a reference from the lecture notes of Carnegie Mellon University , which helped us in understanding the concept and to find the solution for Maximum Cut with a Greedy Algorithm.
Maximum Cut problem has many application in Industries as well as in Education or Research sector. The major application we can think of is VLSI design.

Thanks! Hope it was an informative article.