Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
In this article we'll be discussing on the algorithm to find all bridges in a Graph. Firstly we'll discuss on the Introduction to Bridges. Secondly, we'll understand the bridge concept with a graph example. At the end will write an algorithm & implementation for the same.
Following are the sections of this article:-
Introduction
Example for Bridges
Algorithm
Conclusion
1. Introduction
Consider a Graph(G) which is formed by Vertices(V) and Edges(E), an edge in a Graph(G) between vertices(i.e, u and v, which are the subset of V) is called a Bridge or Cut Egde. After removing it their will be no path between u and v.
In other words, An edge in an Undirected Graph is a Bridge if and only if by removing that edge it disconnects the Graph(G). When an edge is removed the Graph(G) becomes a disconnected graph. And if we continued to remove edges, which increases number of disconnected components. A Graph which doesn't contain any bridge is referred as a Bridgeless Graph.
2. Example for Bridges
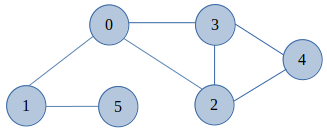
Example, Let us consider the below Fig a
Fig a - Undirected Graph
From the above Graph diagram, If an edge 1-0 is removed then there will be no path left to reach from 1 to 0 vertex. Similarly if edge 1-5 is removed, there'll be no path left that connects vertex 1 and 5. These steps are shown in the below diagram Fig b(1 & 2),
(1)
(2)
Fig b(1 & 2) - After removal of Bridges(1-0 and 1-5) from Fig a
Now that the vertex 1 and 5 are disconnected from the main graph. And there are no edges or path through which we can connect them back to the main graph. Hence, in this case the edges from Fig a 1-0 and 1-5 are the Bridges in the Graph.
3. Algorithm
As our main focus to produce this article is to write an algorithm to all the bridges in a Graph, Lets get started.
To find all the bridges in a given Graph(G) formed by Vertices(V) and Edges(E), also u,v are the subset of V that can be an Edge(E) more precisely a Bridge. Following are the ideal or general steps- For every Edge u,v,
a) Remove the Edge
u,vfrom the Graph(G).
b) Check for graph's connectivity i.e, If the Graph(G) still remainsconnectedby traversing to the adjacent node or vertex if any.
Step (b) can be checked by making use of Depth First Search (DFS) algorithm and at the end, Add u,v back to the Graph(G).
So let us discuss a bit about Depth First Search (DFS) algorithm. As its a major idea behind this article to find all bridges in a Graph(G).
- Depth First Search (
DFS)
It is an algorithm for traversing or searching graph or tree data structures that usesbacktracking. This algorithm explores all the vertices by going forward if any vertex are present in the graph or uses backtracking to reach its starting or previous vertices. DFS can be implemented byStackData structure.
Typical approach or steps for DFS algorithm are -
1. Start by picking a
vertexornodeand push all its adjacentvertexinto a stack.
2. Now, Pop a node from the stack and push all its adjacentvertexinto a stack.
3. Repeat these process until we reach our goal or the stack reaches to its initial state i.e, empty or underflow.
Now we'll focus on, how this Depth First Search algorithm approach can help us to find all bridges in the Graph(G).
In Depth First Search, an edge u,v is a bridge if there does not exist any other path to reach vertex u or an ancestor of u from its subtree rooted with v node or vertex. (where u is parent of v in DFS graph)
Following are the recursive steps, by putting all the previously discussed points in order to find bridge in a Graph(G), These steps are recursively executed until all the Vertices(
V) are visited or traversed.
1. Initially all Vertices(V) of Graph(G) are set to 'False'(implies as not visited). Now we start by traversing to a particular vertex
uand its value is set to 'True'(implies as visited).
2. Also its respective details like discovery time and low value are updated with the current time(for each iteration this time is incremented by 1).
3. At this stage to check for connectivity, we recursively find the all the verticesvadjacent tou.
4. If vertexvis not visited, we update the parent value for vertexvas vertexuand Goto Step 1.
4a. Also check if the subtree rooted withvhas a connection to one of the ancestors ofu, find the minimum low value like - low[u] = min(low[u],low[v]).
4b. Check if the lowest vertex reachable from subtree undervis underuin DFS, then the edgeu-vis a bridge.
5. If vertexvis visited and it is not the current parent, we need to update the low value ofuvertex, low[u] = min(low[u], disc[v]).
- Pseudo Code
Following is the Pseudo code for the above algorithm,
function bridgeDetails(start, visited, disc, low, parent). Here this function accepts the parameters-
Thestartvertex, thevisitedarray to mark when a node is visited, thediscwill hold the discovery time of the vertex, andlowwill hold information about subtrees. Theparentwill hold the parent of the current vertex.
Begin
//the value of 'time' will not be initialized for next function calls mark start as visited
time := 0
set disc[start] := time+1 and low[start] := time + 1
time := time + 1
for all vertex v in the graph G, do
if there is an edge between (start, v), then
if v is visited, then
parent[v] := start
bridgeDetails(v, visited, disc, low, parent)
low[start] := minimum of low[start] and low[v]
if low[v] > disc[start], then
display bridges from start to v
else if v is not the parent of start, then
low[start] := minimum of low[start] and disc[v]
done
End
- Implementation
For the above algorithm, We have implemented the code in Python(3.8)
from collections import defaultdict
#Using adjacency list representation, This class represents an undirected graph
class Graph:
def __init__(self,vertices):
self.V= vertices #No. of vertices
self.graph = defaultdict(list) # default dictionary to store graph
self.Time = 0
# function to add an edge to graph
def addingEdge(self,u,v):
self.graph[u].append(v)
self.graph[v].append(u)
'''A recursive function that finds and prints bridges
using DFS traversal
u --> The vertex to be visited next
visited[] --> A list, which keeps tract of visited vertices
disc[] --> A list, which Stores discovery times of visited vertices
parent[] --> A list, which Stores parent vertices in DFS tree'''
def bridgeDetails(self,u, visited, parent, low, disc):
#Count of children in current node
children = 0
# Mark the current node as visited and print it
visited[u]= True
# Initialize discovery time and low value
disc[u] = self.Time
low[u] = self.Time
self.Time += 1
#Recursive execution for all the vertices adjacent to this vertex
for v in self.graph[u]:
if visited[v] == False :
parent[v] = u
children += 1
self.bridgeDetails(v, visited, parent, low, disc)
low[u] = min(low[u], low[v])
''' If the lowest vertex reachable from subtree
under v is below u in DFS tree, then u-v is
a bridge'''
if low[v] > disc[u]:
print ("%d--%d" %(u,v))
elif v != parent[u]:
# Update low value of u for parent function calls.
low[u] = min(low[u], disc[v])
# DFS based function to find all bridges. It uses recursive
# function bridgeDetails()
def findAllBridge(self):
# Mark all the vertices as not visited and Initialize parent and visited
visited = [False] * (self.V)
disc = [float("Inf")] * (self.V)
low = [float("Inf")] * (self.V)
parent = [-1] * (self.V)
# to find bridges in DFS tree rooted with vertex 'i'
for i in range(self.V):
if visited[i] == False:
self.bridgeDetails(i, visited, parent, low, disc)
# Program Execution starts from here
if __name__ == '__main__':
# Creating a graph given in the above diagram (Fig a)
g = Graph(6)
g.addingEdge(0, 1)
g.addingEdge(0, 3)
g.addingEdge(0, 2)
g.addingEdge(1, 5)
g.addingEdge(2, 3)
g.addingEdge(2, 4)
g.addingEdge(3, 4)
print("\nBridges in the graph are:")
g.findAllBridge()
# Output @console after running the script
#
# Bridges in the graph are:
# 1--5
# 0--1
The time complexity of the above algorithm is O(V + E) where V is the total number of Vertices and E is the total number of Edges in the Graph(G).
4. Conclusion
Lastly we are at the end of the article. We explored a bit on the Bridge concept of graph. And also we have written an algorithm for the same with the help of DFS algorithm. Their is another concept similar to this called Articulation point or Cut vertex. Which mainly focuses on the vertex participation in a graph.
Hope it was an informative article, Thanks!