
Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
In this article, we will learn more about Prim's algorithm and analyze its complexity for different cases and implementation approaches.
Table of contents
- Prim's algorithm
- Complexity analysis
* Time complexity
* Different cases of time complexity
* Space complexity
Prim's algorithm
Prim's algorithm is one of the greedy algorithms that is used to find the minimum spanning tree of a given graph.
Firstly, let us understand more about minimum spanning tree. A Minimum Spanning tree (MST) is a subset of an undirected graph whose connected edges are weighted. The minimum spanning tree connects all the vertices of the graph together with as minimum edge weight as possible. It is void of loops and parallel edges. In the image given below, the subset of graph denoted in red is the minimum spanning tree.
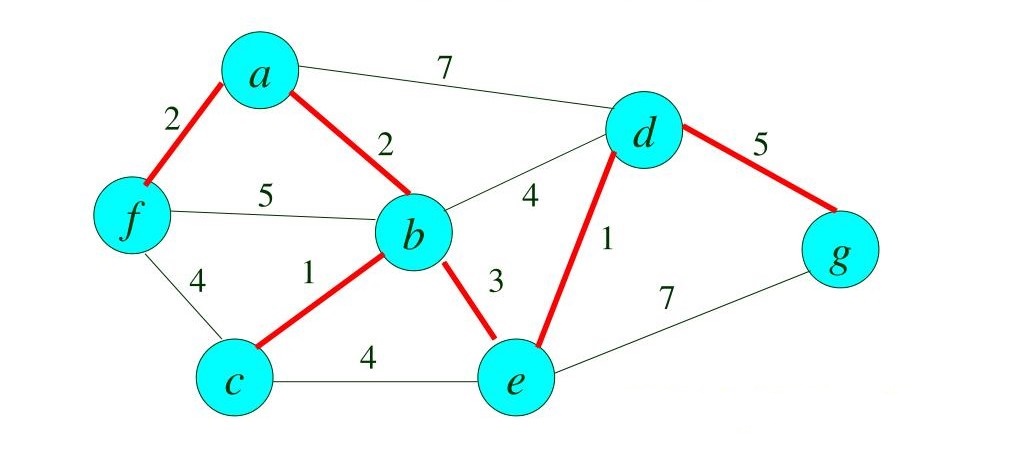
As for Prim's algorithm, starting at an arbitrary vertex, the algorithm builds the MST one vertex at a time where each vertex takes the shortest path from the root node. The steps involved are:
- Pick any vertex of the given network.
- Choose the shortest weighted edge from this vertex.
- Choose the nearest vertex that is not included in the solution.
- If the next nearest vertex has two edges with same weight, pick any one.
- Repeat steps 1-4 till all the vertices are visited, forming a minimum spanning tree.
Let us now move on to the example. Let the given be the graph G.
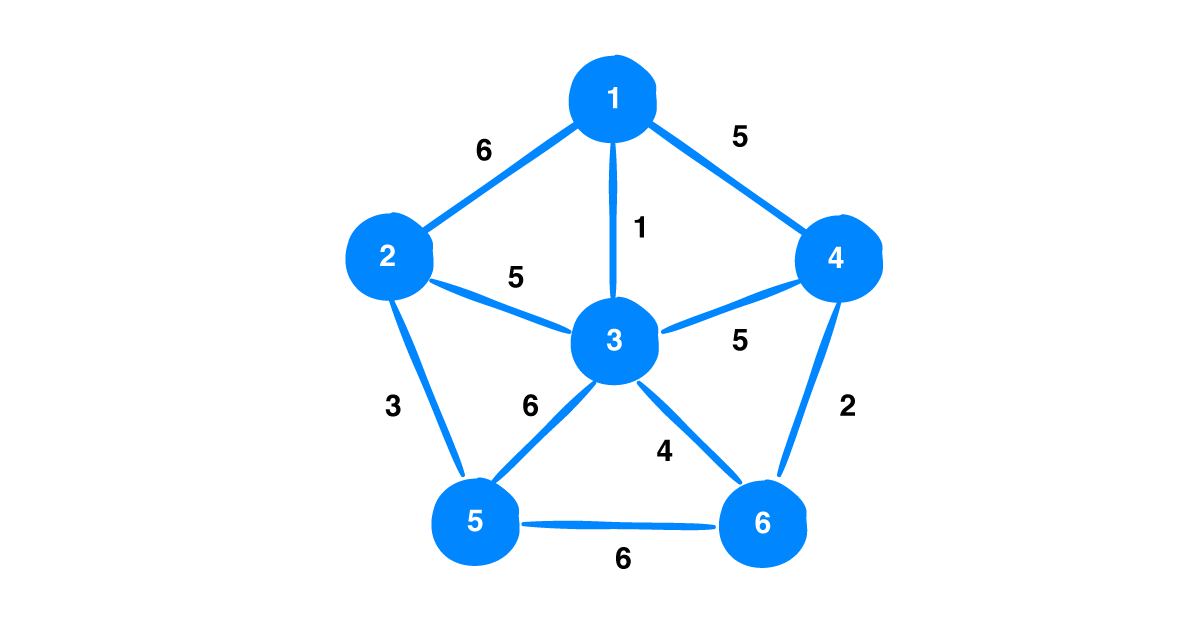
Now, let us choose the vertex 2 to be our first vertex. The weights of the edges from this vertex are [6, 5, 3]. This being a greedy algorithm, it chooses the edge with weight 3 which connects to vertex 5.
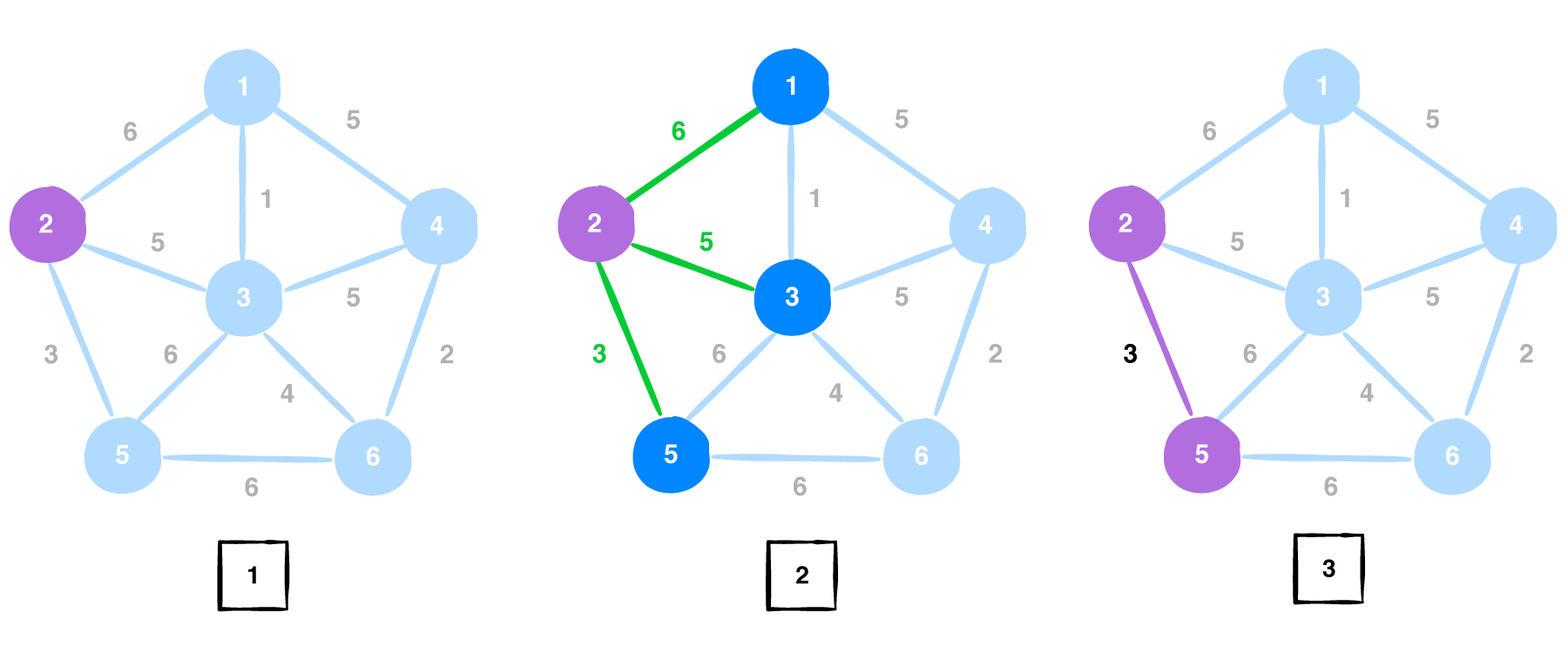
The visited vertices are {2, 5}. We move on to the next vertex in our visited list and now the edge list is [6, 5, 6, 6]. And edge with weight 5 is choosen. The edge between vertices 3 and 5 is removed since bothe the vertices are already a part of the solution.
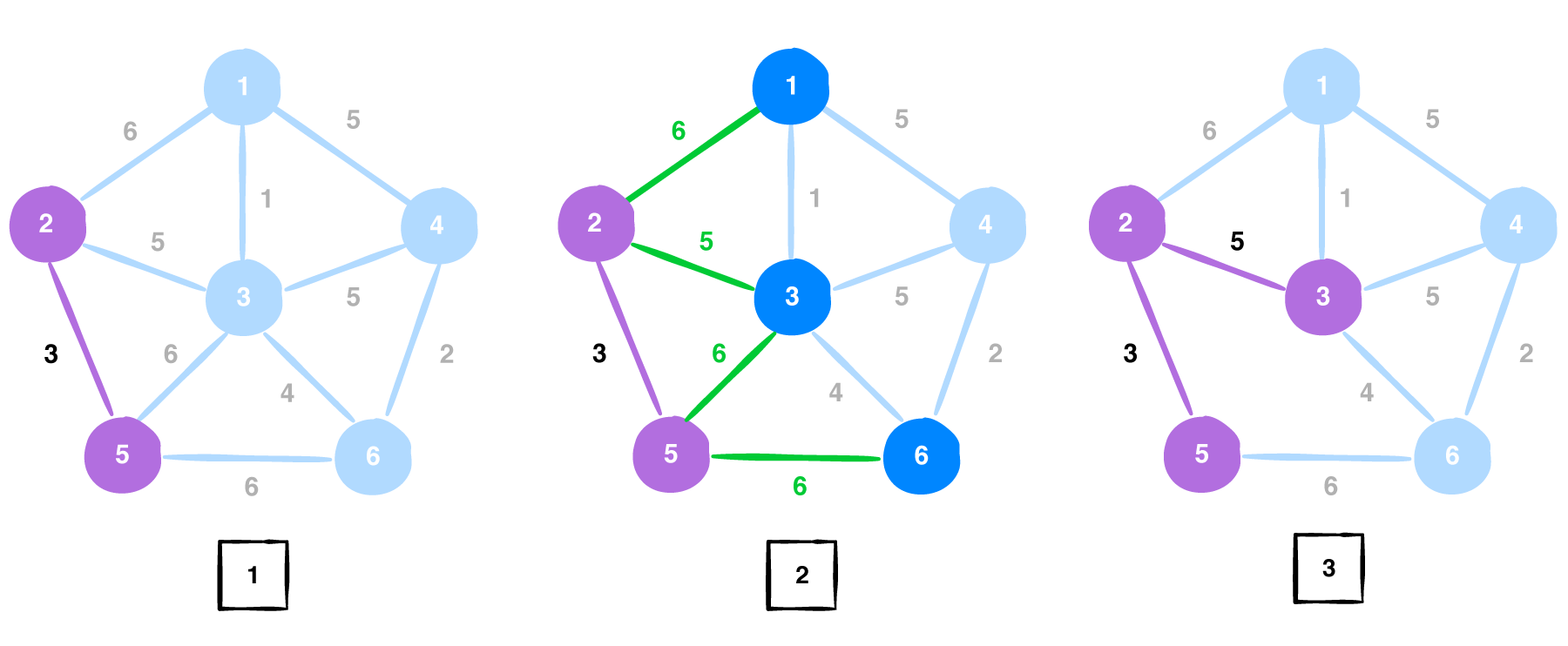
Now, the visited vertices are {2, 5, 3} and the edge list becomes [6, 1, 5, 4, 6]. We choose the edge with weight 1 which is connected to vertex 1.
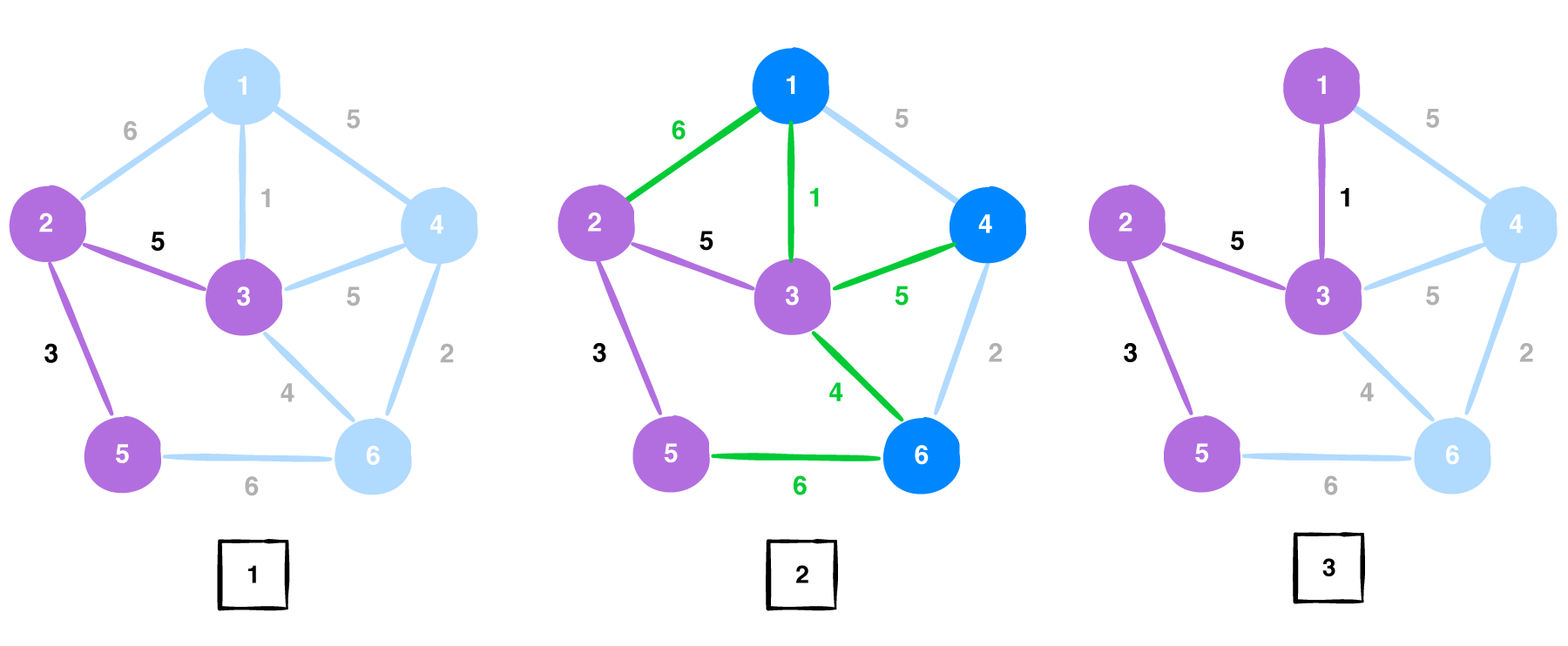
Vertex 1 gets added into the visited vertices {2, 5, 3, 1}. The edge list now becomes [5, 5, 4, 6] and the edge with weight 4 is choosen. The edge between vertices 5 and 6 is removed since bothe the vertices are already a part of the solution.
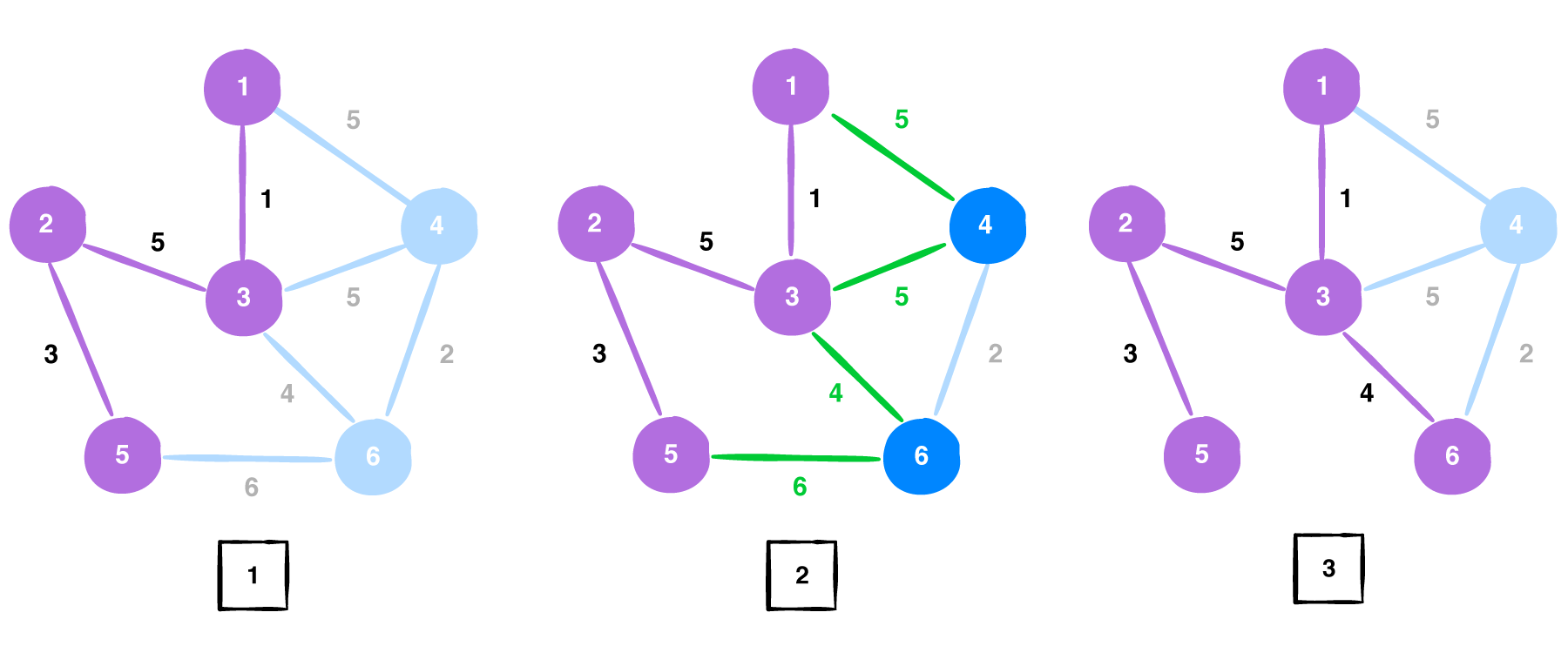
Now the visited vertices are {2, 5, 3, 1, 6} and the edge list is [5, 5, 2]. We choose the edge with weight 4. the edges between vertices 1,4 and vertices 3,4 are removed since those vertices are present in out MST. The Minimum spanning tree that we obtained by using Prim's algorithm for the above given graph G is:
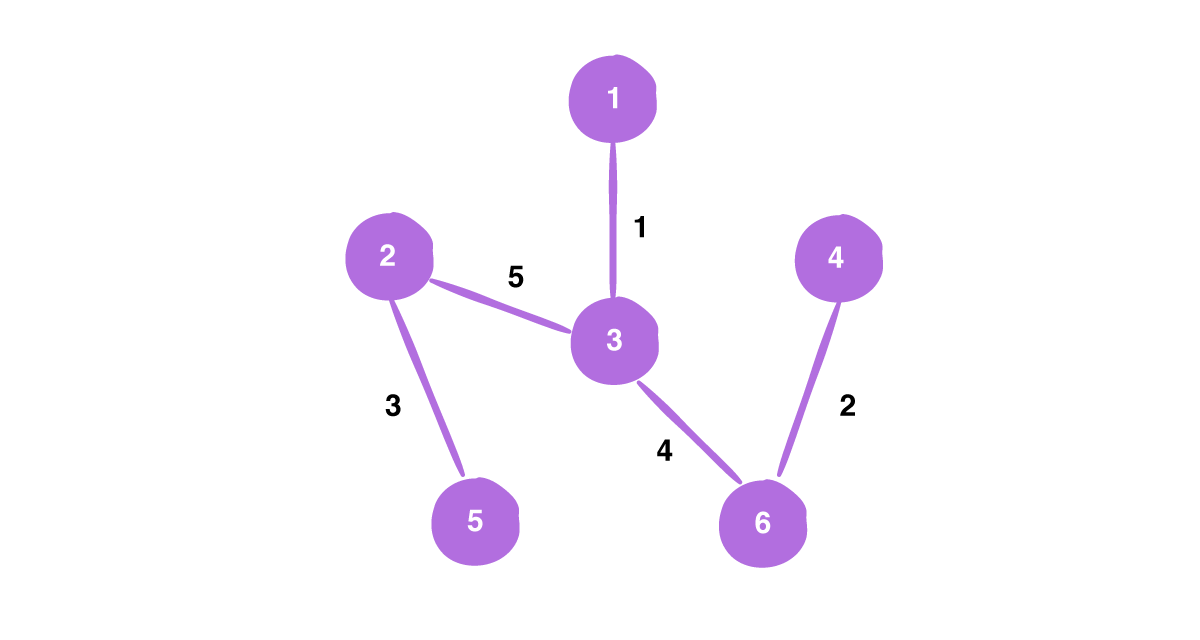
Complexity analysis
Complexity analysis of an algorithm is the part where we find the amount of storage, time and other resources needed to execute the algorithm. These help in the better understanding of the algorithm and aids in finding ways to execute it efficiently.
Time complexity
Time complexity is where we compute the time needed to execute the algorithm.
Using Min heap
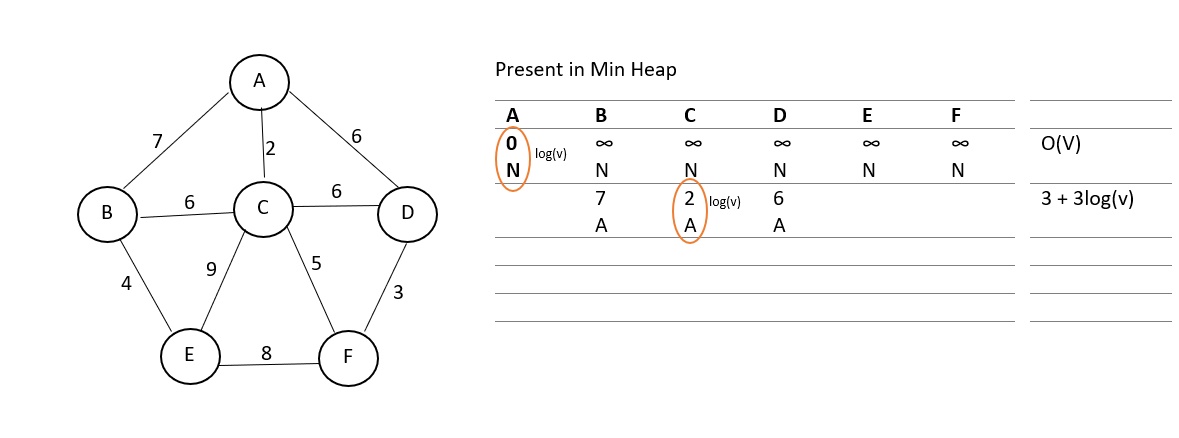
First initialize the key values of the root (we take vertex A here) as (0,N) and key values of other vertices as (∞, N). Initially, our problem looks as follows:
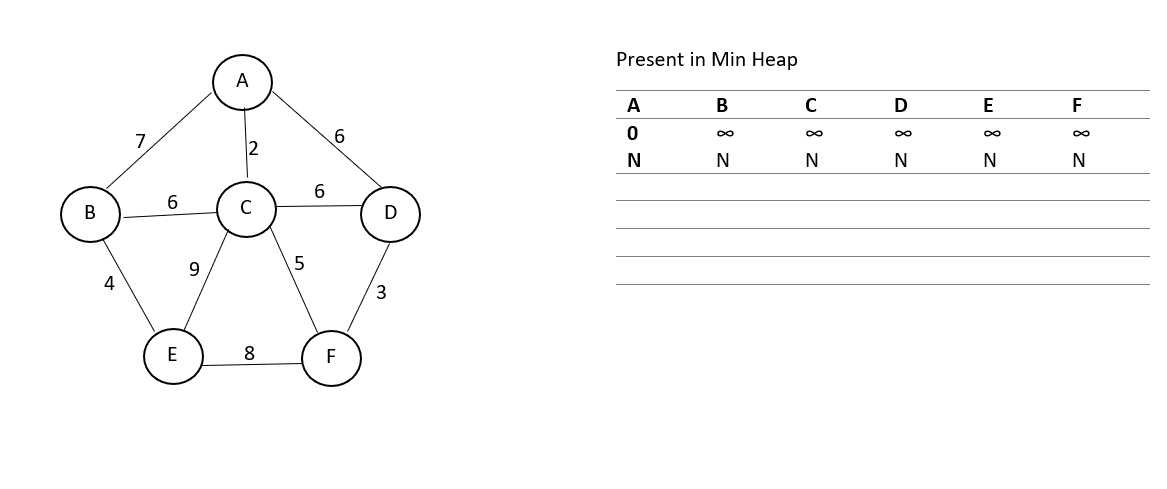
This initialization takes time O(V). Now, we find the neighbours of this vertex, which are 3 in number and we need to perform decrease key operation on these which takes time log(V). Then we delete the root node which takes time log(v) and choose the minimum weighted edge. The updated table looks as follows:
The above procedure is repeated till all vertices are visited. Finally, our problem will look like:
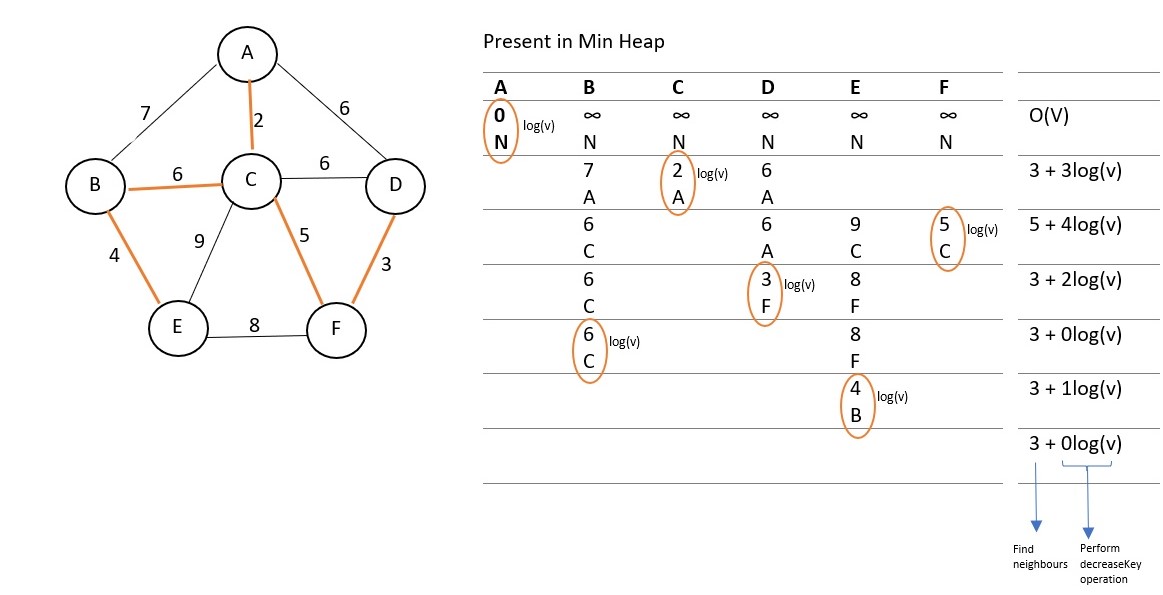
The path traced in orange is the minimum spanning tree.
We find that the sum of time taken to find the neighbeours is twice the sum of edges in the graph and the sum of time taken to perform decreaseKey operation is E(log(V)); where E is the number of edges. Since we performed the delete operation V times, total time taken by it becomes V(log(V)). Adding all these along with time V taken to initialize, we get the total time complexity.
Since E(log(V)) and V(log(V)) dominate over the other terms, we only consider these. So we get our time complexity as:

Hence if we use Min heap, we get the time complexity of Prim's algorithm to be O( V(log(v)) + E(log(V)) ).
- If we consider the above method, both the average case and the worst case time complexities are the same as stated above. Which is, O( V(log(v)) + E(log(V)) ). The best case time complexity for decreaseKey operation is O(1) which makes the best case complexity as O( E(log(V)) ).
Whereas, if we use an adjacency matrix along with Min heap, the algorithm executes more efficiently and has a time complexity of O( E(log(V)) ) in that case as finding the neighbours becomes even more easier with the adjacency matrix.
Using fibonacci heap
Fibonacci Heaps is a more sophisticated implementation of heaps. They have some advantages, which greatly reduce their amortised operation cost. In fact all operations where deletion of an element is not involved, they run in O(1) amortised algorithm. However, due to the complicated nature of Fibonacci Heaps, various overheads in maintaining the structure are involved which increase the constant term in the order.
The operations, which will be implemented, are Insertion, Union, ReturnMin, DeleteMin, DecreaseKey.
No attempt to link the trees in any fashion is made during insertion, melding. We simply add the node or tree in the doubly linked list. Thus, these operations result on O (1) time. However, during delete all the trees are combined in such a manner such that for a particular outdegree of the root, only one tree is present. This reduces the number of trees and by further analysis it can be shown that number of trees which result is of O(log n).
- Using amortised analysis, the running time of DeleteMin comes out be O(log n).
- Using amortised analysis, the running time of DecreaseKey operation comes out to be O(1).
- The Union function runs in a constant time.
In this method, the best, worst and average case time complexity of Prim's algorithm is O(E + logV).
Different cases of time complexity
While analysing the time complexity of an algorithm, we come across three different cases: Best case, worst case and average case.
Best case time complexity
It is the fastest time taken to complete the execution of the algorithm by choosing the optimal inputs. In the best case execution, we obtain the results in minimal number of steps.
For example, let us consider the implementation of Prims algorithm using adjacency matrix. The situation for the best case is, when, only the elements in first row or first column are available for usage and other rows or columns are marked as 0. In this scenario, the complexity for this algorithm will be O(v). Where v is the total number of vertices in the given graph.
Worst case time complexity
It is the slowest possible time taken to completely execute the algorithm and uses pessimal inputs. In the worst case analysis, we calculate upper bound on running time of an algorithm. We must know the case that causes maximum number of operations to be executed.
Let us consider the same example here too. The situation for the worst case is, when all the elements in matrix A is considered for searching and marking suitable edges. In this situation the complexity will be O(v2).
-
Average case time complexity
In average case analysis, we take all possible inputs and calculate computing time for all of the inputs. We then sum all the calculated values and divide the sum by total number of inputs. We must know or predict distribution of cases.
Space complexity
Space complexity denotes the memory space with respect to input size used up by the algorithm until it is executed fully.
To execute Prim's algorithm, we need an array to maintain the min heap. It takes up space E, where E is the number of edges present. We also need an array to store the vertices visited. It takes up space V , where V is the total number of vertices present in the graph.In the example dexcribed above, these represent the set vertices visited and the edge list. Adding both these will give us the total space complexity of this algorithm. Hence Prim's algorithm has a space complexity of O( E + V ).
