Open-Source Internship opportunity by OpenGenus for programmers. Apply now.

In this article, we will discuss about time and space complexities of Tower of Hanoi problem for different cases like worst case, best case and average case.

The topics covered in this article as following:

Problem.
Analysis & Function.
Time Complexity.
Space Complexity.
Conclusion

Problem

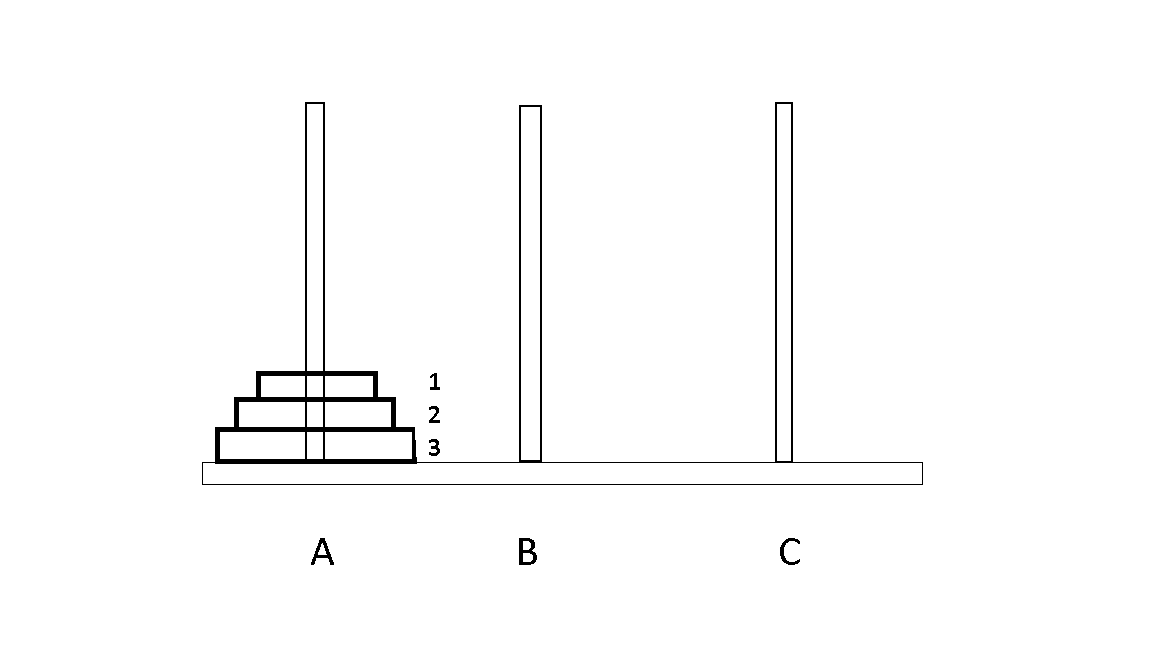
There are 3 Rods A, B and C. Some disks of different sizes are given which can slide onto any Rod . Initially all of those are in A rod in order of size with largest disk at the bottom and smallest disk at the top. We have to move all the disks from A rod to C rod. At the end ,C rod will have disks in the same order of size . there are some rules :

only one disk can be moved from one peg to another peg at a time.
A disk can be placed only on top of a larger one .
A disk can be moved from top only.

Analysis & Function

Let's look at some cases based on no. of disks:

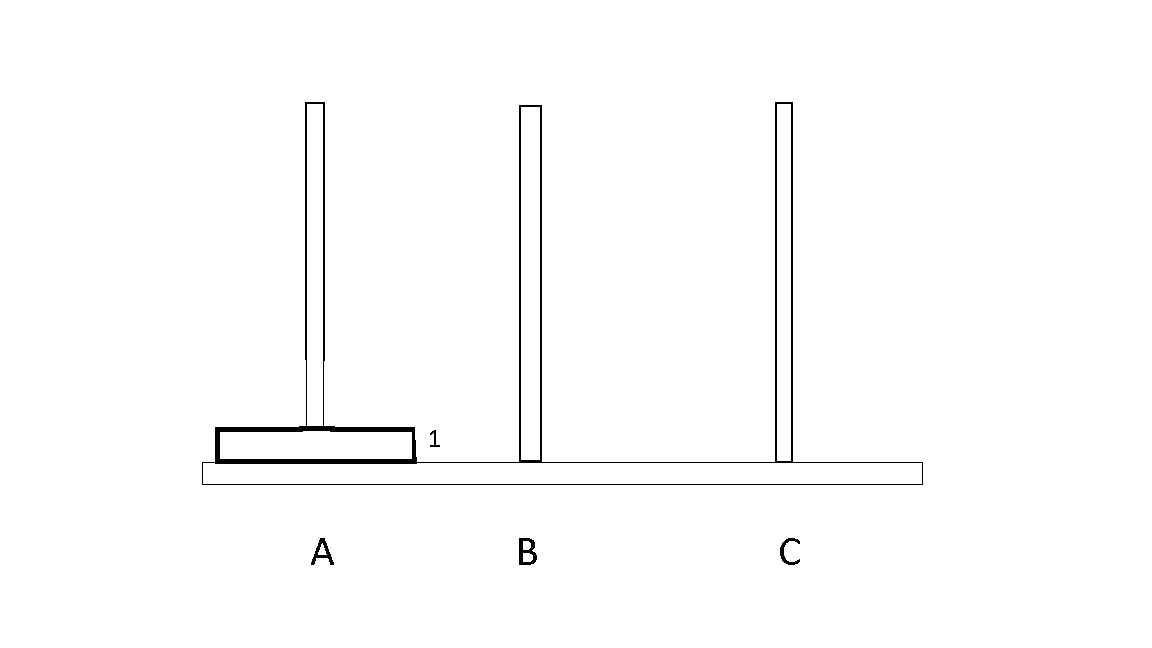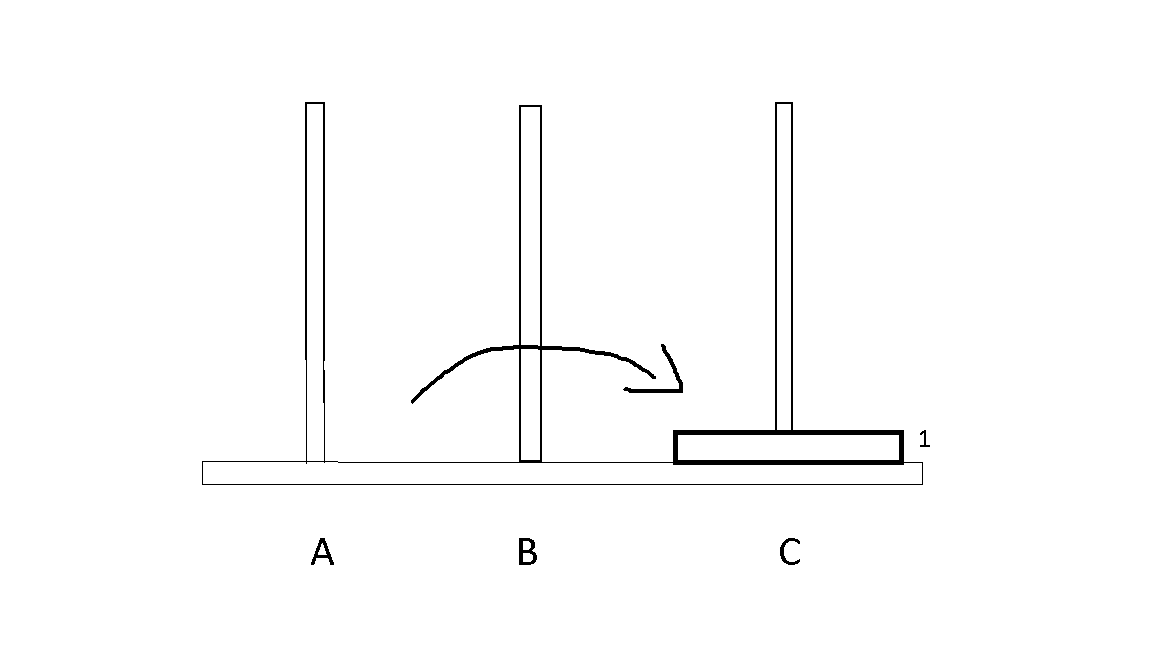
1. One disk

Suppose, we have one disk which has to move from A to C.
We can just move it in one step like the following,

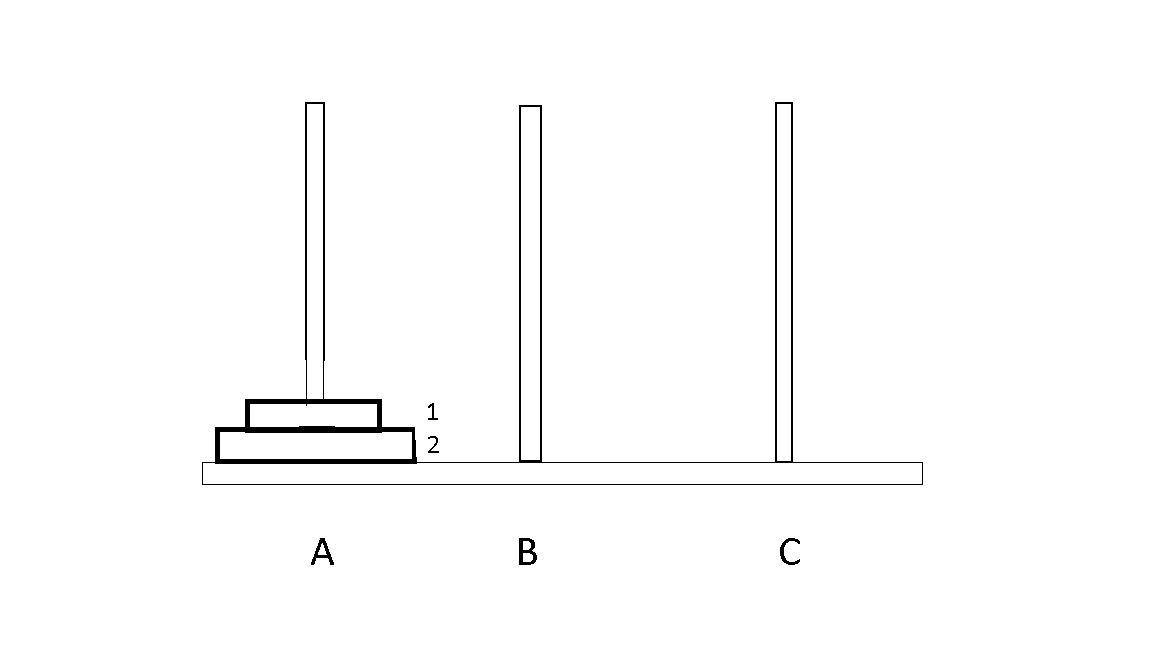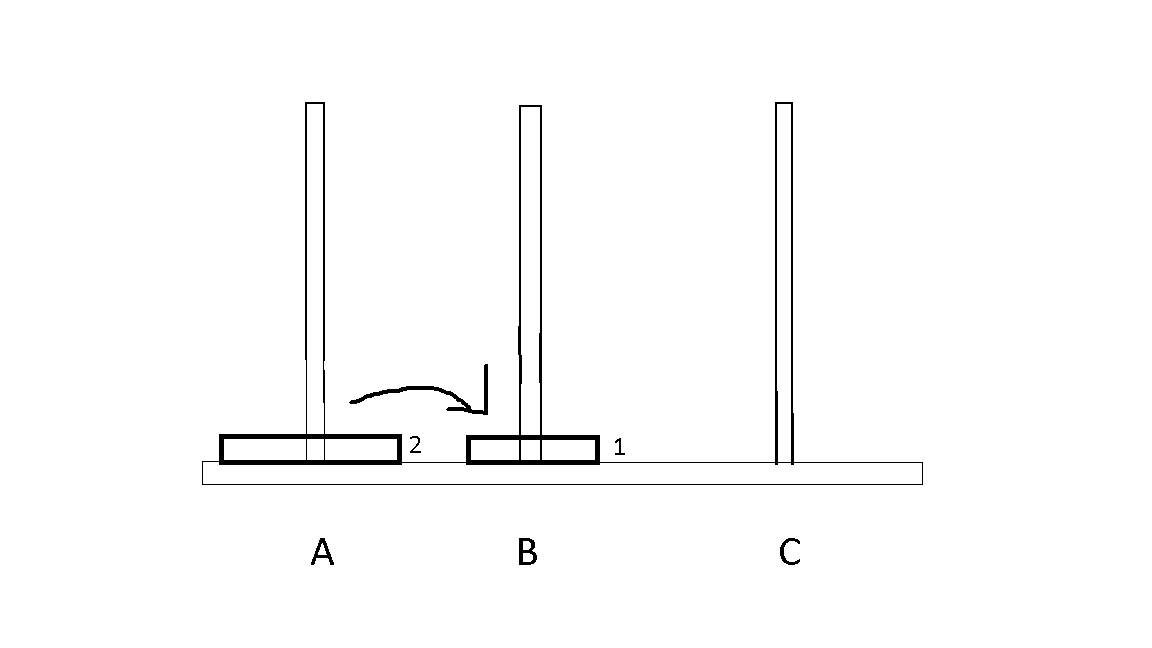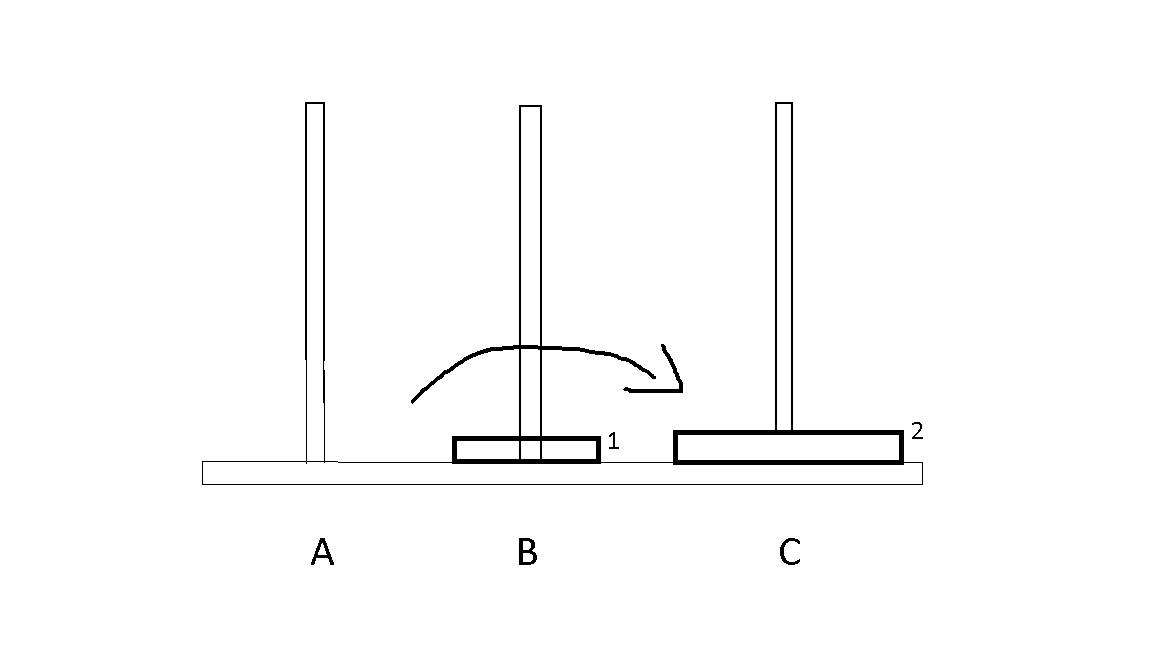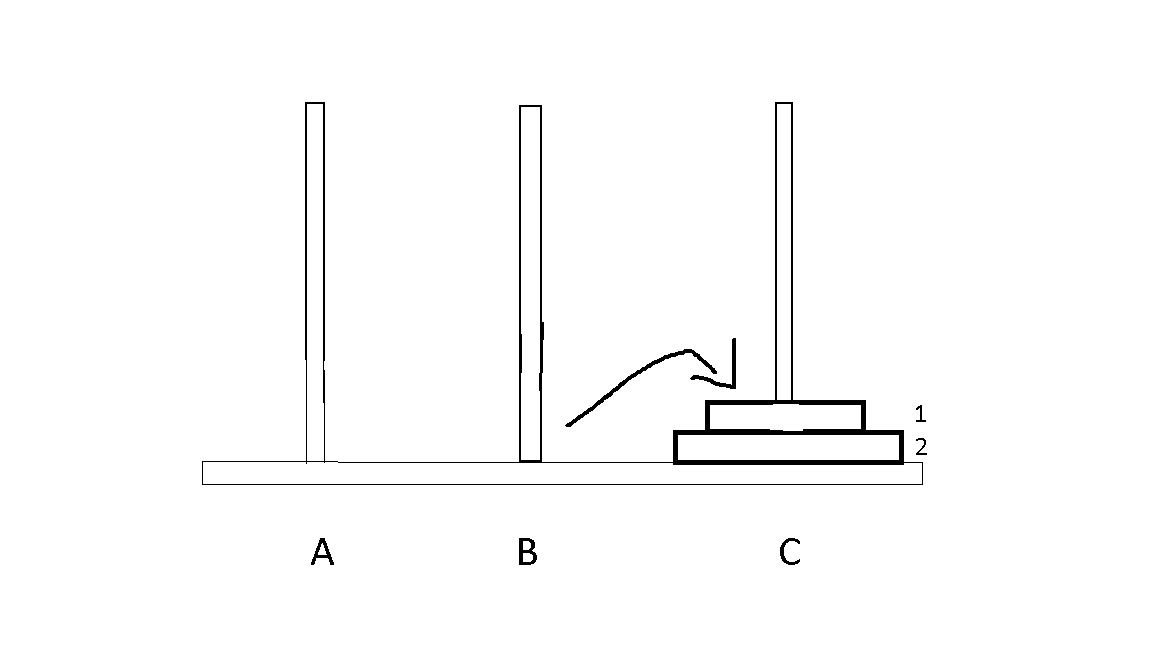
2. Two disks

If we have two disks, we have to some series of steps.
The steps will be following,
- 1 from A to B
- 2 from A to C
- 1 from B to C

3. N disks

If we have disks more than two disks, then it will get complicated.
To know the required moves, following function will be helpful.

import java.util.*;

public class towerofhanoi{
    
    static Scanner s = new Scanner(System.in);
    public static void TowerofHanoi(int n, char A, char B, char C) {
    if(n>0) {
        TowerofHanoi(n-1, A, C, B);
        System.out.println("Move Disk "+n+" from "+A+" to "+C);
        TowerofHanoi(n-1, B, A, C);
        }
    }
    public static void main(String[] args) {
        System.out.println("Enter no. of Disks: ");
        char A = 'A', B = 'B', C = 'C';
        int n = s.nextInt();
        TowerofHanoi(n,A,B,C);
    }
}

For 3 disks

OUTPUT

Enter no. of Disks: 
3
Move Disk 1 from A to C
Move Disk 2 from A to B
Move Disk 1 from C to B
Move Disk 3 from A to C
Move Disk 1 from B to A
Move Disk 2 from B to C
Move Disk 1 from A to C

Time Complexity

Let the time required for n disks is T(n) .
There are 2 recursive call for n-1 disks and one constant time operation to move a disk from 'A' rod to 'C' rod . Let it be k1.

Therefore,

T(n) = 2 T(n-1) + k1
T(0) = k2 , a constant.
T(1) = 2 k2 + k1
T(2) = 4 k2 + 2k1 + k1
T(2) = 8 k2 + 4k1 + 2k1 + k1
Coefficient of k1 =2n
Coefficient of k2 =2n-1

Time complexity is O(2^n) or O(a^n) where a is a constant greater than 1.
So it has exponential time complexity.
For single increase in problem size the time required is double the previous one.
This is computationally very expensive. Most of the recursive programs takes exponential time that is why it is very hard to write them
iteratively .

Worst Case Time Complexity

The worst case is when no. of disks are N. As it is unknown and assumed to be very large.
For Example, the disks are like 1, 2, 3, ... N.

Worst Case : 1, 2, 3, 4, .....N
Time Complexity :  2^N - 1

It will be BigO(2^N)

Best Case Time Complexity

There is no best case as the starting and end point of this problem is same. If value of N is reduced (like N=1), it performs better.

So, it will be BigO(2^N)

Average Case Time Complexity

The average case is when no. of disks is N as same as the worst case.
It is also unknown and assumed to be very large.
The time complexity will be BigO(2^N).
For Example:

If no. of disks is equal to 
    10     --> 1023
    20     --> 1048575
    100    -->  1.2676e30 which is very large

Space Complexity

Space for parameter for each call is independent of n i.e., constant.
Let it be k .When we do the 2nd recursive call 1st recursive call is over . So, we can reuse the space of 1st call for 2nd call .
Hence ,

T(n) = T(n-1) + k
T(0) = k
T(1) = 2k
T(2) = 3k
T(3) = 4k

So the space complexity is O(n).

Conclusion

The following table shows the Space & Time Complexities of Tower of Hanoi problem:

Where N is the input size.

Name of the Complexity	in BigO
Worst Case Time Complexity	O(2^N)
Average Case Time Complexity	O(2^N)
Best Case Time Complexity	O(2^N)
Space Complexity	O(N)

The Time complexity of the Tower of Hanoi problem is O(2^n), where n is the number of discs. This is because the algorithm recursively solves two subproblems of size n-1 at each step, and the number of steps required to solve a problem of size n is equal to 2^n - 1.
The Space complexity of the Tower of Hanoi problem is O(n), where n is the number of discs. This is because the algorithm uses a recursive approach and at any point of time, it needs to keep track of n discs and three rods which are used for moving the discs.

Time & Space Complexity of Tower of Hanoi Problem

Algorithms