In this article, we will demonstrate how to implement 2 stacks in one array. Both stacks are independent but use the same array. We need to make sure one stack does not interfere with the other stack and support push and pop operation accordingly.

The topics we have covered in this article at OpenGenus are as follows:

• Introduction to stack & array
• Implement 2 stack in 1 array
  • Approach 1: Divide array in 2 parts
  • Approach 2: Space efficient approach

Introduction

Stack

Stack is an abstract data type with a bounded capacity. It is a simple data structure that allows adding and removing elements in a particular order. Every time an element is added, it goes on the top of the stack and the only element that can be removed is the element that is at the top of the stack, just like a pile of objects.

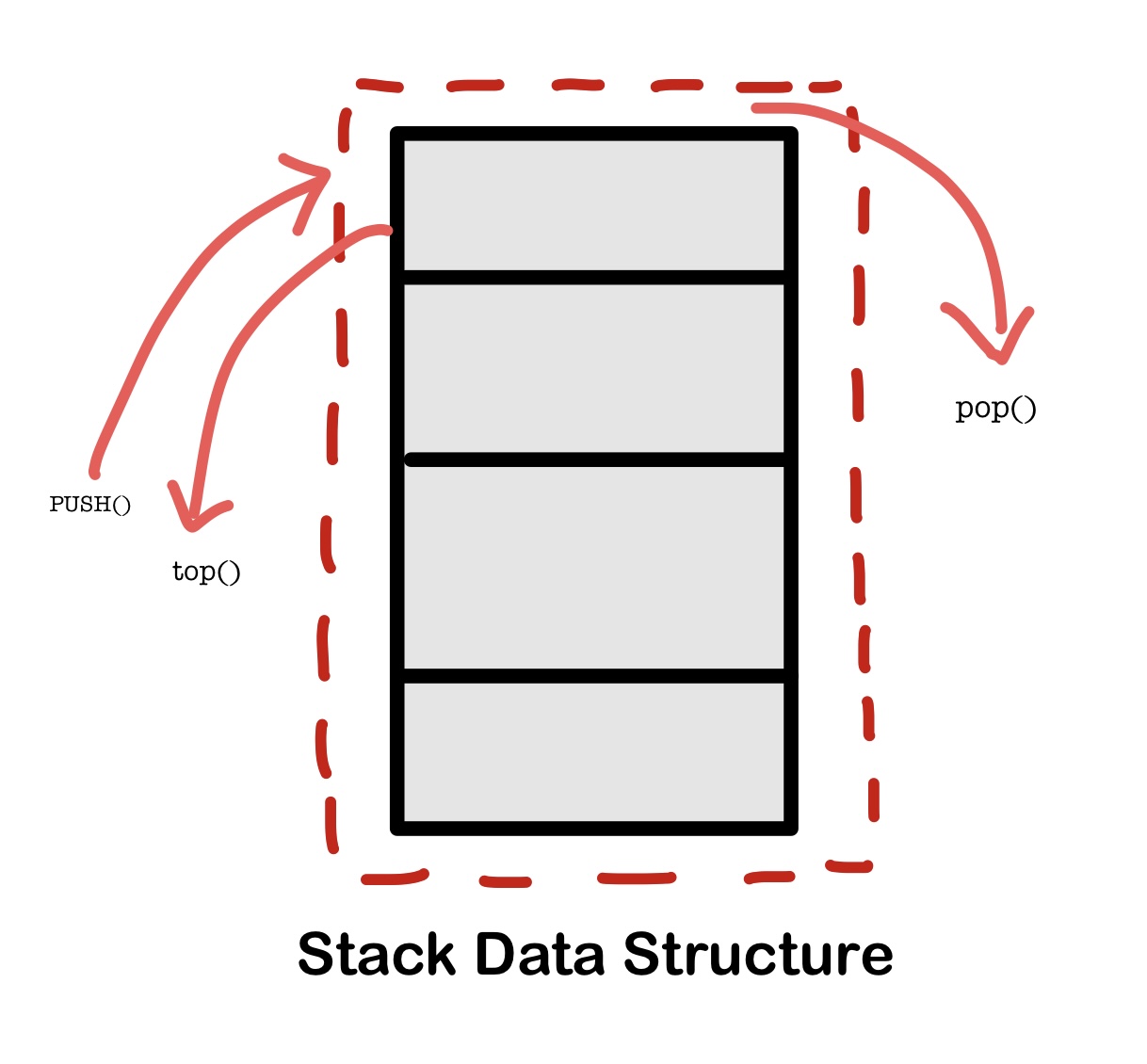
Implementation of Stack Data Structure

Stack can be easily implemented using an Array or a Linked List. Arrays are quick, but are limited in size and Linked List requires overhead to allocate, link, unlink, and deallocate, but is not limited in size. Here we will implement Stack using array.

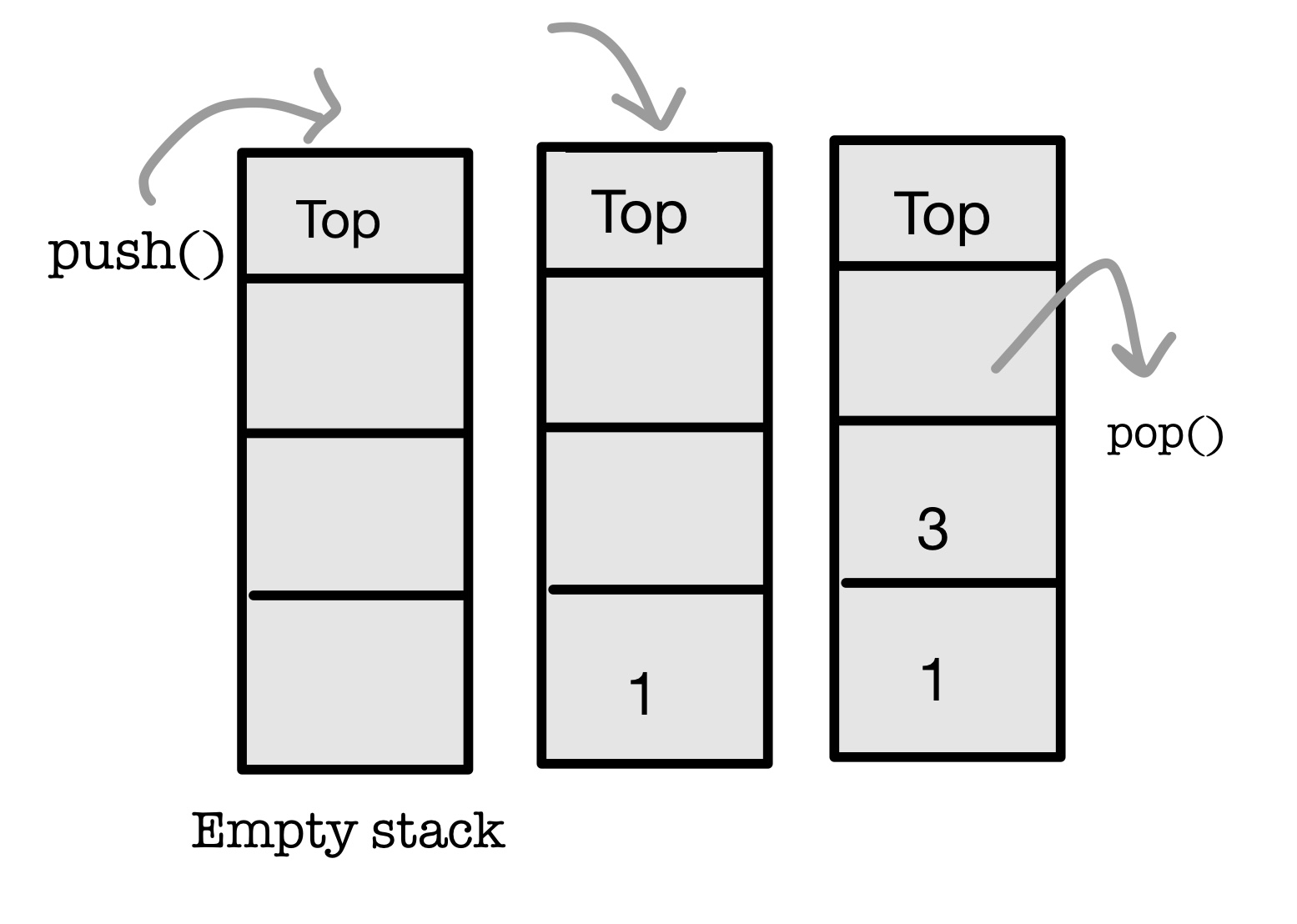
Algorithm for PUSH operation

• Check if the stack is full or not.
• If the stack is full, then print error of overflow and exit the program.
• If the stack is not full, then increment the top and add the element.

Push(S,x)
if Stack-Full(S)
    then error "overflow"
else top(S) = top(S) + 1
    S[top(S)] = S

Algorithm for POP operation

• Check if the stack is empty or not.
• If the stack is empty, then print error of underflow and exit the program.
• If the stack is not empty, then print the element at the top and decrement the top.

Pop(S)
if Stack-Empty(S)
    then error "underflow"
else top(S) = top(S) - 1
    return S[top(S) + 1]

Arrays
The array is a fixed-size sequenced collection of variables belonging to the same data types. The array has adjacent memory locations to store values.
The syntax for declaring array are:

data_type array_name [array_size];

Basic Operations

There is some specific operation that can be performed or those that are supported by the array. These are:

1. Traversing: It prints all the array elements one after another.
2. Inserting: It adds an element at given index.
3. Deleting: It is used to delete an element at given index.
4. Searching: It searches for an element(s) using given index or by value.
5. Updating: It is used to update an element at given index

2 stacks in 1 array

Now Let's start with our task for Implementing two stacks in one array

Algorithmic Approach

The steps to implement two stacks in one array are:

• Given an array of integers.
• Create two stacks using single array.
• We shall able to perform push & pop operations on both stacks.
• We will create two stacks i.e. stack1 and stack2.
• stack1 will have following methods.
  1. push1 method: push1 method will insert the element to stack1
  2. pop1 method: pop1 method will remove the top element from stack1.
• stack2 will have following methods.
  1. push2 method: push2 method will insert the element to stack2.
  2. pop2 method: pop2 method will remove the top element from stack2.

Working of Push and Pop

1.PUSH function will take the stack name and value to be inserted, and pushes the number into respective stack

• According to the stack name proceed
• Check whether the stack is full or not ie, top1 < top2 -1 Here, top1, top2 are the variables to keep track of top elements in both stacks
• If not, push the element in the respective stack ie, arr[top1] = k

2. POP will take the stack name and will pop the topmost element in that stack

• According to the stack name proceed
• Check whether their is any element to pop
• If yes, decrement or increment the top1, top2 varaibles accordingly

There are basically 2 ways in which we can do this problem statement :

1. Divide and Space into two halves
2. Space efficient implementation

Method 1: Divide and Space into two halves

The simplest way is to implement two stacks in an array is by dividing the array into two equal halves and using these halves as two different stacks to store the data.

This method works fine, however, it is not space-efficient because suppose we have two stacks with 4 and 6 elements and our array is of 10 lengths. Now, if we divide our array into two equal halves then it is going to have two stacks of length 5. If we push only 4 items in the first stack then it has one space vacant and when we try to push 6 items in the second stack it will overflow because it only has a capacity of 5. We could have used the 1 vacant space of the first stack to store the data.

Simple Algorithm

1. We will divide the input array into two equal sub arrays. Left stack from index 0 to N/2-1 and right stack from index N/2 to N-1.
2. Left stack will start from index 0 and can go till index N/2-1 whereas right start will start from index N/2 and can go till index N-1.
3. Any stack cannot hold more than N/2 elements.

For example, take an array of size 6.

element1	element2	element3	element4	element5	element6
-	-	-	-	-	-

The above array needs to support two stacks so we will divide it into two equal parts each having 3 elements. It is as follows:

Array part 1:

element1	element2	element3
-	-	-

Array part 2:

element4	element5	element6
-	-	-

Note the division into two parts is logical and it exists as one single array in actual implementation. See how the operations are performed:

Push "10" in Stack 2:

element1	element2	element3	element4	element5	element6
-	-	-	10	-	-

[ Add some steps of push and pop in stack 1 and stack 2]

Complexity Analysis:
Time Complexity
Push operation : O(1)
Pop operation : O(1)
Auxiliary Space: O(N).
Use of array to implement stack so. It is not the space-optimised method as explained above.

So to overcome this problem we use Space efficient implementation method.

Method 2 : Space efficient implementation

This method is very space-efficient and it does not overflow if there is space available in the array or any of the stack.The concept we use here is we store the data on the two different ends in the array (from start and from end).The first stack stores the data from the front that is at index 0 and the second stack stores the data from the end that is the index ArraySize-1.
Both stack push and pop data from opposite ends and to prevent the overflow we just need to check if there is space in the array.

Simple Algorithm

• Start with two indexes, one at the left end and other at the right end
• The left index simulates the first stack and the right index simulates the second stack.
• If we want to push an element into the first stack then put the element at left index.
• Similarly, if we want to push an element into the second stack then put the element at the right index.
  First stack goes towards the right and the second stack goes towards left.

Code in JAVA

class TwoStacks { 
    int size; 
    int top1, top2; 
    int arr[]; 
  
    // Constructor 
    TwoStacks(int n) 
    { 
        arr = new int[n]; 
        size = n; 
        top1 = -1; 
        top2 = size; 
    } 
  
    // Method to push an element x to stack1 
    void push1(int x) 
    { 
        // There is at least one empty space for 
        // new element 
        if (top1 < top2 - 1) { 
            top1++; 
            arr[top1] = x; 
        } 
        else { 
            System.out.println("Stack Overflow"); 
            System.exit(1); 
        } 
    } 
  
    // Method to push an element x to stack2 
    void push2(int x) 
    { 
        // There is at least one empty space for 
        // new element 
        if (top1 < top2 - 1) { 
            top2--; 
            arr[top2] = x; 
        } 
        else { 
            System.out.println("Stack Overflow"); 
            System.exit(1); 
        } 
    } 
  
    // Method to pop an element from first stack 
    int pop1() 
    { 
        if (top1 >= 0) { 
            int x = arr[top1]; 
            top1--; 
            return x; 
        } 
        else { 
            System.out.println("Stack Underflow"); 
            System.exit(1); 
        } 
        return 0; 
    } 
  
    // Method to pop an element from second stack 
    int pop2() 
    { 
        if (top2 < size) { 
            int x = arr[top2]; 
            top2++; 
            return x; 
        } 
        else { 
            System.out.println("Stack Underflow"); 
            System.exit(1); 
        } 
        return 0; 
    } 
  
    // Driver program to test twoStack class 
    public static void main(String args[]) 
    { 
        TwoStacks ts = new TwoStacks(5); 
        ts.push1(3); 
        ts.push2(10); 
        ts.push2(17); 
        ts.push1(11); 
        ts.push2(7); 
        System.out.println("Popped element from"
                           + " stack1 is " + ts.pop1()); 
        ts.push2(60); 
        System.out.println("Popped element from"
                           + " stack2 is " + ts.pop2()); 
}
}

Output :
Popped element from stack1 is 11
Popped element from stack2 is 60

Complexity Analysis:
Time Complexity:
Push operation : O(1)
Pop operation : O(1)
Auxiliary Space :O(N).
Use of array to implement stack so it is a space-optimised method.