Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
In history, we have calculated some interesting numbers and theorems which we admire even today. At the same time, there are numbers which were thought to be of extreme significance but eventually, results to be only of historial significance.
Yes, just like how humans reach the pinnacle of success and suddenly fall back to zero, we have some numbers which become a Mathematician's dream number but eventually gets ignored.
It took 91 years and Mathematicians from 3 generations to propose, prove and show a result to be both interesting and dull.
1808
It all started in 1808.
Mathematicians were facinated by prime numbers and their distribution. It was an exciting and significant field of study that eventually lead to Prime Number theorem and visually exciting theorems such as Riemann zeta function, Meissel Lehmer algorithm and many others.
It was widely believed at this time that the number of prime numbers below a given number N follows a fixed pattern. There was no idea how to tackle this but the implications were huge which would explain some of the intuitions like Why prime numbers are found less frequently as we go further down the number line? and many others.
Adrien Marie Legendre was a great mathematician at this time. People usually know him for two major commonly encountered contributions:
- Legendre polynomials
- Legendre transformation
Legendre's name is one of the 72 names inscribed on Eiffel Tower.
Among many of this contributions, a constant was named after him.
B is Legendre's constant. It captures the number of prime numbers below a given number.
Legendre claimed in 1808:
π(N) = N / (ln(N) - B(N))
where:
- π(N) = number of prime numbers less than N
- ln(N) = logarithmic of N with e as base
- B(N) = a constant
Legendre claimed that as N tends to infinity, B(N) which is a constant tends to be about 1.08366 (an irrational number).
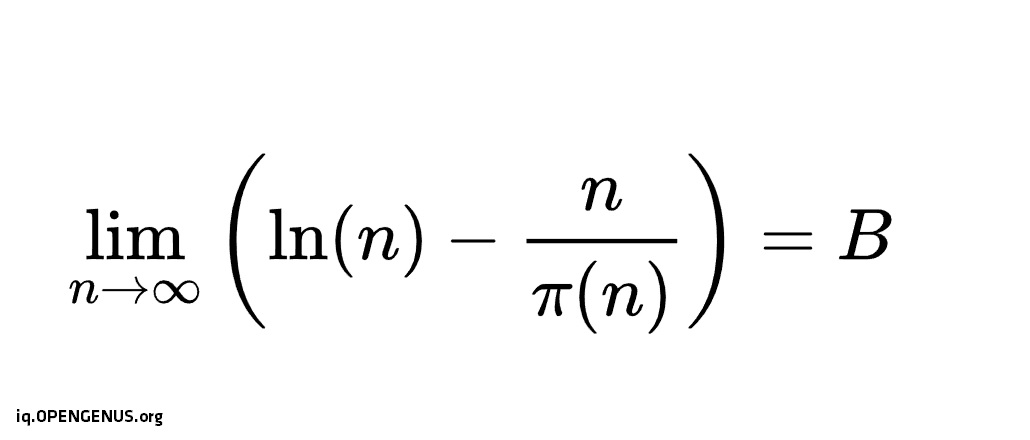
If we plot the value of B for increasing value of N, we get a plot like this which averages to 1.08366...
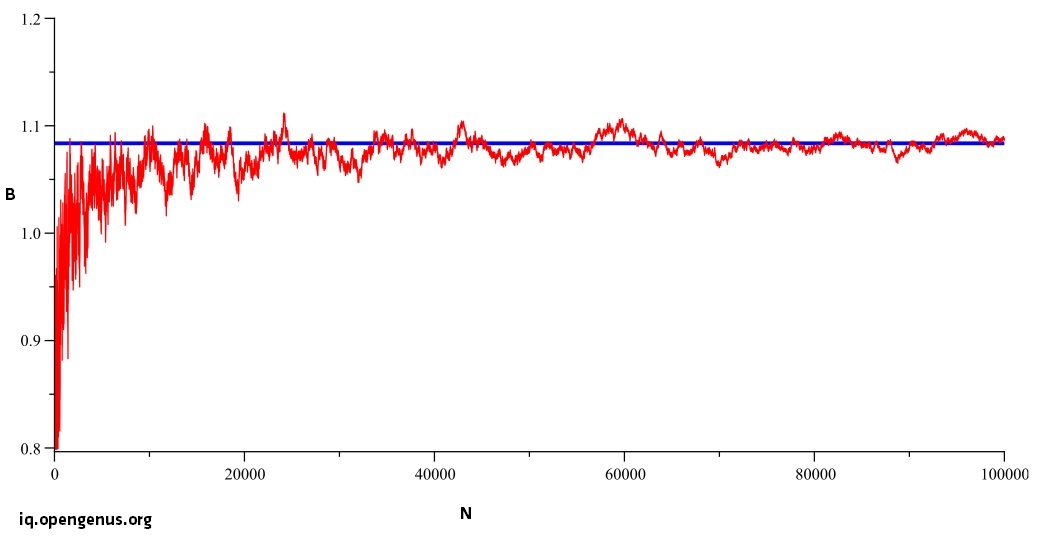
This was also a source of confusing as the plot shows that the value is tending to be stable and little we knew that it will differ largely as we go on to higher values of N.
At this point, the exact value did not matter. It was more important that such a constant exists as it would imply the truth of prime number theorem. Prime Number Theorem defines the distribution of prime numbers across positive numbers.
Mathematicians struggled to find the exact value of B or to prove that B exists but this was a light of hope. Unfornately, Legendre passed away in 1833 after struggling with a painful illness.
1849: cracks started to appear
Pafnuty Chebyshev, another great Mathematician from Russia proved that if such a constant exists, it has to be 1.
This was a cloudy moment in history. Everyone was tensed as it is likely that such a constant does not exist as 1 is considered to be a dull number.
Still, no progress was made and uncertainity continued. Again, Chebyshev passed away in 1894.
1899: complete fall
Charles Jean de la Vallée Poussin proved it once and for all that Legendre's constant exists but it is 1. This was done in 1899 and he is most popularly known for this.
Things were good that prime number theorem is infact true but unfortunately, Legendre's constant is 1 and not 1.08366 which would have been exciting just like values of pie and e.
pie and e are not just mathematical constants. It is much greater and defines the universal structure. Legendre's constant do have the same significance but the overall excitment is reduced as it turned out to be a simple number 1.
Aftermath: 1980 and 2010
People still remember Legendre's constant but the excitment is no longer there and usually, used to denote the historically incorrect value 1.08366.
In 1980, Janos Pintz published an easier proof backing Pafnuty Chebyshev's 1849 work.
In 2010, Pierre Dusart gave an easy proof that B is infact between 1 and 1.1.
In memory of Legendre, we would like to end with Drake's meme: