Home Discussions Write at Opengenus IQ
×

Search anything:

Find point of 2D Line Intersection

Binary Tree book by OpenGenus

Open-Source Internship opportunity by OpenGenus for programmers. Apply now.

Reading time: 40 minutes | Coding time: 5 minutes

Line Intersection co-ordinates are the solution of two corresponding lines taken into consideration in the 2-Dimensional plane. We will cover two algorithms namely:

  • Elimination Method (Method 1)
  • Determinant Method (Method 2)

Both methods take constant time O(1) assuming the multiplication takes O(1) time.

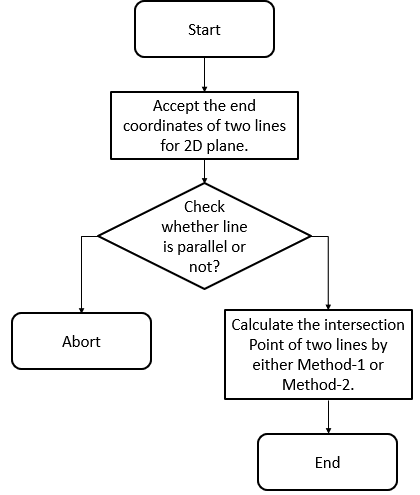
Flowchart

Following flowchart explains the overall process:

FlowChart

Pseudocode of Elimination Method :

  • Step 1 : Input four coordinates of two lines.
  • Step 2 : Compute both the equations in form of ax + by + c = d.
  • Step 3 : Before finding the intersection point coordinate, check whether the lines are parallel or not from the values of slope of each line.
  • Step 4 : To find the values of intersection point, x-coordinate and y-coordinate, eliminate x-coefficient by making it equal in units in both the equations, which would lead to get the value of y coordinate of intersection point.
  • Step 5 : Similarly, to compute x-coordinate eliminate the y-coefficient from both the equations by making their coefficients equal in units which again leads to obtain the x-coordinate of intersection point.

Algorithm of Elimination Method

  • step 1 : Accept the two end coordinates of each for two line segments
    for line-1 : (X1, Y1) & (X2, Y2)
    for line-2 : (X3, Y3) & (X4, Y4)

  • step 2 : Let the equations of lines by two point form be :
    Eq-1 : a1x + b1y = c1;
    Eq-2 : a2x + b2y = c2;
    solving the above equation simultaneously by eliminating the x variable by making its coefficients equal by multipliying Eq-1 by a2 and Eq-2 by a1 and further substracting Eq-2 from Eq-1.

  • step 3 : We will get following Equations,
    Eq-1.1 : a2a1x + a2b1y = a2c1;
    Eq-2.1 : a1a2x + a1b2y = a1c2;
    substracting Eq-2.1 from Eq-1.1.

  • step 4 : After substracting Eq-2.1 from Eq-1.1 we get,
    the value of y-coordinate of intersection point
    y = a1c2 - a2c1 / (a1b2 - a2b1)

  • step 5 : To compute the value of x-coordinate, similar above process has to be carried out.

Example solved by Elimination Method

  • step 1 : following are the coordinates of two lines :
Line-1 : (1, 6) & (2, 5)
Line-2 : (1/3, 8) & (2/3, 7)
  • step 2 : Form the equations

Equation of Line-1 : x + y = 7,
Equation of Line-2 : 3x + y = 9

  • step 3 : Check whether Line-1 and Line-2 are parallel or not.
slope of Line-1 = (5 - 6)/(2 - 1)
                              = -1
slope of Line-2 = (7 - 8)/(2/3 - 1/3)
                              = -3

Here slope of Line-1 an Line-2 are unequal hence they are not parallel.

  • step 4 : solving for intersection of Line-1 and Line-2 for x coordinate,
    as here coefficient of y is already same of both the lines, substracting Line-2 from Line-1 we get,
    * 3x - x = 9 - 7
    * 2x = 2
    * x = 1

substituting x = 1 in Line 1 we get value of y = 6.

  • step 5 : Hence intersection of Line-1 and Line-2 is (1, 6)

Implementation of Elimination Method

#include <iostream>        
#include <vector> 
class EliminationMethd2DLineIntersection
{
public:
    void acceptTheCoordinates(double x1, double y1, double x2, double y2, double x3, double y3, double x4, double y4);
    void intersection1(double x1, double y1, double x2, double y2, double x3, double y3, double x4, double y4);
private:
    std::vector<double> a, b, c, d;    //four coordinates constituting 2 Dimensional Lines.
};
void EliminationMethd2DLineIntersection::acceptTheCoordinates(double x1, double y1, double x2, double y2, double x3, double y3, double x4, double y4)
{
    a.push_back(x1);
    a.push_back(y1);
    b.push_back(x1);
    b.push_back(y1);
    c.push_back(x1);
    c.push_back(y1);
    d.push_back(x1);
    d.push_back(y1);
    intersection1(a[0], a[1], b[0], b[1], c[0], c[1], d[0], d[1]);
}
void EliminationMethd2DLineIntersection::intersection1(double x1, double y1, double x2, double y2, double x3, double y3, double x4, double y4)
{
    double x12 = x1 - x2;
    double x34 = x3 - x4;
    double y12 = y1 - y2;
    double y34 = y3 - y4;
    double c = x12 * y34 - y12 * x34;
    double a = x1 * y2 - y1 * x2;
    double b = x3 * y4 - y3 * x4;
    if(c != 0)
    {
        double x = (a * x34 - b * x12) / c;
        double y = (a * y34 - b * y12) / c;
        std::cout << "Intersection point coordinates : \n";
        std::cout << "Xin : " << x << std::endl;
        std::cout << "Yin : " << y << std::endl;
    } 
    else
    {
        std::cout << "Lines are parallel";
    }
}
int main()
{
    EliminationMethd2DLineIntersection obj;
    int value;
    double x1, y1, x2, y2, x3, y3, x4, y4, x5, y5, x6, y6, x7, y7, x8, y8;
    std::cout << "\nEnter the Coordinates for Line-1";
    std::cout << "\nEnter the X-coordinate for Point-1: ";
    std::cin >> x1;
    std::cout << "\nEnter the Y-coordinate for Point-1: ";
    std::cin >> y1;
    std::cout << "\nEnter the X-coordinate for Point-2: ";
    std::cin >> x2;
    std::cout << "\nEnter the Y-coordinate for Point-2: ";
    std::cin >> y2;
    std::cout << "\nEnter the Coordinates for Line-2";
    std::cout << "\nEnter the X-coordinate for Point-1: ";
    std::cin >> x3;
    std::cout << "\nEnter the Y-coordinate for Point-1: ";
    std::cin >> y3;
    std::cout << "\nEnter the X-coordinate for Point-2: ";
    std::cin >> x4;
    std::cout << "\nEnter the Y-coordinate for Point-2: ";
    std::cin >> y4;
    obj.acceptTheCoordinates(x1,y1, x2, y2, x3, y3, x4, y4);
    return 0;
}

Input:

Enter the Coordinates for Line-1
Enter the X-coordinate for Point-1: 0

Enter the Y-coordinate for Point-1: 0

Enter the X-coordinate for Point-2: 1

Enter the Y-coordinate for Point-2: 2

Enter the Coordinates for Line-2
Enter the X-coordinate for Point-1: 0

Enter the Y-coordinate for Point-1: 6

Enter the X-coordinate for Point-2: 1

Enter the Y-coordinate for Point-2: 5

Output:

Intersection point coordinates : 
Xin : 2
Yin : 4

Determinant Method

Now, we will explore the second approach of finding the intersection of two points using Determinant Method.

Pseudocode of Determinant Method

  • Step 1 : Input four coordinates of two lines.
  • Step 2 : Compute both the equations in form of ax + by + c = d.
  • Step 3 : Before finding the intersection point coordinate, check whether the lines are parallel or not by ensuring if determinant is zero lines are parallel.
  • Step 4 : To find the values of intersection point, x-coordinate and y-coordinate, apply the formulas mentioned in the figure given below.
  • Step 4.1 : The formulas given in figure below are calculated by using technique known elimination, where to compute x-coordinate of intersection we have to eliminate y-coordinate from both the equations we have build in Step 2 so far by, making the coefficients equal of y-coordinate in both the equations. Similarly formula for y-coordinate of intersection is computed by eliminating x-coordinating making x-coordinate coefficients equal in both the equations.
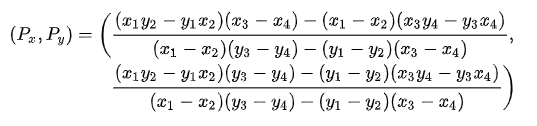
Determinant Method

Algorithm of Determinant Method

Following is the computation to calculate the x and y coordinate of intersection point by Determinant Method.

  • step 1 : Equation of Lines by two point form is given by in ax + by + c = 0,
    Eq 1 : (y2 - y1)x - (x2 - x1)y = x1y2 - x2y1
    Eq 2 : (y4 - y3)x - (x4 - x3)y = x3y4 - x4y3

    By using cramer's rule on above equation we get,

Determinant Method

  • step 2 : Intersection coordinates :
    Explaning cramer's rule in solving above Eq 1 and Eq 2

  • step 2.1 : Solving Eq 1 and Eq 2 for y value, multiply Eq 1 by (y4 - y3) and multiply Eq 2 by (y2 - y1).

  • step 2.2 : After following step 2.1 we get,
    Eq 1.1 : (y4 - y3) (y2 - y1)x - (y4 - y3) (x2 - x1) y = (y4 - y3) (x1y2 - x2y1)
    Eq 2.2 : (y2 - y1) (y4-y3) x - (y2 - y1) (x4 - x3) y = (y2 - y1) (x3y4 - x4y3)

  • step 2.3 : Substracting Eq 2.2 from Eq 1.1 we get,
    y = (y4 - y3) (x1y2 - x2y1) - (y2 - y1) (x3y4 - x4y3) / ((y4 - y3) (x2 - x1) - (y2 - y1) (x4 - x3))

  • step 2.5 : similarly value for x coordinate would be calculated.

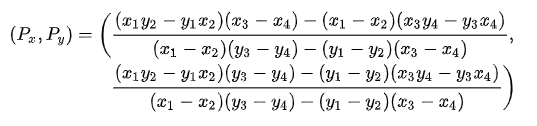
Determinant Method

Example solved by Determinant Method

step 1 : Following are the coordinates of :

Line 1 : (1, 4) & (2, 5)
Line 2 : (1, 10) & (0, 12)

step 2 : Computing Equations of above lines are:

Line 1 : x - y + 3 = 0
Line 2 : 2x + y - 12 = 0

step 3 : Computing determinant to check whether lines are parallel or not.

determinant = (1) * (1) - (-1) * (2)
    * = 1 + 2
    * = 3

where determinant is non-zero meaning lines are not parallel.

step 4 : By applying the formulae for x and y coordinates given above in figure in method-2 algorithm, the intersection point (xin, yin) = (3, 6)

Implementation of Determinant Method

#include <iostream>
class TwoDimensionalLineIntersection
{
public:
    bool determinantMethod();
    void setCoordinatesOfLines(double x1_, double y1_, double x2_, double y2_, double x3_, double y3_, double x4_, double y4_);
    void printIntersectionPoints();
private:
    double x1_, y1_, x2_, y2_, x3_, y3_, x4_, y4_, xin_, yin_;
};
void TwoDimensionalLineIntersection :: setCoordinatesOfLines(double x1_, double y1_, double x2_, double y2_, double x3_, double y3_, double x4_, double y4_)
{
    this->x1_ = x1_;
    this->x2_ = x2_;
    this->x3_ = x3_;
    this->x4_ = x4_;
    this->y1_ = y1_;
    this->y2_ = y2_;
    this->y3_ = y3_;
    this->y4_ = y4_;
}
bool TwoDimensionalLineIntersection :: determinantMethod()
{
    double slopeOfLine1;
    double slopeOfLine2;
    if(x2_ - x1_ != 0)
        slopeOfLine1 = (y2_ - y1_)/(x2_ - x1_);
    else
        slopeOfLine1 = 0;
    if(x4_ - x3_ != 0)
        slopeOfLine2 = (y4_ - y3_)/(x4_ - x3_);
    else
        slopeOfLine1 = 0;
    if(slopeOfLine1 != slopeOfLine2)
    {
        xin_ = ((x1_*y2_ - y1_*x2_)*(x3_ - x4_) - (x3_*y4_ - y3_*x4_)*(x1_ - x2_) )/( ((x1_ - x2_)*(y3_ - y4_))- ((y1_ - y2_)*(x3_ - x4_)));
        yin_ = ((x1_*y2_ - y1_*x2_)*(y3_ - y4_) - (x3_*y4_ - y3_*x4_)*(y1_ - y2_) )/( ((x1_ - x2_)*(y3_ - y4_))- ((y1_ - y2_)*(x3_ - x4_)));
        return true;
    } 
    else
        return false;
}
void TwoDimensionalLineIntersection ::printIntersectionPoints()
{
    if(determinantMethod())
    {
        std::cout << "\nIntersection Coordinate : ";
        std::cout << "\nX-coordinate : " << xin_;
        std::cout << "\nY-coordinate : " << yin_;
    } else
        std::cout << "\nLines are Parallel.";
}
int main()
{
    TwoDimensionalLineIntersection t;
    double x1, y1, x2, y2, x3, y3, x4, y4;
    std::cout << "\nEnter the Coordinates for Line-1 : ";
    std::cout << "\nLine-1 | x1-coordinate : ";
    std::cin >> x1;
    std::cout << "\nLine-1 | y1-coordinate : ";
    std::cin >> y1;
    std::cout << "\nLine-1 | x2-coordinate : ";
    std::cin >> x2;
    std::cout << "\nLine-1 | y2-coordinate : ";
    std::cin >> y2;
    std::cout << "\nEnter the Coordinates for Line-2 : ";
    std::cout << "\nLine-2 | x3-coordinate : ";
    std::cin >> x3;
    std::cout << "\nLine-2 | y3-coordinate : ";
    std::cin >> y3;
    std::cout << "\nLine-2 | x4-coordinate : ";
    std::cin >> x4;
    std::cout << "\nLine-2 | y4-coordinate : ";
    std::cin >> y4;
    t.setCoordinatesOfLines(x1, y1, x2, y2, x3, y3, x4, y4);
    t.printIntersectionPoints();
}

Input:

Enter the Coordinates for Line-1 : 
Line-1 | x1-coordinate : 0
Line-1 | y1-coordinate : 0
Line-1 | x2-coordinate : 1
Line-1 | y2-coordinate : 2
Enter the Coordinates for Line-2 : 
Line-2 | x3-coordinate : 0
Line-2 | y3-coordinate : 6
Line-2 | x4-coordinate : 1
Line-2 | y4-coordinate : 5

Output:

Intersection Coordinate : 
X-coordinate : 2
Y-coordinate : 4

Complexity

The time and space complexity of finding Intersection point of 2D Lines by Determinant Method are:

  • Worst case time complexity: Θ(1)
  • Average case time complexity: Θ(1)
  • Best case time complexity: Θ(1)
  • Space complexity: Θ(1)
—
Find point of 2D Line Intersection
Share this