
Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
In this article, we discuss about how to find the Prefix sum of a given matrix that is 2D Prefix Sum. We have demonstrated 3 methods to find the 2D prefix sum.
Table of Content
- Problem Statement
- Explanation
- Approach 1
- Approach 2
- Approach 3
- Related Problems
Problem Statement:
We are given an 2D array or a nxn Matrix and we are required to find the prefix sum of that given array.
Explanation:
Let us consider a matrix m[r][c] and p[r][c] be the prefix sum matrix where r is no. of rows and c is no. of columns respectively. Now, the p[i][j] of prefix sum matrix is equal to the sum of [i][j] element and sum of all the elements before and equal to ith row and jth column of the given matrix.
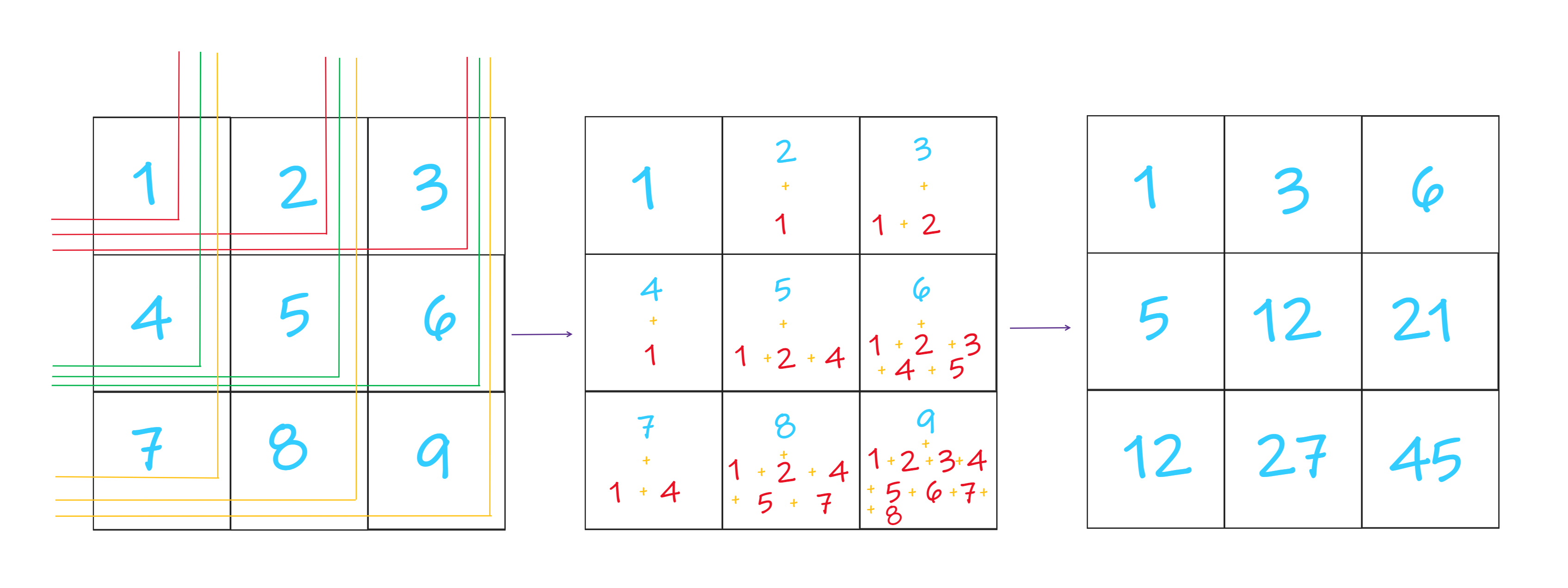
Approach 1
- It's a Brute force approach.
- Calculate the prefix sum of each index individually.
- For [i][j]th index calculate the sum of all the elements by traversing all the elements less than equal to [i][j]th index horizontally and vertically.
- The resultant matrix is our solution.
Code:
#include<bits/stdc++.h>
using namespace std;
int main() {
// Input the Array
int r,c;
cin>>r>>c;
vector<vector<int>> v(r, vector<int>(c));
for(int i=0;i<r;i++) {
for(int j=0;j<c;j++) {
cin>>v[i][j];
}
}
// Calculation of prefix sum
vector<vector<int>> ans = v;
for(int i=0;i<r;i++) {
for(int j=0;j<c;j++) {
int sum = 0;
for(int k=0;k<=i;k++) {
for(int l=0;l<=j;l++) {
sum += v[k][l];
}
}
ans[i][j] = sum;
}
}
// Output the answer
for(int i=0;i<r;i++) {
for(int j=0;j<c;j++) {
cout<<ans[i][j]<<' ';
}
cout<<endl;
}
}
Input
3 3
1 2 3
4 5 6
7 8 9
Output:
1 3 6
5 12 21
12 27 45
Time Complexity: O(r^2 * c^2)
As we are running four nested for loop to calculate the prefix sum of each element of the given matrix.
Space Complexity: O(r * c)
As we use a new matrix to store the prefix sum of each element of the given array.
Approach 2
- This approach is optimised solution of above the above one.
- Firstly, calculate the sum of [i][j]th index by traversing all the element less than and equal to [j]th index i.e the same row.
- Secondly, calculate the sum of [i][j]th index by traversing all the element less than and equal to [i]th index i.e the column row.
- The resultant matrix is the required matrix.
Code:
#include<bits/stdc++.h>
using namespace std;
int main() {
// Input the Array
int r,c;
cin>>r>>c;
vector<vector<int>> v(r, vector<int>(c));
for(int i=0;i<r;i++) {
for(int j=0;j<c;j++) {
cin>>v[i][j];
}
}
// Prefix sum of each row elements
for(int i=0;i<r;i++) {
for(int j=1;j<c;j++) {
v[i][j] += v[i][j-1];
}
}
// Prefix sum of each column elements
for(int i=1;i<r;i++) {
for(int j=0;j<c;j++) {
v[i][j] += v[i-1][j];
}
}
// Output the array
for(int i=0;i<r;i++) {
for(int j=0;j<c;j++) {
cout<<v[i][j]<<' ';
}
cout<<endl;
}
}
Input
3 3
1 2 3
4 5 6
7 8 9
Output:
1 3 6
5 12 21
12 27 45
Time Complexity: O(2 * r * c)
As we are traversing all the elements of the Matrix one for finding row prefix and other for column prefix sum.
Space Complexity: O(1)
No extra space is required.
Approach 3
- In this approach we will use Dynamic Programming.
- Here the 2D matrix's first row will prefix sum of first row of given array.
- first column will be the prefix sum of first column of given array.
- After that, [i][j]th element of the matrix will be equal to [i][j-1]th + [i-1][j]th - [i-1][j-1]th elements.
- In this way will we get the prefix sum of the 2D array.
Code:
#include<bits/stdc++.h>
using namespace std;
int main() {
//Input
int r,c;
cin>>r>>c;
vector<vector<int>> v(r, vector<int>(c));
for(int i=0;i<r;i++) {
for(int j=0;j<c;j++) {
cin>>v[i][j];
}
}
// First row prefix sum
for(int i=1;i<c;i++) {
v[0][i] += v[0][i-1];
}
// First column prefix sum
for(int i=1;i<r;i++) {
v[i][0] += v[i-1][0];
}
// Resultant Array
for(int i=1;i<r;i++) {
for(int j=1;j<c;j++) {
v[i][j] += v[i-1][j]+v[i][j-1]-v[i-1][j-1];
}
}
//Output
for(int i=0;i<r;i++) {
for(int j=0;j<c;j++) {
cout<<v[i][j]<<' ';
}
cout<<endl;
}
}
Input
3 3
1 2 3
4 5 6
7 8 9
Output:
1 3 6
5 12 21
12 27 45
Time Complexity: O(r * c)
As we are traversing all the elements of the Matrix.
Space Complexity: O(1)
No extra space is required.
Related Problems
- To make prefix sum array product non-zero by arranging the array.
In this problem we have arrange the array such that the prfix sum of each element is not zero and after rearranging the array we have to output the product of prefix sum. - To find maximum prefix sum such that the sum is equal to suffix sum and suffix and prefix sum doesn't overlap.
In this problem, Along with prefix sum we find suffix sum also. The Approach for suffix sum is similar to prefix sum. We find the maximum suffix and prefix sum such that they are equal and also they don't overlap. - To find prefix factorials of prefix sum Array.
This problem is similar to prefix sum. Here in place of finding sum we find out the products of elements.
With this article at OpenGenus, you must have the complete idea of 2D Prefix Sum.
