
Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
HashMap<K V> in java.util package implements the Map interface in java collection based on Hashtable, where K is the type of the keys and V is the type of the mapped value. It allows users to store key-value pair, where no duplicate keys are allowed. Order is not maintained as well.
There are three main applications of Hash Map:
- Priority Queues
- Dijkstra's Algorithm
- Topological Sort
However, unlike Hashtable, it allows us to store null elements. Hence, the elements of a Hashmap could be:
- key-value
- null-null
- key-null
- null-value
Note that only one null key is allowed. Also, we can't use method get() to judge whether the Hashmap contains certain key since the map may contain a null key. Instead, containsKey() shoud be adopted.
Common Methods and Initialization
initialization:
Map<String, Integer> map = new HashMap<>();
Some of the most often used methods are:
- V put(K key, V value): Insert a key-value pair to the map. Often used to update values. Returns the previous value mapped to the key, or null if there was no previous mapping.
- boolean containsKey(Object key): Return true if the map contains the key or false otherwise
- V get(Object key): Return the corresponding value of the key in the Hashmap
- V remove(Object key): Remove the key-value pair associated with this key in the Hashmap and return the value to which the key is mapped
The time complexity of the methods above are all ideally O(1) in general. Hence, it is evident that the most significant advantage of this implementation of Map interface is that it allows for amortized constant time retrieval and insertion of data.
However, the prerequisite of using HashMap is that we can associate our data with a particular key(i.e. we can express our data in the form of key-value pair). Some may argue that ArrayList also allows for amortized constant time access and insertion. The key difference is that ArrayList prvides an index-based operation of data and the adoption of HashMap is preferred when index-based mapping of data is indirect and tedious to maintain.
In conclusion, we normally use HashMap when our major demand is merely accessing, modifying, or deleting data based on Key. For instance, in an application we might want to retrieve information of a user by using the username. Then the use of hashmap is preferred as there is need for fast information retrieval and a one-to-one mapping exist.
In the following paragraph, I will demonstrate the usage of Hashmap in implementing several data structures and algorithms.
Implementing Priority Queues
A priority queue is an abstract data type in which each element is assigned a priority. The element of the highest priority always appears at the front of the queue.
Here we will demonstrate implementing a priority queue using binary heap. The elements inside a priority queue are only sorted partially, with the "parent" node being more important than both of its "child" nodes. The implementation of heap is based on array. Given that the heap is a complete tree, children of node k are nodes 2k+1 and 2k+2 and parent of node k is node (k-1)/2. For example, in the min heap priority queue demonstrated by the fugure below (the smallest number 1 appears in the front), node 1 (the node of value 3) has its children in position 2+1 = 3 and 2+2 = 4 in the array.
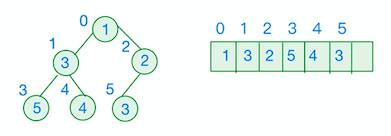
In our implementation of priority queue, we use hashmap to store an element's position in the array as the key and its information about its value and priority as the corresponding value.
import java.util.HashMap;
public class Heap<T> {
protected Item[] c;
protected int size;
protected HashMap<T, Integer> map;
public Heap(boolean isMin) {
isMinHeap= isMin;
c= (Item[]) Array.newInstance(Item.class, 16);
map= new HashMap<>();
}
/** An object of class Item houses a value and a priority. */
class Item {
protected T value; // The value
protected double priority; // The priority
/** An instance with value v and priority p. */
protected Item(T v, double p) {
value= v;
priority= p;
}
/** Add v with priority p to the heap. <br>
* Throw an illegalArgumentException if v is already in the heap. **/
public void add(T v, double p) throws IllegalArgumentException {
if (map.containsKey(v) != null) { throw new IllegalArgumentException(); }
fixCapacity();
Item a= new Item(v, p);
c[size]= a;
map.put(v, size);
size++ ;
bubbleUp(size - 1);
}
/** If h >= size, return.<br>
* Otherwise, bubble c[h] up the heap to its right place.*/
void bubbleUp(int h) {
int p= (h - 1) / 2;
while (h > 0 && compareTo(h, p) == 1){
swap(h, p);
h= p;
p= (h - 1) / 2;
}
}
public int compareTo(int h, int k) {
return compareTo(c[h].priority, c[k].priority);
}
/** Swap c[h] and c[k]. */
void swap(int h, int k) {
assert 0 <= h && h < size && 0 <= k && k < size;
Item i= c[h];
c[h]= c[k];
c[k]= i;
map.put(c[h].value, h);
map.put(c[k].value, k);
}
The advantage of using HashMap is clear. When adding elements to the priority queue, we need to modify the position of the nodes above each time we "bubbleUp" the node we want to insert. Since we are modifying data frequently, it is preferred to make this operation constant time.
Implementing Dijkstra's Algorithm
the nodes are partitioned into three sets:
- settled set S. for each node in this set, the shortest distance from the source node is known.
- frontier set F: nodes that have been visited at least once. Shortest distance from the source node to each of these nodes is known over paths that were traversed but shorter path might haven't been discovered .
- far-off set:nodes that haven’t been visited yet
In each iteration of of the Dijkstra's algorithm, we add the node with shortest distance to source node in the frontier set F to the settled set and update the neighboring nodes' distance and backpointer if nececessary.
Thus, we need to have access to the current distance of all the neighboring nodes and may modify their backpointers and distances in each iteration, making declaring a HashMap to contain these information an optimum choice.
import java.util.HashMap;
public static List<Node> shortestPath(Node v, Node last) {
// Contains an entry for each node in the frontier set.
// The priority of a node is the length of the shortest known path
// from v to the node using only settled node except for the last
// node, which is in F
Heap<Node> F= new Heap<>(true);
// Contains an entry for each node in the settled and frontier set.
// The keys of the map are the nodes, values are the Nodedata of the
// node, which contains the information about its distance from the
// start node and the backpointer of the node.
HashMap<Node, NodeData> SandF= new HashMap<>();
SandF.put(v, new NodeData(null, 0));
F.add(v, 0);
while (F.size() != 0) {
Node f= F.poll();
if (f.equals(last)) return path(SandF, last);
for (Edge e : f.getExits()) {
Node w= e.getOther(f);
int wdist= SandF.get(f).dist + e.length;
NodeData wData= SandF.get(w);
// if w not in S or F
if (wData == null) {
SandF.put(w, new NodeData(f, wdist));
F.add(w, wdist);
} else if (wdist < wData.dist) {
wData.dist= wdist;
wData.bkptr= f;
F.changePriority(w, wdist);
}
}
}
// no path from v to last
return new LinkedList<>();
}
/** An instance contains information about a node: <br>
* the Distance of this node from the start node and <br>
* its Backpointer: the previous node on a shortest path <br>
* from the first node to this node (null for the start node). */
private static class NodeData {
/** shortest known distance from the start node to this one. */
private int dist;
/** backpointer on path (with shortest known distance) from start node to this one */
private Node bkptr;
/** Constructor: an instance with dist d from the start node and<br>
* backpointer p. */
private NodeData(Node p, int d) {
dist= d; // Distance from start node to this one.
bkptr= p; // Backpointer on the path (null if start node)
}
}
public static List<Node> path(HashMap<Node, NodeData> mapSF, Node last) {
List<Node> path= new LinkedList<>();
Node p= last;
while (p != null) {
path.add(0, p);
p= mapSF.get(p).bkptr;
}
return path;
}
Note: the getExits() method returns a list of edges that directs from node F and the getOther() method of object Edge returns the node on the other end of the edge.
Implementing Topological Sort
Our last example would be implementing topological sort. We want to return a list of nodes in DAG g such that for each edge, its source precedes its sink in the list.
We could find the topological order by understanding the following logic:
- If a node is part of a cycle, there must be an edge directing to it
- Deleting a vertex with indegree zero would not remove any cycles
- Keep deleting vertices with indegree zero and remove all its outgoing edges until no node remains, which means that we need to modify the indegree of neighboring nodes in each iteration. Hence, we use HashMap to associate each node with its indegree for fast data retrieval and modification.
- The order in which we remove the nodes is a topological order, so each time we remove a node we add that to a stack and pop the nodes to an ArrayList that store the result
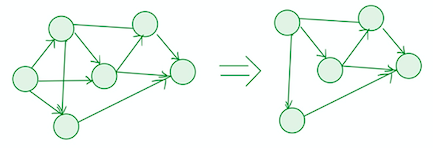
public static List<Node> topologicalSort(Graph g)
int n= g.getNodesSize(); // number of nodes in g
HashSet<Node> nodes= g.getNodes(); // nodes of g
Stack<Node> s= new Stack<>();
HashMap <Node, Integer> indegrees= new HashMap<>();
// Store in s a list of all nodes of indegree 0 and in
// indegrees all nodes with indegree > 0 + their indegrees
for (Node node : nodes) {
int d= node.indegree(); // get the indegree of node
if (d == 0) s.add(node);
else indegrees.put(node, d);
}
List<Node> result= new ArrayList<>();
//contain the list of nodes in topological order
while (s.size() > 0) {
Node node= s.pop();
result.add(node);
List<Node> nn= node.directedNeighbors();
for (Node sink : nn) {
int d= indegrees.get(sink)-1;
if (d == 0) s.push(sink);
else indegrees.put(sink, d); //update indegrees
}
}
}
Conclusion
HashMap is one of the most often used java collection. In general, we use HashMap if the following criteria is satisfied:
- we can form our data into key-value pairs
- we do large amount of operations of retrieving and modifying data with the precondition that the key of the data is easily accessible
