If you are a Machine Learning or Statistics enthusiast, there is hardly any possibility of not hearing the mentioned words - Regression and Correlation. Regression and Correlation are one of the most basic concepts in Statistics and Machine Learning. In this blog we are going to look into what is Regression and Correlation and mainly, the differences between Correlation and Regression.

Key Differences

The key differences between Correlation and Regression:

• Correlation gives a brief summary of relationship between two variables in form of a single point. Regression gives a deeper understanding of the relationship of the dependent variable with other variables in form of a mathematical function
• In correlation the degree and direction of the relation is studied whereas in regression the nature of the relation is studied
• Correlation does not mean Causation but in case of Regression one variable actually affects the other variable according to the function
• Correlation coefficient ranges between -1 and 1. Regression coefficients can take any value
• Correlation is symmetric in nature whereas Regression is assymetric in nature

Correlation

Introduction

According to Wikipedia the definition of correlation is as follows :
In statistics, correlation or dependence is any statistical relationship, whether causal or not, between two random variables or bivariate data
Too technical isn't it !
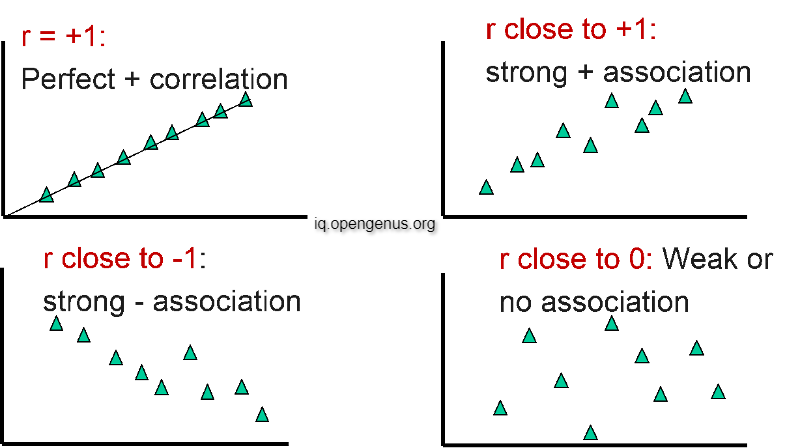
In layman terms correlation is just a statistic that measures the degree to which two variables move in relation to each other. Correlation is measured between two variables using the correlation coefficient. Correlation coefficient ranges between -1 and 1.
Here negative sign represents inverse relation i.e. when one value increases the other decreases and vice-versa.
More is the value of correlation coefficient, stronger is the relation. One thing to observe here is that we only see the magnitude to check the relation strength that means are correlation coefficient of 0.67 is as strong as a correlation coefficient of -0.67.
Please note that Correlation doesn't mean Causation. It may be possible that the the increase/decrease in one variable causes increase/decrease in another variable or maybe some other factor causes both the variables to increase/decrease. We cannot tell this by just looking at the correlation coefficient.

Types of Correlation Coefficient

We are going to discuss the three most popular coefficient of correlations which are as follows :

Pearson r correlation

Pearson r correlation is the most widely used correlation statistic to measure the degree of the relationship between linearly related variables. For example, in the stock market, if we want to measure how two stocks are related to each other, Pearson r correlation is used to measure the degree of relationship between the two. The following formula is used to calculate the Pearson r correlation:

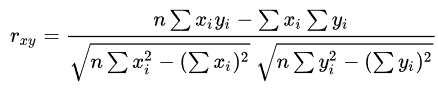
where
rxy = Pearson r correlation coefficient between x and y
n = number of observations
xi = value of x (for ith observation)
yi = value of y (for ith observation)

For the Pearson r correlation, we assume both variables to be normally distributed and satisfy linearity and homoscedasticity

Kendall rank correlation

Kendall rank correlation is a non-parametric test that measures the strength of dependence between two variables. If we consider two samples, a and b, where each sample size is n, we know that the total number of pairings with a b is n(n-1)/2. The following formula is used to calculate the value of Kendall rank correlation:

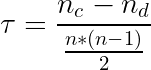
where
n = sample size
Nc= number of concordant
Nd= Number of discordant

Here,Concordant means ordered in the same way and discordant means Ordered differently.
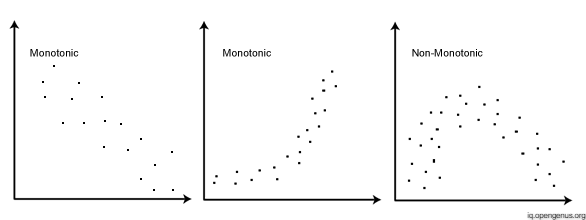
Kendall's rank correlation measures the strength and direction of association that exists (determines if there's a monotonic relationship) between two variables.

Spearman rank correlation

Spearman rank correlation is a non-parametric test that is used to measure the degree of association between two variables. The Spearman rank correlation test does not carry any assumptions about the distribution of the data and is the appropriate correlation analysis when the variables are measured on a scale that is at least ordinal.Formula :

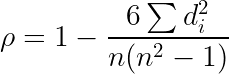
ρ= Spearman rank correlation
di= the difference between the ranks of corresponding variables
n= number of observations
We assign the maxium value Rank 1, second max Rank 2 and so on and do the same for the oher variable and find the sum of all these ranks to find d
The assumptions of the Spearman correlation are that data must be at least ordinal and the scores on one variable must be monotonically related to the other variable

Regression

Regression is a statistical method that attempts to determine the strength and character of the relationship between one dependent variable (usually denoted by Y) and a series of other variables (known as independent variables). Correlation involves only two variables whereas in Regression there is no limit on the number of independent variables
Linear Regression is one of the most important and widely used ML model for predicting continous numerical quantities.

where
Yi = dependent variable
f = function
Xi = independent variable
β = unknown parameters
ei = error terms

We try to predict the relation between the variables by minimizing the error as much as possible.
There are many error functions, but the one mostly used in the Mean Squared Error(MSE)


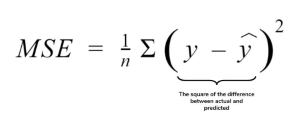
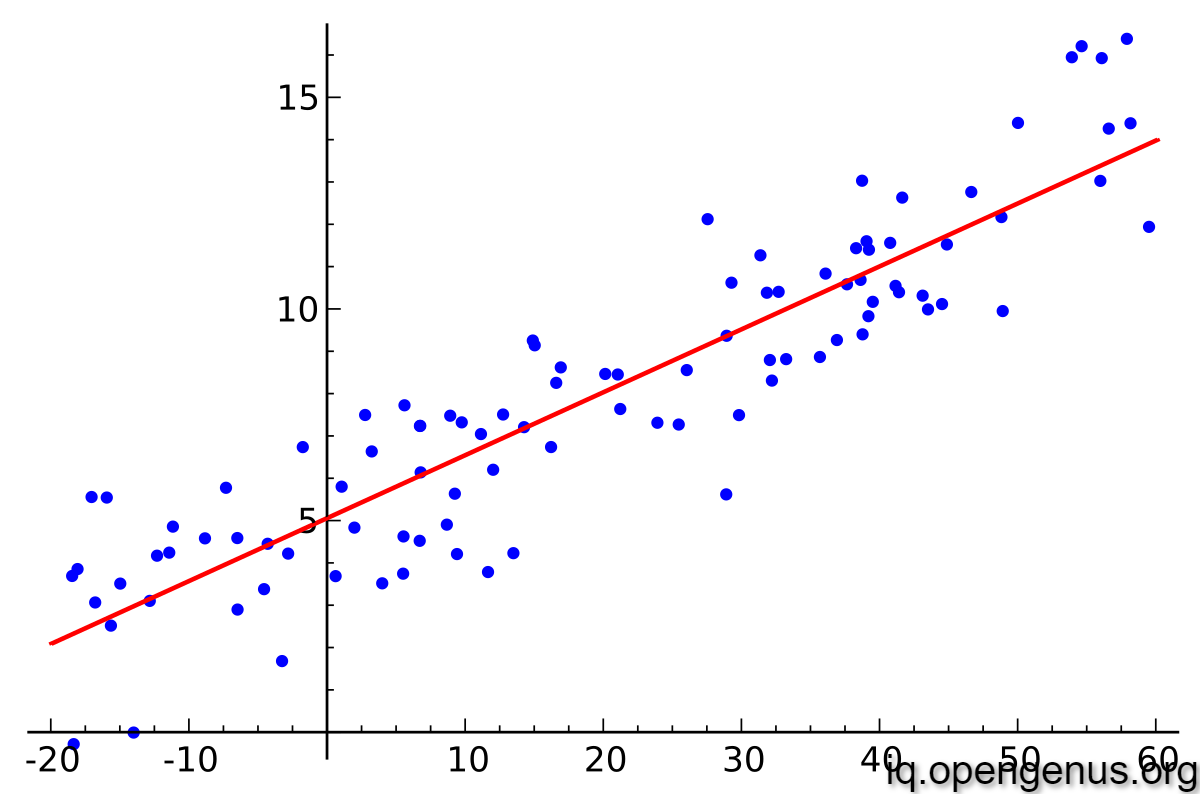
In the above case a line fits our relation the best. Note that this may not always be the case and the relation can be polynomial and not this straight forward
In case of Regression we find a function which estimates our dependent variable the best. Using this function we can predict values of new data. Thus Regression gives more in depth information about the relationship between the variables. We can also interpret the relation further through the Regression function parameters, in case of a straight line throgh the slope and the intercept(there is only one independent variable). The slope tells us the amount of increase in the dependent variable when the indendent variable is increased by one unit. Similary the intercept tells us about the value of dependent variables when independent variable is zero.
For more info on regression please read :
Linear Regression
Logistic Regression
Data Analysis Using Regression
Summary of Regression Techniques
OpenGenus Regression Blogs

Conclusion

We explored Regression and Correlation and found key differences based on the observations. Both Regression and Correlation are one of most important terms in Data Science world !!