
Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
Reading time: 25 minutes
Direct and Logistic regression are generally the main calculations, individuals learn in information science. Because of their fame, plenty of experts even wind up believing that they are the main type of regression. The ones who are marginally increasingly included imagining that they are the most significant among all types of regression analysis.
In all actuality, there are incalculable types of regression, which can be performed. Each structure has its significance and specific conditions where they are most appropriate to apply. In this article, I have clarified the most usually utilized kinds of regressions in information science. Through this article, I likewise trust that individuals build up a thought of the expansiveness of regression, rather than simply applying direct/calculated regression to each issue they go over and trusting that they would simply fit!
Furthermore, in case you are new to information science and searching for a spot to begin your voyage, the 'information science' course is as great a spot as any to begin! Covering the center themes of Python, Statistics and Predictive Modeling, it is the ideal method to step into an information science.
What is Regression Analysis?
Regression Analysis is a type of prescient and parametric demonstrating procedure which predict the connection between a reliant (target) and autonomous variable (s) (indicator). This system is utilized for anticipating, time arrangement displaying and finding the causal impact connection between the factors. For instance, the connection between rash driving and the number of street mishaps by a driver is best concentrated through regression.
Regression Analysis is a significant technique for displaying and breaking down information. Here, we fit a bend/line to the information focuses, in such a way, that the contrasts between the separations of information focus from the bend or line are limited. I'll clarify this in more subtleties in the coming segments.
Sample Regression Line
This is how a simple linear regression line looks like:
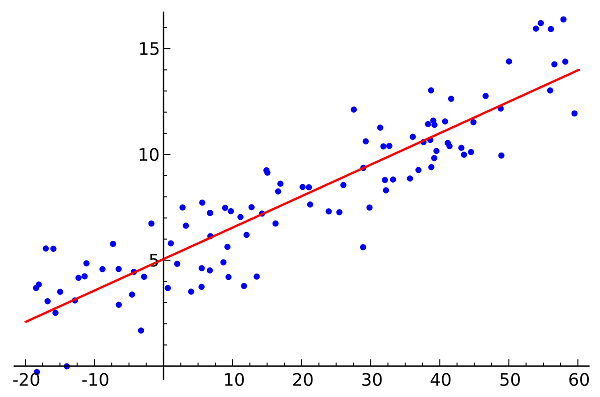
Why we use Regression Analysis?
As referenced over, the regression analysis assesses the connection between at least two factors. How about we comprehend this with a simple model:
Suppose, you need to appraise development in offers of an organization dependent on current monetary conditions. You have the ongoing organization information which shows that the development in deals is around more than multiple times the development in the economy. Utilizing this understanding, we can manipulate future offerings of the organization dependent on current and past data.
There are numerous advantages of utilizing regression analysis. They are as per the following:
1>. It shows the critical connections between the reliant variable and autonomous variable.
2>. It shows the quality of the effect of various free factors on a needy variable.
Regression analysis likewise enables us to analyze the impacts of factors estimated on various scales, for example, the impact of value changes and the quantity of special exercises. These advantages help economic specialists/information examiners/information researchers to dispense with and assess the best arrangement of factors to be utilized for structure prescient models.
What are different types of regression methods do we have?
There are different sorts of regression methods accessible to make expectations. These procedures are for the most part determined by three measurements (number of free factors, kind of ward factors and state of regression line). We'll examine them in detail in the accompanying areas.
For the innovative ones, you can even concoct new regressions, on the off chance that you want to utilize a mix of the parameters above, which individuals haven't utilized previously. Be that as it may, before you begin that, let us comprehend the most normally utilized regressions:
- Linear Regression
- Logistic Regression
- Polynomial Regression
- Stepwise Regression
- Ridge Regression
- Lasso Regression
- Elastic Net Regression
Example of a Simple Linear Regression Model:
Problem Statement :
In this example we have a sample dataset 15 human weights and waist sizes and we are predicting the general trend between them.
Code :
# import the libraries
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn import linear_model
# load dataset
data = pd.read_csv('Book1.csv')
Link to download the dataset :Click here
# checking the correctness of database
data
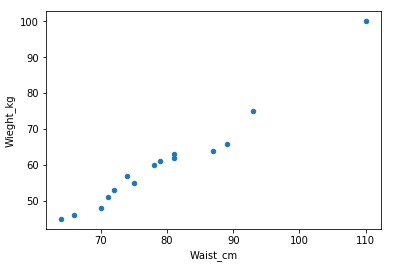
# Plotting a scatter plot on the basis of the given dataset
data.plot(kind='scatter' ,x='Waist_cm' ,y='Wieght_kg')
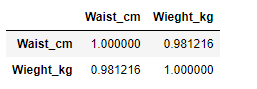
# finding the correlation between the both columns
data.corr()
# converting the both variables in dataframe varibles
Waist = pd.DataFrame(data['Waist_cm'])
Weight = pd.DataFrame(data['Wieght_kg'])
#building the linear model out for this dataset
linear = linear_model.LinearRegression()
model = linear.fit(Waist,Weight)
# finding the coefficient of the graph
model.coef_
model.intercept_
coeff : array([[1.13470708]])
intercept: array([[-29.62009537]])
# predicting the score of model accuracy
model.score(Waist,Weight)
# On the basis of the model we trained predicting the values
Waist_new = [82,94,95]
Waist_new = pd.DataFrame(Waist_new)
Wieght_new = model.predict(Waist_new)
Wieght_new

# converting the predicted values into dataframe and concatinanting the waist and weight values
Wieght_new = pd.DataFrame(Wieght_new)
df = pd.concat([Waist_new,Wieght_new], axis=1 ,keys=['Waist_new','Wieght_predicted'])
# Ploting the visual graph from the data with the regression line
data.plot(kind='scatter' , x= 'Waist_cm' ,y= 'Wieght_kg')
# plotting the regression line
plt.plot(Waist,model.predict(Waist),color='green' , linewidth=2)
# plotting the predicted values
plt.plot(Waist_new,Wieght_new ,color='black', linewidth=4)
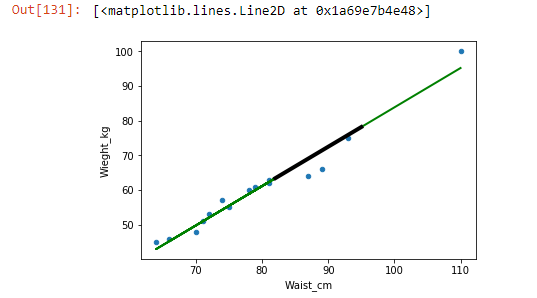
This green line is the best fit line which is unique in each dataset as the difference between datapoints and the line is minimum for each datapoint.
Time Complexity of Regression Models :
If n is the number of training data.W is the number of weights and each resolution of the weight space is set to m meaning will iterate through m meaning that eachweight will iterate through m number of possible values. Then the time complexity of this linear regression is O((m**w)n)
Applications of regression models :
It has various kinds of applications of which some are mostly used in data science I.e:
-
Predictive Analysis: This application is the most prominent one as it is used in business growth and demand analysis. It helps the industries to predict the demand of an item in the market.
-
Operation Efficiency: Regression can also be used to optimize business process.
How to choose the correct regression model?
Life is generally basic when you know just a couple of strategies. One of the preparation establishments I am aware of tells their understudies – if the result is ceaseless – apply straight regression. On the off chance that it is twofold – utilize calculated regression! Be that as it may, Higher the number of choices accessible available to us, increasingly troublesome it progresses toward becoming to pick the correct one. A comparative case occurs with regression models.
Inside different kinds of regression models, it is imperative to pick the most appropriate method depends on the sort of autonomous and ward factors, dimensionality in the information and other fundamental attributes of the information. The following are the key factors that you should practice to choose the correct regression model:
-
Information investigation is an unavoidable piece of structure a prescient model. It ought to be your initial step before choosing the correct model like recognize the relationship and effect of factors .
-
To look at the decency of fit for various models, we can dissect various measurements like the factual essentialness of parameters, R-square, Adjusted r-square, AIC, BIC and mistake term. Another is Mallow's Cup standard. This checks for conceivable inclination in your model, by contrasting the model and all conceivable sub models (or a cautious determination of them).
-
Cross-approval is the most ideal approach to assess models utilized for expectation. Here you separate your informational index into two gatherings (train and approve). A basic mean squared distinction between the watched and anticipated qualities give you a measure for the expected precision.
-
If your informational collection has various bewildering factors, you ought not to pick the programmed model choice strategy since you would prefer not to place these in a model simultaneously.
-
It'll likewise rely upon your goal. A less incredible model might be anything but difficult to actualize when contrasted with an exceptionally measurably huge model.
-
Regression regularization methods (Lasso, Ridge, and Elastic Net) functions admirably in the event of high dimensionality and multicollinearity among the factors in the informational collection.
