Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
Reading time: 30 minutes | Coding time: 10 minutes
In this article, we will explore an algorithm to convert a Binary Search Tree (BST) into a Balanced Binary Search Tree. In a balanced BST, the height of the tree is log N where N is the number of elements in the tree. In the worst case and in an unbalanced BST, the height of the tree can be upto N which makes it same as a linked list. The height depends upon the order of insertion of elements while some other trees like AVL tree has routines to keep their tree balanced which is not present in a normal Binary Search Tree. It is important to keep a BST balanced, as it will give best performance for tasks it is build for like:
- searching elements in O(log N)
The conversion to a Balanced Binary Search Tree takes O(N) time complexity
Example:
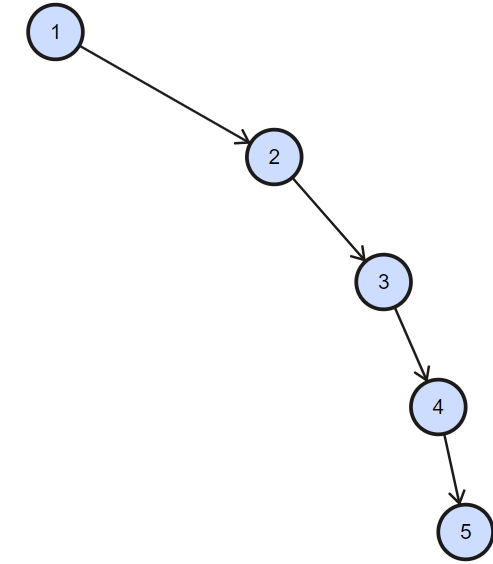
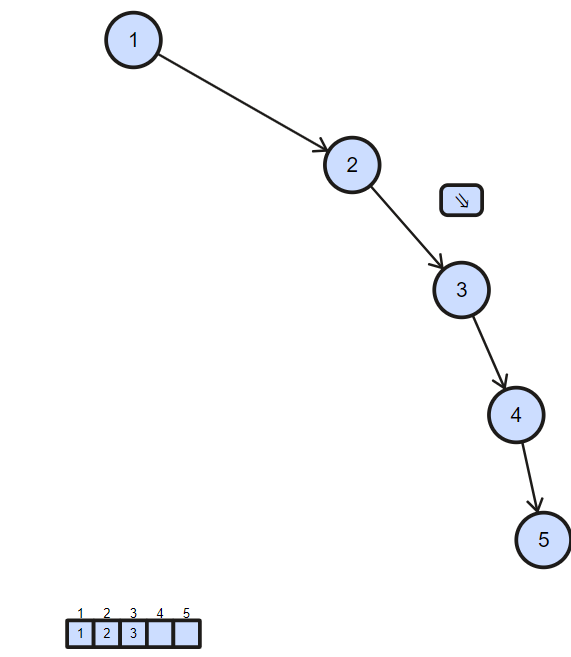
Input of an unbalanced Binary Search Tree:
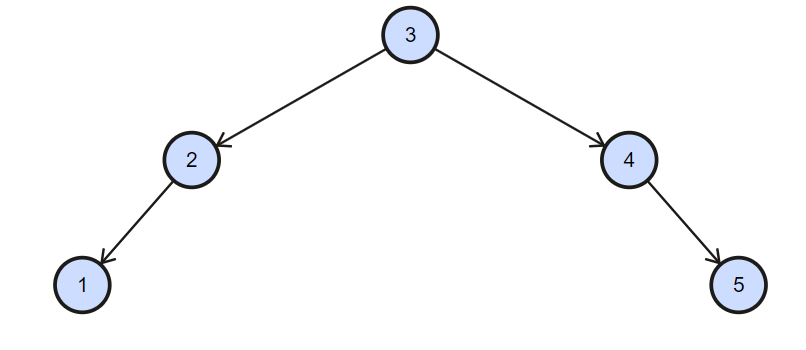
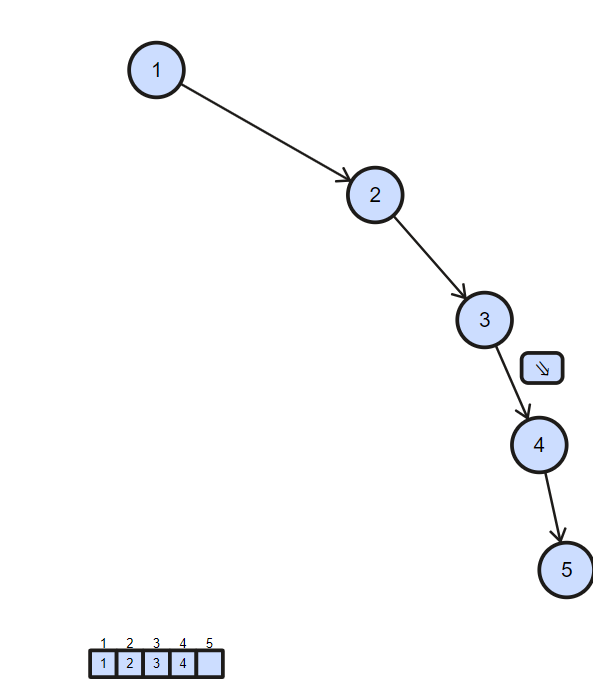
Output of the same tree but as a balanced Binary Search Tree:
As we know the property of binary search tree, inorder traversal of binary search tree gives element in sorted order which are stored in binary search tree.And then we can form the balanced binary search from the sorted array.
Algorithm:
- Traverse given BST in inorder and store result in an array. This step takes O(n) time. Note that this array would be sorted as inorder traversal of BST always produces sorted sequence.
- Get the Middle of the array and make it root.
- Recursively do same for left half and right half.
- Get the middle of left half and make it left child of the root created in step 1.
- Get the middle of right half and make it right child of the root created in step
Implementation
Following is the implementation of the above algorithm.
#include <bits/stdc++.h>
using namespace std;
struct node
{
int key;
struct node *left, *right;
};
// A utility function to create a new BST node
struct node *newNode(int item)
{
struct node *temp = (struct node *)malloc(sizeof(struct node));
temp->key = item;
temp->left = temp->right = NULL;
return temp;
}
/* A utility function to insert a new node with given key in BST */
struct node* insert(struct node* node, int key)
{
/* If the tree is empty, return a new node */
if (node == NULL) return newNode(key);
/* Otherwise, recur down the tree */
if (key < node->key)
node->left = insert(node->left, key);
else if (key > node->key)
node->right = insert(node->right, key);
/* return the (unchanged) node pointer */
return node;
}
/* This function traverse the skewed binary tree and
stores its nodes pointers in vector nodes[] */
void storeBSTNodes(struct node* root, vector<struct node*> &nodes)
{
// Base case
if (root==NULL)
return;
// Store nodes in Inorder (which is sorted
// order for BST)
storeBSTNodes(root->left, nodes);
nodes.push_back(root);
storeBSTNodes(root->right, nodes);
}
/* Recursive function to construct binary tree */
struct node* buildTreeUtil(vector<struct node*> &nodes, int start,
int end)
{
// base case
if (start > end)
return NULL;
/* Get the middle element and make it root */
int mid = (start + end)/2;
struct node *root = nodes[mid];
/* Using index in Inorder traversal, construct
left and right subtress */
root->left = buildTreeUtil(nodes, start, mid-1);
root->right = buildTreeUtil(nodes, mid+1, end);
return root;
}
// This functions converts an unbalanced BST to
// a balanced BST
struct node* buildTree(struct node* root)
{
// Store nodes of given BST in sorted order
vector<struct node*> nodes;
storeBSTNodes(root, nodes);
// Constucts BST from nodes[]
int n = nodes.size();
return buildTreeUtil(nodes, 0, n-1);
}
/* Function to do preorder traversal of tree */
void preOrder(struct node* node)
{
if (node == NULL)
return;
cout<<node->key<<" ";
preOrder(node->left);
preOrder(node->right);
}
// Driver Program to test above functions
int main()
{
struct node *root = NULL;
root = insert(root, 1);
insert(root, 2);
insert(root, 3);
insert(root, 4);
insert(root, 5);
root = buildTree(root);
cout<<"Pre order Traversal of tree"<<endl;
preOrder(root);
return 0;
}
Output:
Pre order Traversal of tree
3 1 2 4 5
Explanation:
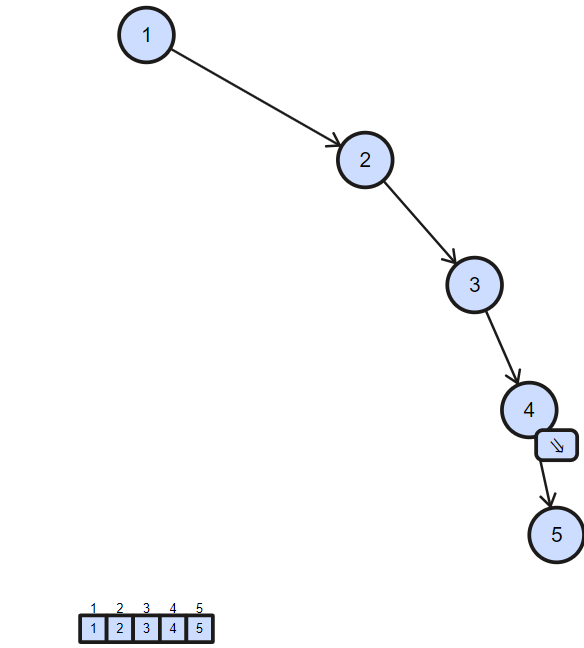
First of all we will do inorder traversal and and store the elements in array.
- First go to the left of the root but it is null therefore go to the root of the tree and store it in an array.
- Then go to the right of the root go to the 2.left check if left child of the 2 is null the store 2 in the array.
- Then go to the right of the 2 and check if the left child of 3 is null the store the 3 in array.
- Then go to the right of 3 and check if the left child of 4 is null then store 5 in the array
- Then go to the right of 4 and check if the left child of 5 is null then store 5 in array. Now check if the right child of 5 is null then return the array.
- Now we will build the balanced binary search tree from the sorted array we obtained through the above process.
- First of all find the the middle of the array i.e. 3 and store it as root of the new tree.
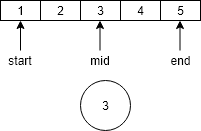
- Then go to the left of the 3 and build the left subtree for that find again the middle of the left sub array of 3 i.e. 2 and store as the left child of 3.
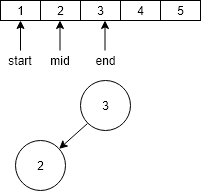
- Then go the left sub array of the 2 and again find the middle of the array and store it as the left child of 2.
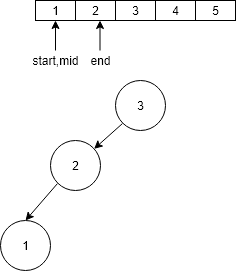
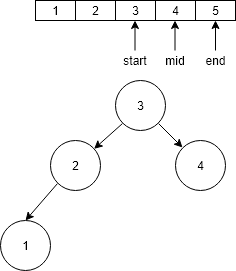
- Now start > end therefore go to root of the tree i.e. 3.
- Now as we have constructed left sub tree in similar way now we will construct right sub tree go to the right sub array and again find the middle of the array i.e. 4 and store it as the right child of 3.
- Now go the right sub array of 4 and again find the middle i.e. 5 and store it as the right child of the 4.
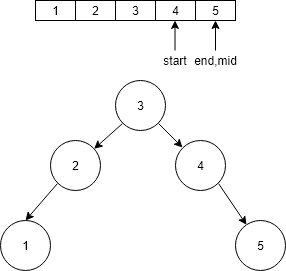
- Now start>end return to root i.e. 3 of the tree.
- Now our Balanced Binary Search Tree is ready.
Time Complexity:
The Inorder Traversal of Binary search tree in O(n) time complexity.
To form Balanced Binary tree from Sorted array , it takes O(n) time to complete.
Following is the recurrence relation for buildTreeUtil().
T(n) = 2T(n/2) + C
T(n) --> Time taken for an array of size n
C --> Constant
(Finding middle of array
linking root to left and right subtrees take constant time)
Therefore, in total this algorithm takes O(N) time to complete.