Find k-th smallest element in Binary Search Tree

Reading time: 30 minutes | Coding time: 10 minutes

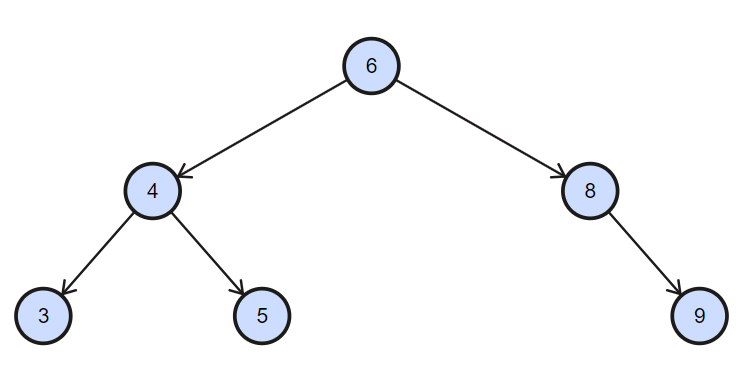
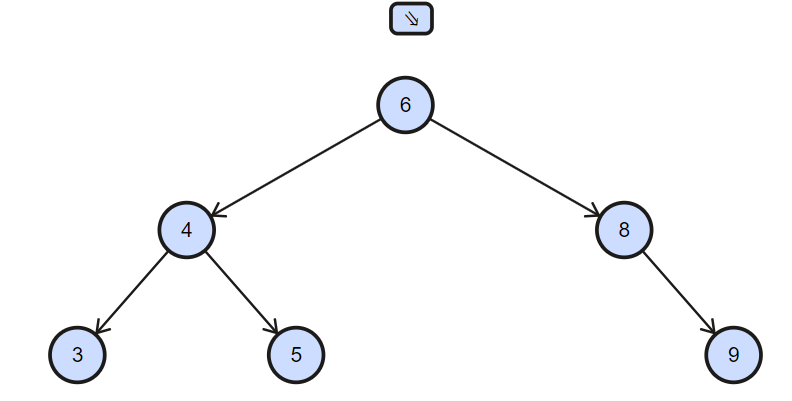
Given root of the tree and k as input, output K th smallest element.
for example in below given tree, for k=3 we will get 5.

The idea simple do inorder traversal store it an array and as we know by the property of the binary search tree inorder traversal gives element of a binary search tree in sorted form.

We will explore two approaches:

• Using inorder traversal (O(N))
• Efficient approach (O(log N))

Algorithm 1: Using inorder traversal O(N)

1. Do the Inorder traversal of the Binary search tree and store the elements in an vector as come in sequence.
2. Then from sorted vector made from above process return the k-th element and it is the output we need.

Below is the Implementation of the above algorithm.

#include <bits/stdc++.h>
using namespace std;
struct node 
{ 
    int key; 
    struct node *left, *right; 
}; 
  
// A utility function to create a new BST node 
struct node *newNode(int item) 
{ 
    struct node *temp =  (struct node *)malloc(sizeof(struct node)); 
    temp->key = item; 
    temp->left = temp->right = NULL; 
    return temp; 
} 
/* A utility function to insert a new node with given key in BST */
struct node* insert(struct node* node, int key) 
{ 
    /* If the tree is empty, return a new node */
    if (node == NULL) return newNode(key); 
  
    /* Otherwise, recur down the tree */
    if (key < node->key) 
        node->left  = insert(node->left, key); 
    else if (key > node->key) 
        node->right = insert(node->right, key);    
  
    /* return the (unchanged) node pointer */
    return node; 
} 
/* This function traverse the skewed binary tree and 
   stores its nodes pointers in vector nodes[] */
void storeBSTNodes(struct node* root, vector<struct node*> &nodes) 
{ 
    // Base case 
    if (root==NULL) 
        return; 
  
    // Store nodes in Inorder (which is sorted 
    // order for BST) 
    storeBSTNodes(root->left, nodes); 
    nodes.push_back(root); 
    storeBSTNodes(root->right, nodes); 
} 
  
/* Recursive function to construct binary tree */

  
// This functions find Kth Minimum Element in BST
int findKthMinimumElement(struct node* root,int k) 
{ 
    // Store nodes of given BST in sorted order 
    vector<struct node*> nodes; 
    storeBSTNodes(root, nodes); 
 
    return nodes[k-1]->key;
} 

// Driver Program to test above functions 
int main() 
{ 
    int k =3;
    struct node *root = NULL; 
    root = insert(root, 6); 
    insert(root, 4); 
    insert(root, 5); 
    insert(root, 3); 
    insert(root, 8); 
    insert(root, 9); 
    cout<<"The "<<k<<" th smallest element in Binary search tree is "<<findKthMinimumElement(root,k);
} 

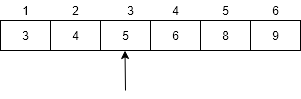
Output:

The 3 th smallest element in Binary search tree is 5

Explanation:

• First of all we go to the left most element of the tree and store it in an vector.
  
  
• Then return back to parent element and store it in an array.
  
  
• Then go to the right of present node and check it left child is present of right child of the present node then store it in a array and store it in vector.
  
  
• Then check the right children if it is not exist then go to parent and then again return to parent of parent because it is visited and store it in vector.
  
  
• Then go to the right child of present node and check if left child does not exist the store the present node in vector.
  
  
• The right child of the present node and check if left child exist then go there otherwise store the present element in the vector.
• Then check it right child exist then go there if not then go tothe root and now all the nodes are visited therefore return to the main function.
  
  
• Now required element is the k th one in the array therefore return it and it is required output.
  

Time Complexity:

Inorder Traversal of Binary search Tree takes O(n) time and fetching the K th element from vector requires O(1) time.
Therefore, all over time complexity of this algorithm is O(n).

Efficient Approach O(log N)

The idea to maintain the the rank of each node. we will count the number of nodes in the left subtree of each node so this will give the rank of the node. It will help us to find the element in o(h) time. see below algorithm for more understanding.
Algorithm:

start:
if K = root.leftElement + 1
   root node is the K th node.
   goto stop
else if K > root.leftElements
   K = K - (root.leftElements + 1)
   root = root.right
   goto start
else
   root = root.left
   goto start

stop:

Implementation of above algorithm in c++

#include <bits/stdc++.h>
using namespace std;
  
typedef struct node node; 
  
/* Binary tree node */
struct node 
{ 
    int data; 
    int lCount; 
  
    node* left; 
    node* right; 
}; 
 
 node *newNode(int item) 
{ 
    
         node *new_node = (node *)malloc( sizeof(node) ); 
  
        /* initialize */
        new_node->data   = item; 
        new_node->lCount = 0; 
        new_node->left   = NULL; 
        new_node->right  = NULL; 
        
        return new_node;
} 
/* Iterative insertion 
   Recursion is least preferred unless we gain something 
*/
node *insert(node *root, int data)
{ 
    node *node_t = newNode(data);
    /* A crawling pointer */
    node *pTraverse = root; 
    node *currentParent = root; 
  
    // Traverse till appropriate node 
    while(pTraverse) 
    { 
        currentParent = pTraverse; 
  
        if( node_t->data < pTraverse->data ) 
        { 
            /* We are branching to left subtree 
               increment node count */
            pTraverse->lCount++; 
            /* left subtree */
            pTraverse = pTraverse->left; 
        } 
        else
        { 
            /* right subtree */
            pTraverse = pTraverse->right; 
        } 
    } 
  
    /* If the tree is empty, make it as root node */
    if( !root ) 
    { 
        root = node_t; 
    } 
    else if( node_t->data < currentParent->data ) 
    { 
        /* Insert on left side */
        currentParent->left = node_t; 
    } 
    else
    { 
        /* Insert on right side */
        currentParent->right = node_t; 
    } 
  
    return root; 
} 
  
int findKthMinimumElement(node *root, int k) 
{ 
    int ret = -1; 
  
    if( root ) 
    { 
        /* A crawling pointer */
        node *pTraverse = root; 
  
        /* Go to k-th smallest */
        while(pTraverse) 
        { 
            if( (pTraverse->lCount + 1) == k ) 
            { 
                ret = pTraverse->data; 
                break; 
            } 
            else if( k > pTraverse->lCount ) 
            { 
                /*  There are less nodes on left subtree 
                    Go to right subtree */
                k = k - (pTraverse->lCount + 1); 
                pTraverse = pTraverse->right; 
            } 
            else
            { 
                /* The node is on left subtree */
                pTraverse = pTraverse->left; 
            } 
        } 
    } 
  
    return ret; 
} 
  
/* Driver program to test above functions */
int main(void) 
{ 
   int k =3;
    node *root = NULL; 
    root = insert(root, 6); 
    root=insert(root, 4); 
    root=insert(root, 5); 
    root=insert(root, 3); 
    root=insert(root, 8); 
    root=insert(root, 9); 
    cout<<"The "<<k<<" th smallest element in Binary search tree is "<<findKthMinimumElement(root,k);
    return 0; 
} 

Explanation:

• Start with the root compare the lcount with k if k is equal to lcount then break if k<lcount then go the left otherwise go right. Subtract lCount+1 from k
  
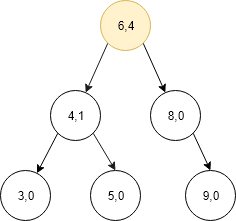
• In our example, k is smaller then lcount therefore we come to the left child now again compare lcount of the current node and k.Subtract lCount + 1 from k
  
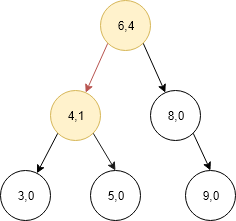
• As we can see than lcount of the current node is less than k therefore we go right child now.
  
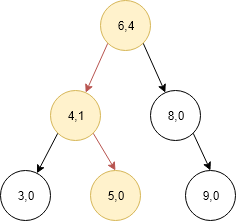
• Now we can see that lcount of current node is equal to k therefore return the value of that node which is our output.