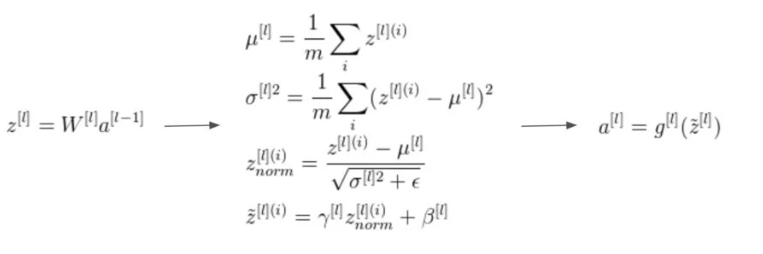Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
Reading time: 30 minutes | Coding time: 15 minutes
Batch normalization or also known as batch norm is a technique used to increase the stability of a neural network. It helps our neural network to work with better speed and provide more efficient results. Batch Normalization was first introduced by two researchers at Google, Sergey loffe and Christian Szegedy in their paper ‘Batch Normalization: Accelerating Deep network training by Reducing Internal Covariate Shift’ in 2015.
Why do we need Batch Normalization?
Consider the following example, let us say the we have one parameter (say age) which will be in the range 1 to 100. Now if we have another parameter like salary which will be in the range of 10000 to 1000000, and we are supposed to calculate some output based on these parameters then some problems will be introduced in our network due to such difference in scaling. So, what we can do is normalize these parameters say in the range of 0 to 1 and this will help us speed up the learning process.
Now initially this was proposed for the input layer, but it turns out that applying it to the hidden layers was quite helpful. Using batch normalization, the shift in the hidden unit values (i.e. covariance shift) is reduced to a great extent. One example of covariance shift can be this, let us say we prepared and trained a model that tells us whether there is a dog in the input image. If there is a dog, then the output is 1 else 0. Now if the training set contains only the images of black dogs and for prediction, we gave input as the image of a colored dog, then our model would not perform with good efficiency. This is what covariance shift basically means.
Another popular reason for using batch normalization is dealing with vanishing/exploding gradient problem. Let us say we have a certain neural network, now the forward propagation multiplicatively depends on each weight and the activation function. In backpropagation the partial derivatives keep getting multiplied by weights and activation function derivatives. Unless the values are exactly 1, the partial derivatives will either continuously increase(explode) or decrease(vanish). Due to this our networks efficiency goes on decreasing.
How does it work?
Batch normalization is applied to layers that you choose to apply it to. The first thing that happens in batch norm is normalize the output from the previous activation function. This done as follows:
Z = (X-M) / S
So, here from the output from the activation layer(X), batch mean(M) is subtracted and then the whole thing is divided by the batch standard deviation(S).
After that, batch norm multiplies the normalized output with some arbitrary parameter (say F).
Z = Z * F
Finally batch norms adds another arbitrary parameter to this above product (say B).
Z = Z * F + B
All these parameters like M, S, F and B are all trainable i.e. these will also be optimized during the training process.
The following image shows this process:
In the above example, the first two equations represent the functioning of simple nodes of a Neural network. Then in the third line, the mean subtraction and division by standard deviation takes place. Finally in the last line, the arbitrary parameters gamma and beta are introduced.
Now, the normalization to activations can be done in two formats:
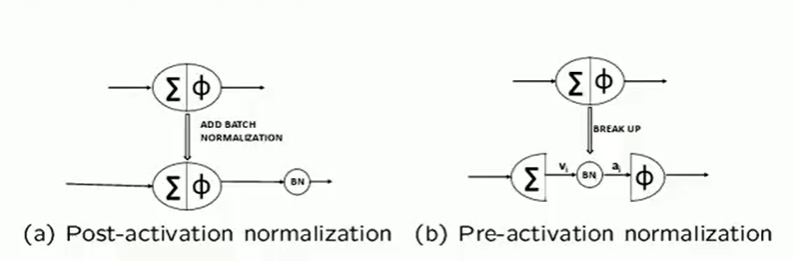
- Post activation normalization
- Pre-activation normalization
In pre-activation normalization, the BN layer is added before the activation function is applied and in post activation normalization, the BN layer is added after the activation layer computations are done.
When the concept of batch norm was introduced, it was proposed that normalization before activtion will be very beneficial. But it was found that applying batch norm after activation yields better results.
Implementation example
The basic algorithm that can be used in batch norm implementation can be given as follows:

The code for the above algorithm can be written as follows:
def batchnorm(x, gamma, beta, eps=1e-5):
N, D = x.shape
sample_mean = x.mean(axis=0)
sample_var = x.var(axis=0)
std = np.sqrt(sample_var + eps)
x_centered = x - sample_mean
x_norm = x_centered / std
out = gamma * x_norm + beta
cache = (x_norm, x_centered, std, gamma)
return out, cache
In the above algorithm, first mean and variance are computed followed by standard deviation. After that the main steps of batchnorm are done i.e. mean is subtracted from x and then the subtracted value is divided by standard deviation. Also, parameters beta and gamma are introduced. Alpha and beta are both trainable parameters.
Now we will see a simple implementation example of the batch normalization using the keras modules in python.
Here first we will consider a simple neural network with two layers and certain configurations. Consider the python code below:
from keras.models import Sequential
from keras.layers import Dense, Activation, BatchNormalization
model = Sequential([
Dense(16, input_shape=(1,5), activation='relu'),
Dense(32, activation-'relu'),
BatchNormalization(axis=1),
Dense(2, activation='softmax')
])
From the above code we see that there is one input layer, one hidden layer and a final output layer in our network. The input layers consist of 16 units. The hidden layers consist of 32 units, both input and hidden layers have Rectified linear unit i.e. Relu as the activation function. Finally the output layers has two output categories using the softmax function.
Now we see that the batch normalization in keras is initialized the way shown above. It is introduced after the layer (here specified after the hidden layer) whose output we want to normalize. For this to work, we are required to import the BatchNormalization from keras.
So this is how most basic implementation of Batch Normalization is done.