Boyer Moore String Search Algorithm

Boyer Moore string search algorithm is an efficient string searching algorithm which was developed by Robert S. Boyer and J Strother Moore in 1977.

Given a string S of length n and a pattern P of length m , you have to find all occurences of pattern P in string S provided n > m.

Naive Approach

In naive or brute approach, we check occurence of pattern in string at every poisition i from 1 to n of the string. This approach has time complexity: O(|P| * |S|) or O(m * n). As in the worst case we may check the whole pattern at every possible index of the string. Pseudocode is given below:-

1. result = []
2. for i =: 1 to n - m + 1, do:
3.     for j =: 1 to m, do:
4.         if S[i+j-1] != P[j] : break
5.         else if j == m: result.append(i)

Efficient Algorithm

The main idea behind the efficient approach is that in brute force we have to check every position despite knowing that some positions will never match. So, if we somehow find a way to skip some of the positions that give no useful info we can significantly lower our time used. Before we proceed further we need to know about Bad Character Heuristic and Strong Suffix Heuristic.
In boyer moore there are two ways of skipping positions:-
1. Bad Character Heuristic.
2. Good Suffix Heuristic.

Bad Character Heuristic

After alignment of pattern along text we start matching pattern and text character by character from right end of pattern until we get first unmatched character and then we try to shift pattern to right side in such a way that this unmatched character get matched with shifted alignment of pattern. Note that pattern can be aligned such that either mismatch become a match or pattern move past the mismatch character.Given below is an example to demonstrate:

Precomputation for bad character heuristic, we just need to store index of last occurence of each character in pattern in array.For above example badCharacterArray is like one given below: A well commented code is given below for precomputation of both heuristic.

Good Suffix Heuristic

After alignment of pattern along text we start matching pattern and text character by character from right end of pattern untill we get first unmatched character and then we try to align pattern to right side in such a way that the matched substring or its suffix get matched again.There can be three cases:

1. Another occurence of matched substring found in pattern. Given below an example, The substring "ab" is matched. The pattern can be shifted until the next occurence of ab in the pattern is aligned to the text symbols ab, i.e. to position 2.
2. A prefix of pattern get matched with suffix of matched substring. In the following situation the suffix "bab" has matched. There is no other occurence of "bab" in the pattern. But in this case the pattern cannot be shifted to position 5 as before, but only to position 3, since a prefix of the pattern (ab) matches the end of bab.
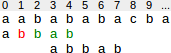
3. Pattern moves past matched substring. In the following situation the suffix ab has matched. There is no other occurence of ab in the pattern.Therefore, the pattern can be shifted behind ab, i.e. to position 5.
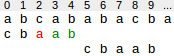
In precomputation of shift according to good suffix heuristic it is required to understand concept of border. I would suggest you to read my blog on KMP Here.In KMP we already used border to find shift but there we find border for all prefixes and here we are going to find border of all suffixes of pattern.Note that logic behind algorithm of finding border for each prefix is same as written in KMP but here we start our calculation from right end. With the help of border we compute shift array, whose value at each index represent the amount of alignments we can safely skips if mismatch occur at corresponding index.
Lets consider a pattern ANPANMAN, now its shift array will look like image given below:

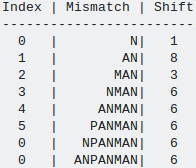
1. In first row, mismatch occur at first comparision i.eN and as here there is no matched suffix so we can get maximum shift of 1.
   
2. In second row, mismatch occur in second comparision i.e A and now we try to find another N which is not preceded by A and as there no such substring "*N"(here * star can be any character except A) in pattern so we shift pattern by size of pattern.i.e 8.(Case 3)
   
   3.In third row, substring "AN" is matched and mismatch is due to character "M", so we try to find substring of form "*AN"(where * can be any character except M) and we found substring "PAN" at index 2 of pattern this alignment can be possible shifting pattern by 3 positions.(Case 1)
   
   In similar way remaining values of remaining indices will be calculated.

Complexity

Time Complexity for precomputation: O(m + size of alphabet)

Time Complexity for searching: O(n)

Space Complexity: O(m + size of alphabet)

Implementation

#include <bits/stdc++.h>
using namespace std;
#define CHARSETSIZE 26 
// I am considering that only A-Z capital letters are allowed in TEXT and PATTERN  


///PreComputation for Bad Character Heuristic
vector<int> badCharacterPreComputation(string pattern)
{
	vector<int> badCharacterArray( CHARSETSIZE, -1);
	for(int i=0; i < pattern.size(); i++)
	{
		//We are storing the last occurence of each latters
		badCharacterArray[pattern[i]-65]=i;   
	}
	return badCharacterArray;
}
//////////

///PreComputation of shifts for Good Suffix Heristic
vector<int> goodSuffixHeuristicPreComputation(string pattern)
{
	int m=pattern.size(), i=m, j=m+1;

	// Initialize all shift with zero
	vector<int> borderPos(m+1), shifts(m+1,0); 
	
	borderPos[i]= j;
	// Loop given below is used to find border for each index
	while(i> 0)  
	{
		/*
			if character at position i-1 is not equal to 
          character at j-1, then continue searching to right 
          of the pattern for border. 
			*/
		while( j<=m && pattern[i-1]!= pattern[j-1])
		{
			/*
			The preceding character of matched string is diffent than
			mismatching character. 
			*/
			if(shifts[j]==0)
				shifts[j] = j-i;
			
			// update the position of next border
			j = borderPos[j]; 
		}
		/*As pattern[i-1] is equal to pattern[j-1], position of border 
		for prefix starting from  i-1 is j-1*/
		i--;
		j--;
		borderPos[i] = j;
	}
	/* untill now we calculated shift according to case1 i.e when full matched
	substring with different preceding charater exists in pattern*/
	
	/* now we will fill those shifts generated beacause of case 2 i.e some suffix
	of matched string is found as prefix of pattern
	*/
	j= borderPos[0];
	for(i=0; i<=m; i++)
	{
		if(shifts[i] == 0)
			shifts[i] = j;
		if(i == j)
			j = borderPos[j];
	}
	return shifts;
}	
////////

vector<int> boyerMooreSearch(string text, string pattern)
{
	int i=0, j, m=pattern.size();
    int badShift,goodShift;
    //preprocessing
	vector<int> badCharacterArray= badCharacterPreComputation(pattern);
	vector<int> shifts= goodSuffixHeuristicPreComputation(pattern);
	vector<int> results;
	while(i <= text.size()-m)
	{
		j=m-1;
		while(j>=0 && pattern[j]==text[i+j])
			j--;

		if(j<0)
		{
			results.push_back(i);
			badShift= (i+m < text.size())? m - badCharacterArray[text[i+m]]: 1;
			goodShift = shifts[0];
			i+=max(badShift,goodShift); //We take max shift from both heuristic
		}
		else
		{
			badShift= max(1, j - badCharacterArray[text[i+j]]);
			goodShift = shifts[j+1];
			i+=max(badShift,goodShift); //We take max shift from both heuristic
		}

	}
	return results;
}

int main()
{
	string pattern, text;
	cin>>text>>pattern;
	vector<int> result= boyerMooreSearch(text, pattern);
	if(result.size()==0)
		cout<<"Pattern is not found in given text!!\n";
	else
	{
		cout<<"Pattern is found at indices: ";
		for(int i=0; i< result.size(); i++)
			cout<< result[i] <<" ";
	}
	return 0;
}

Application

1. Boyer-Moore algorithm is extremely fast when large number of alphabets are involved in pattern. (relative to the length of the pattern)
2. Combination of Aho-Corasick Algorithm and Boyer Moore Algorithm is used in Network Intrusion detection systems to find malicious patterns in requests from intruder. To know more about it refer here .