We will develop a Calculator Console Application in Java Programming Language that uses the previous result in the next calculation and includes Shunting Yard Algorithm.

We'll discuss:

• Introduction
• Features
• Understanding the Shunting Yard Algorithm
• How to Implement the Shunting Yard Algorithm?
• Calculator Logic in Java

  • main() method
  • evaluate() method
  • hasPrecedence() method
  • applyOp() method

• Working of evaluate() method
• Need of hasPrecedence() method
• Further Improvements
• Conclusion

Introduction

In today’s fast-paced world, a calculator is a handy tool to have for performing quick calculations on the go. In this article, we will be discussing how to create a simple calculator console application in Java. We will go through the process of building the application step by step, including the implementation of basic mathematical operations and handling of user inputs.

By the end of this article at OpenGenus, you will have a solid understanding of how to create your own calculator application in Java and will have the knowledge to enhance it with additional features. So, let's get started.

Features

The features that we plan to implement in our calculator include:

• This is a Java console application that can perform basic arithmetic operations such as addition, subtraction, multiplication, and division.
• The program can handle user input in the form of infix notation and will convert it to postfix notation using Shunting Yard algorithm.
• The calculator can handle parentheses and floating-point numbers in the expressions.
• The program has a feature that stores the previous result, which can be used as an operand in the next expression.
• The program can be exited by entering “q” and will throw an error if the user attempts to divide by zero.

Understanding the Shunting Yard Algorithm

The Shunting Yard algorithm is a method used to convert a mathematical expression written in infix notation (e.g., "3 + 4 * 2 / (1 - 5)") to postfix notation (e.g., "3 4 2 * 1 5 - / +").

This algorithm was invented by Edsger Dijkstra, and it uses two stacks, one for operators and one for operands, to change the order of the operators and operands in the expression. By converting the expression to postfix notation, it becomes easier to evaluate the expression using a simple algorithm.

The Shunting Yard algorithm can be used to create a calculator or a parser for a programming language.

How to Implement the Shunting Yard Algorithm?

To implement the Shunting Yard Algorithm in a calculator program written in java, we first need to create two stacks - one for operands and one for operators.

We then take the input expression (in infix notation) and process it character by character. For each character, we check whether it is an operand or an operator. If it is an operand, we add it to the operand stack. If it is an operator, we check its precedence and compare it to the operators already on the operator stack. If the new operator has higher precedence, we add it to the operator stack. If the new operator has lower precedence, we pop operators off the operator stack and add them to the output queue until the operator on the top of the stack has lower precedence than the new operator.

Once we have processed all characters in the input expression, we pop any remaining operators off the operator stack and add them to the output queue. The output queue now contains the expression in postfix notation, which we can then evaluate using a simple stack-based process.

Calculator Logic in Java

The logic part of the calculator can be seen here:

main()

import java.util.*;

public class calculator {
    private static double prevResult = 0;

    private static double evaluate(String input) {
        // code is written below
    }

    private static boolean hasPrecedence(char op1, char op2) {
        // code is written below
    }
    
    private static double applyOp(char op, double b, double a) {
        // code is written below
    }

    /* main method is the entry point of the program.
    It prompts the user to enter an expression and uses the evaluate method to evaluate it.
    If the user enters "q", the program will exit.
    The program also has a prevResult variable that keeps track of the previous result, 
    which can be used as an operand in the next expression. 
    If the user enters an expression that starts with an operator, 
    it is assumed that the user wants to use the previous result as the first operand and 
    the input string is modified accordingly before being passed to the evaluate method
    */ 
    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        while (true) {
            System.out.println("Enter expression (or 'q' to exit): ");
            String input = sc.nextLine();
            if (input.equalsIgnoreCase("q")) {
                break;
            }
            if (input.charAt(0) == '+' || input.charAt(0) == '-' || input.charAt(0) == '*' || input.charAt(0) == '/') {
                input = prevResult + input;
            }
            prevResult = evaluate(input);
            System.out.println("Result: " + prevResult);
        }
        sc.close();
    }
}

The main method is the entry point of the program. It prompts the user to enter an expression and uses the evaluate method to evaluate it. If the user enters "quit", the program will exit.

The program also has a prevResult variable that keeps track of the previous result, which can be used as an operand in the next expression. If the user enters an expression that starts with an operator, it is assumed that the user wants to use the previous result as the first operand and the input string is modified accordingly before being passed to the evaluate method.

evaluate() method

private static double evaluate(String input) {
    /*
     * evaluate method takes a string input and evaluates it as a mathematical
     * expression
     * using two stacks, one for operands and one for operators.
     * It uses the Shunting Yard algorithm to convert the input string from infix
     * notation to postfix notation
     * and then evaluates it.
     */
    double result = 0;
    char[] inputArr = input.toCharArray();
    // Create two stacks, one for operands and one for operators
    Stack < Double > operands = new Stack < > ();
    Stack < Character > operators = new Stack < > ();
    // Iterate through the input array
    for (int i = 0; i < inputArr.length; i++) {
        // If the current character is a digit, add it to the operands stack, otherwise
        // add it to the operators stack
        if (inputArr[i] == ' ') {
            continue;
        }
        if (inputArr[i] >= '0' && inputArr[i] <= '9') {
            // if the character is a digit, push it onto the operands stack
            StringBuilder sb = new StringBuilder();
            while (i < inputArr.length && (inputArr[i] >= '0' && inputArr[i] <= '9' || inputArr[i] == '.')) {
                sb.append(inputArr[i++]);
            }
            operands.push(Double.parseDouble(sb.toString()));
            i--;
        } else if (inputArr[i] == '(') {
            // if the character is an open parenthesis, push it onto the operators stack
            operators.push(inputArr[i]);
        } else if (inputArr[i] == ')') {
            // if the character is a close parenthesis, pop operators and operands from
            // their stacks and apply them until an open parenthesis is found
            while (operators.peek() != '(') {
                operands.push(applyOp(operators.pop(), operands.pop(), operands.pop()));
            }
            operators.pop();
        } else if (inputArr[i] == '+' || inputArr[i] == '-' || inputArr[i] == '*' || inputArr[i] == '/') {
            // if the character is an operator, pop operators and operands from their stacks
            // and apply them until the current operator has higher precedence
            while (!operators.empty() && hasPrecedence(inputArr[i], operators.peek())) {
                operands.push(applyOp(operators.pop(), operands.pop(), operands.pop()));
            }
            operators.push(inputArr[i]);
        }
    }
    // pop remaining operators and operands from their stacks and apply them
    while (!operators.empty()) {
        operands.push(applyOp(operators.pop(), operands.pop(), operands.pop()));
    }
    result = operands.pop();
    return result;
}

The evaluate method takes a string input and evaluates it as a mathematical expression using two stacks, one for operands and one for operators. It uses the Shunting Yard algorithm to convert the input string from infix notation to postfix notation and then evaluates it.

hasPrecedence() method

private static boolean hasPrecedence(char op1, char op2) {
/*
hasPrecedence method checks the precedence of the operators.
It returns true if the operator passed as the first argument has higher or
equal precedence than the operator passed as the second argument.
*/
    if (op2 == '(' || op2 == ')') {
        return false;
    }
    if ((op1 == '*' || op1 == '/') && (op2 == '+' || op2 == '-')) {
        return false;
    } else {
        return true;
    }
}

The hasPrecedence method is used to check the precedence of the operators. It returns true if the operator passed as the first argument has higher or equal precedence than the operator passed as the second argument.

applyOp() method

private static double applyOp(char op, double b, double a) {
    /* applyOp method applies the operator passed as the first argument 
    to the operands passed as the second and third arguments. 
    It returns the result of the operation.
     */
    switch (op) {
        case '+':
            return a + b;
        case '-':
            return a - b;
        case '*':
            return a * b;
        case '/':
            if (b == 0) {
                throw new UnsupportedOperationException("Cannot divide by zero");
            }
            return a / b;
    }
    return 0;
}

The applyOp method applies the operator passed as the first argument to the operands passed as the second and third arguments. It returns the result of the operation.

Look at the result,

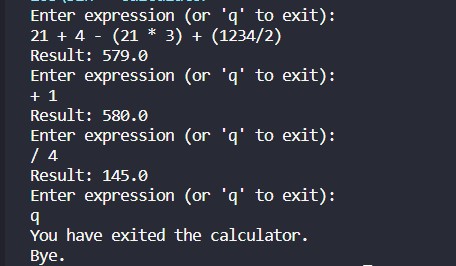
Working of evaluate() method

The evaluate() method is a static method that takes a string input and evaluates it as a mathematical expression. It uses two stacks, one for operands (numbers) and one for operators (e.g., +, -, *, /). The method uses the Shunting Yard algorithm to convert the input string from infix notation (e.g., 2 + 3) to postfix notation (e.g., 2 3 +) and then evaluates it.

The method starts by initializing a variable result to 0 and creating a character array from the input string. It then creates two stacks, one for operands and one for operators, using the Stack class.

The method iterates through the input array and for each character, it checks its type:

• If the character is a space, it is ignored.
• If the character is a digit, it is added to the operands stack as a double.
• If the character is an open parenthesis, it is added to the operators stack.
• If the character is a close parenthesis, the method pops operators and operands from their stacks and applies them until an open parenthesis is found.
• If the character is an operator (+, -, *, /), the method pops operators and operands from their stacks and applies them until the current operator has higher precedence.

After the iteration, the method pops any remaining operators and operands from their stacks and applies them. The final result is stored in the result variable and returned.

For example, if the input string is "2+3*4", the evaluation of the method would be as follows:

• The first character is a digit '2' , it is pushed onto the operands stack.
• The next character is operator '+' , it is pushed onto the operator stack.
• The next character is digit '3', it is pushed onto the operands stack.
• The next character is operator '*', it is pushed onto the operator stack.
• The next character is digit '4', it is pushed onto the operands stack.
• At this point all the characters of the input are processed. Now the remaining operators and operands are popped from their stacks and applied.
• The operator * is applied to operands 4 and 3, which results in 12. This value is pushed onto the operands stack.
• The operator + is applied to operands 12 and 2, which results in 14. This is the final result returned by the method.

Need of hasPrecedence() method

The hasPrecedence method is used to determine the order of operations when evaluating a mathematical expression. It takes two characters as input, the current operator being read from the input string and the operator at the top of the operators stack.

In the example "2 + 3 * 4", hasPrecedence would be called when the operator '*' (multiplication) is being read from the input string and the operator '+' (addition) is currently at the top of the operators stack.

The hasPrecedence method compares the precedence of the two operators, '' and '+', using an if-else statement. In this case, '' has higher precedence than '+', so the method would return true, indicating that the multiplication should be performed before the addition.

This is important because it ensures that the expressions are evaluated correctly according to the order of operations (BODMAS). Without it, the expression "2 + 3 * 4" would be evaluated as (2 + 3) * 4 = 5 * 4 = 20, instead of the correct answer 2 + (3 * 4) = 2 + 12 = 14.

Further Improvements

While the calculator is functional, there are several areas for improvement. Some of the improvements that can be made include:

• Adding support for more advanced mathematical functions such as trigonometric functions, logarithmic functions, etc.
• Implementing error handling to handle invalid expressions or inputs.
• Adding a graphical user interface to make the calculator more user-friendly.
• Implementing support for variables and assignment statements.

Conclusion

In conclusion, we have seen how to create a basic calculator console application in Java using the Shunting Yard algorithm. The calculator is able to evaluate mathematical expressions in infix notation and convert them to postfix notation before evaluating the final result. We have also seen how the program uses two stacks, one for operands and one for operators, to evaluate the expressions.

For the full code, you can visit the link.