This article explains 1-Dimensional Elementary Cellular Automaton, and its applications, and mathematical explanation of concept behind with code in python.

Introduction

Nature has inspired many fields of study, even in computer science. Genetic Algorithms, Machine Learning etc. Another such field, less known but highly impactful is Cellular Automaton.

Aim and Pre-Requisites

This article is a beginner's level introduction to Cellular Automaton with mathematical and coding support. Pre-requisites for reading this article are the motivation to explore a new domain of study, and love of Nature and Computers.

These images explain how Cellular Automaton is not a concept created by Computer Scientists, but exists in nature. Look how patterns similar to Wolfram's Rule 30 of Cellular Automaton (below) is generated in the Textile Cone Shell (above).

What is Cellular Automaton

Cellular Automaton is an evolutionary algorithm, where certain Cell (smallest individual agent of the system) evolves/changes state, based on various rules of evolution. This agent can have multiple states, but exists in a single state at a given time/generation.

If the rules of evolution of a cell's state is based on the state of its neighbors, it is called an Elementary Cellular Automaton.

To simplify things, let us first describe a few things :

1. CELL
   A cell is an individual data block, which can be in multiple states. These states can be Colors, Numbers, Boolean (True/False) etc.

2. GENERATION
   A set of Cells make up a generation. This generation evolves over time, i.e. some rules are applied on the cells so that its state changes. After each iteration of the application of rules, the Generation evolves to the next Generation.

Evolve(Generation_i,Rules) = Generation_i+1

3. SYSTEM
   A set of generations, form a System.

1-D Cellular Automaton

Let us consider a 1-D system, i.e. each generation is an array of Cells.
For simplicity, let us take the cell to be either in state Yes(1) or No(0).

Now let us see evolution of a particular cell, C_i

For a particular Generation, let
{C_i-1,C_i,C_i+1} = {1,1,0}

Now, we can assign a rule, for example, if {1,1,0} state is found for C_i and its neighbors, the next Generation of C_i will be 1.

This can be written as a MAPPING,

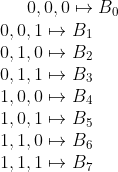
(Note that B₀, B₁...B_m are 0, 1,...m ^th bits (1 or 0) of the m bit binary number n which is written as Rule n or R_n )

Note that this forms a rule, which can be abbreviated as an 8 bit binary number, where its i^th bit represents the value B_i

Now we can abbreviate rule, from a set of 3x1 mapping to an 8 bit binary number, from 0 to 255.

Let us denote the rules as R₀,R₁,R₂...R₂₅₅ for this article.

Let the Array for t^th generation be A_t. Now, one Dimensional cellular automaton can be viewed as an array (or vector) transformation :

Transform(A_t,R_n) = A_t+1
And, the entire system becomes, a 2-D matrix of m generations, each with n cells :

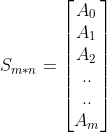
Code for the following transformation in python is

def cell_transform(a,b,c,R): # returns output of {C_(i-1),C_(i),C_(i+1)} by rule R
    n = (a<<2) + (b<<1) + c
    return (R >> n) & 1


def transform(A,R): # R is a number between 0 and 255
    B = []
    for i in range(len(A)):
        B.append(cell_transform(A[i-1],A[i],A[(i+1)%len(A)]))
    return B # next generation

Now, to generate a system, as a Matrix, which contains multiple generations,

# Initial State is A0 and rule is R, and the system consists of m generations
def generate_system(A0,R,m): 
    S = []
    for i in range(m):
        S.append(A0)
        A0 = transform(A0,R)
    return S

Applications of 1-Dimensional elementary cellular automaton

1. Fractals Generation
Interestingly, the Sierpinski Triangle is a result of the result of 1-D Elementary Cellular Automaton. It is a result of Rule 90.
Visualization, is 1 for color, and 0 for whitespace, in a 2-D matrix.

Following are some visualizations and their rules mentioned

RULE 90 - Sierpiński triangle

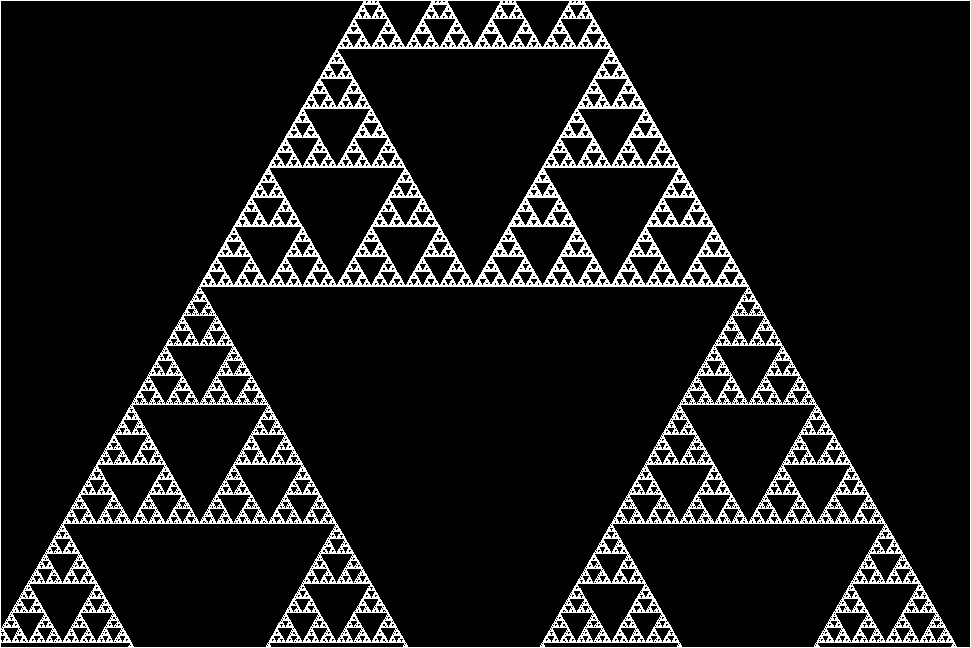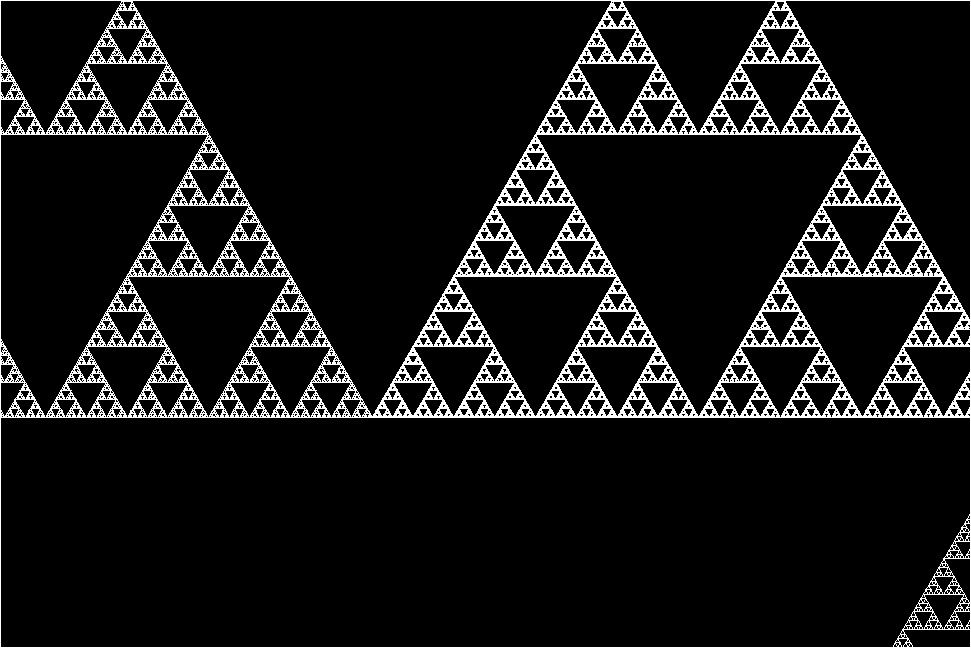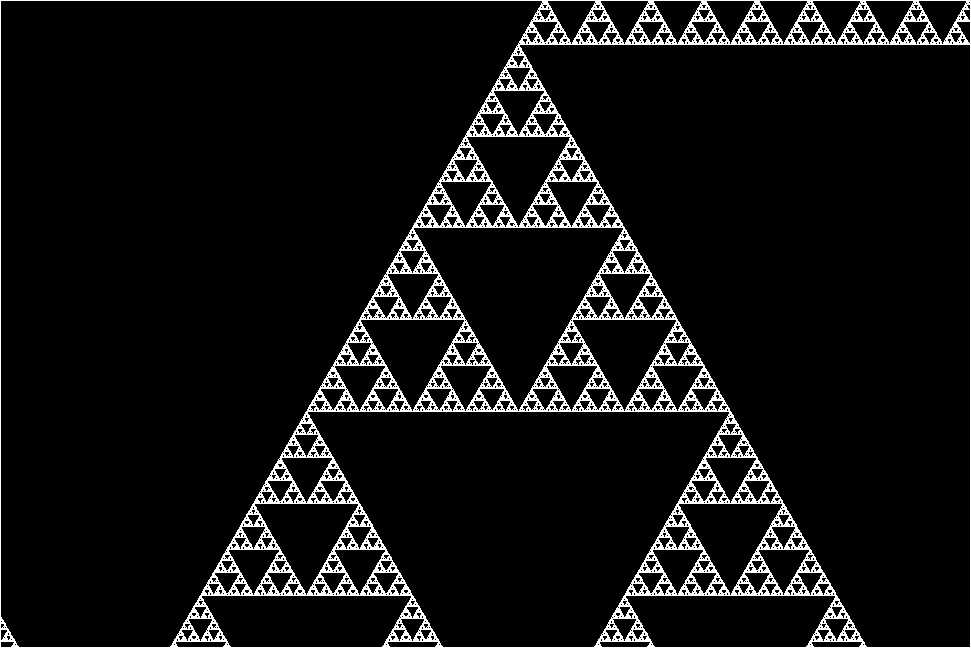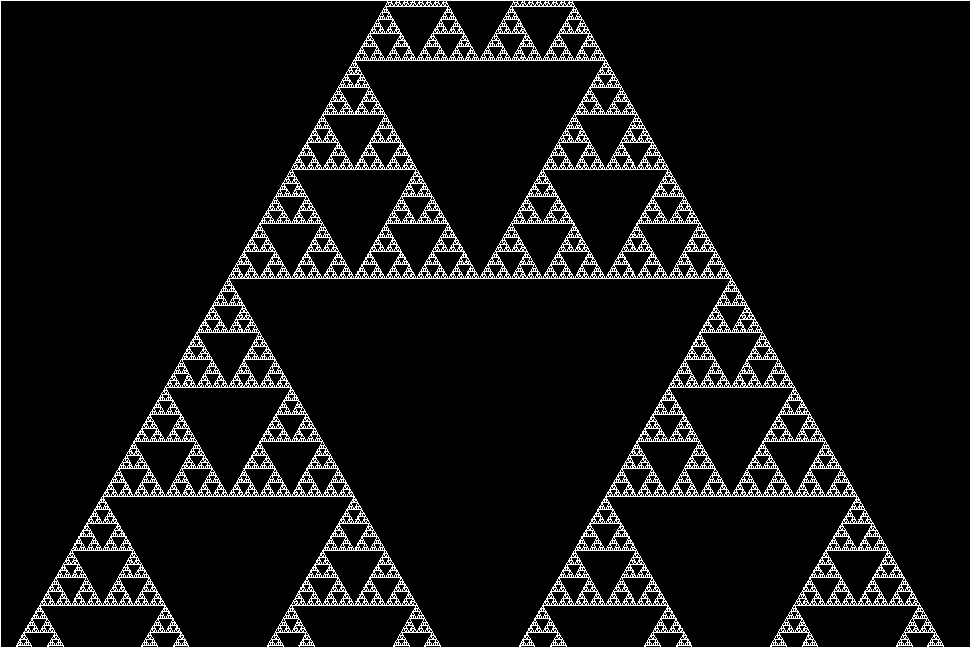
RULE 30 Wolfram's Rule 30

2. Cryptography
Cellular Automaton is also Applied in Cryptography. The Rule 30 Can be used as a pseudo-random number generator.
I have worked on the cryptography application of the topic, and the code, theory and analysis of the same can be found here.

Notice now the wolfram's rule 30 image above can be random if initial conditions are changed. Using this, if we use a seed value for the initial conditions of Wolfram's Rule 30, we can get a Pseudo Random Number Generator, which can be used for Encryption. This is the basic idea of the algorithm for encryption provided in the github repository here.

3. Error Correction Coding
Cellular Automation is applied in error correction and detection codes. The advantage over conventional method is faster decoding time with Cell Automation.
D. Roy Chowdhury, S. Basu, I. Sen Gupta, and P. Pal Chaudhuri have published this paper discussing one such decoder, a single bit error correction, double bit error detection (SEC-DED) scheme.

4. Computer Processors
Multiple 1-D and 2-D Cellular Automaton systems have been proven Turing complete. This implies cellular Automaton systems, can be built as a processor.
There has been no existing implementations, but it can be argued, that taking quantum states of individual particles as CA States, or mimicing inter-cellular interactions by charge transfer, magnetism, vibration etc., nano-processors, or even quantum processors can be a reality.

5. Compression, Simulation, Graphics and Music Generation
This is another interesting application of cellular automaton. It is able to simulate simple multi-agent independent systems, dynamic models like fluid flows etc. Cell Automation is used in image and Data compression also. Olu Lafe has written an excellent paper in this domain (link). It is also used in multimedia generation. Below is a video of generating piano music using 1-D cellular automaton system.

Conclusion

In this article, we learnt about Cellular Automaton on an elementary level. This article's intention was to get us started towards cellular automaton, and try out some cool applications too maybe!

The next level of this is the 2-D cellular transform, and then 3-D cellular transform and Cellular Automaton Transform (CAT). If you found this interesting, then do explore the 2-D variant, and there will you find the Game of Life (repo providing nice visualization, moderate explaination and code in javascript for the Conway's Game of Life),a zero player game, which has a lot to offer.