
Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
In this article, we examine the relationship between Farideh Firoozbakht's famous conjecture about prime numbers, which states that the sequence  where
where 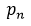 is the nth prime number, is strictly decreasing, and the prime gap function
is the nth prime number, is strictly decreasing, and the prime gap function 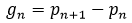 which is the difference between the nth and (n + 1)th prime numbers. Furthermore, Firoozbakht's conjecture is linked to upper limits for the prime gap function in terms of n. Asymptotic outcomes for both the conjecture and the function help us understand the interrelationships.
which is the difference between the nth and (n + 1)th prime numbers. Furthermore, Firoozbakht's conjecture is linked to upper limits for the prime gap function in terms of n. Asymptotic outcomes for both the conjecture and the function help us understand the interrelationships.
Farideh Firoozbakht's initial conjecture in 1982 was that the sequence 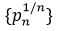 is strictly decreasing, i.e.,
is strictly decreasing, i.e.,
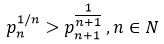
and the first few values of 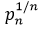 are shown below:
are shown below:

and the speculation has been confirmed for all primes less than 4x(10)^18.
Related forms of Firoozbakht’s conjecture
Following are some alternative formulations of the hypothesis. Here n∈N.
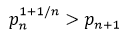 (1),
(1),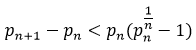 (2),
(2),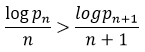 (3),
(3),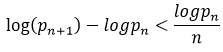 (4)
(4)
These are easily provable by direct analysis and are by no means a complete list. The left hand side of (2), however, is the nth prime gap 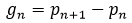 , and if the conjecture is correct,
, and if the conjecture is correct, 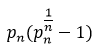 is an upper bound in terms of n for
is an upper bound in terms of n for 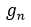 .
.
In fact, if (1) is accurate, an upper bound of 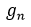 is found to be
is found to be 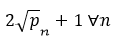 . (1) may also be used to improve on the Baker-Harman-Pintz's upper bound of
. (1) may also be used to improve on the Baker-Harman-Pintz's upper bound of 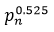 for
for  . More conjectural upper limits for
. More conjectural upper limits for  in terms of n will be showed, but for the time being, we will focus on certain known findings that give an approach to demonstrating (1).
in terms of n will be showed, but for the time being, we will focus on certain known findings that give an approach to demonstrating (1).
Evidence to back up the conjecture
Proving (1) for infinitely many n∈N:
Zhang demonstrated that,
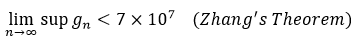
Outcome: There exists an infinite number of n∈N such that 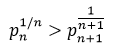
Proof: We assume 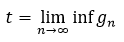 and
and 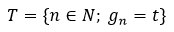
Then, according to Zhang's Theorem, T is infinite and
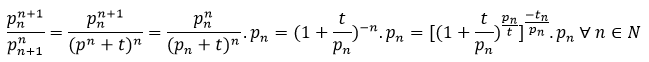
Now, 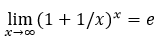
Specifically, for any sufficiently big n∈T, 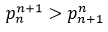 . This is identical to the statement of the theorem. Thus,
. This is identical to the statement of the theorem. Thus,
Zhang’s Theorem ⇒ (1) applies for infinitely many n ∈ N
Proving (1) for almost all n ∈ N:
In order to prove this statement, we will require the following two well-known theorems.
Theorem 1: Let us consider the set of the first n−1 differences between consecutive primes, i.e 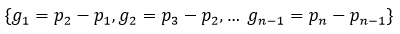 . Let
. Let 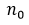 be the number of differences in this set such that
be the number of differences in this set such that 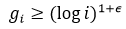 where ϵ > 0 is fixed. We then have the limit
where ϵ > 0 is fixed. We then have the limit 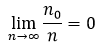 . Therefore, if
. Therefore, if 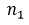 is the number of differences in this set such that
is the number of differences in this set such that 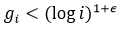 we have that
we have that 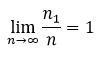 . That is, practically all of the set's differences
. That is, practically all of the set's differences 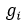 fulfil
fulfil 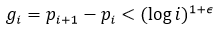
Theorem 2: The following asymptotic formula holds
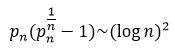
Proof: We have 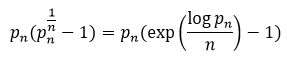 . The prime number theorem
. The prime number theorem 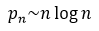 , consequently
, consequently 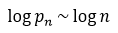 , derives directly from the formula exp(x)=1+x+o(x)(x→0). The theorem is proved.
, derives directly from the formula exp(x)=1+x+o(x)(x→0). The theorem is proved.
Outcome: The inequalities in (1) to (4) hold for practically all successive prime pairings 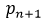 and
and  .
.
Proof: According to Theorem 2, since 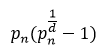 is asymptotically comparable to
is asymptotically comparable to 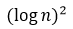 , there must be some value of n∈N, such that ∀j>n, j∈N,
, there must be some value of n∈N, such that ∀j>n, j∈N, 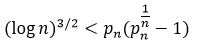 .
.
Furthermore, theorem 1 with ϵ=12 shows that for nearly all pairs of successive primes 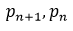 , the inequality
, the inequality  holds for almost all pairings of consecutive primes
holds for almost all pairings of consecutive primes 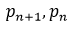 . This is inequality (2), and because (2) and (1) are similar, (1) holds true for almost all n∈N.
. This is inequality (2), and because (2) and (1) are similar, (1) holds true for almost all n∈N.
Upper boundaries of the prime gap function
The prime gap function, 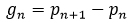 , is inextricably linked to Firoozbakht's conjecture. There are a few speculative upper bounds on
, is inextricably linked to Firoozbakht's conjecture. There are a few speculative upper bounds on 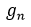 .
.
It is proved that 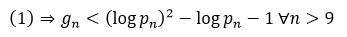
It can also be proven that 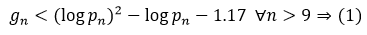
Following the demonstration of the previous implication, we shall show how (1) follows from the assumed reality of another such conjectural upper bound, one of a family of such bounds.
Outcome: 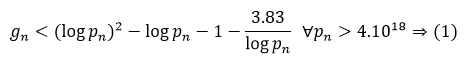
Proof: We notice that (1) has been proven for all primes less than 4x(10)^18, which is why we include it in the stated condition.
Using the Panaitopol formula for π(x), we get an upper bound for the prime-counting function π(x), which is provided by:
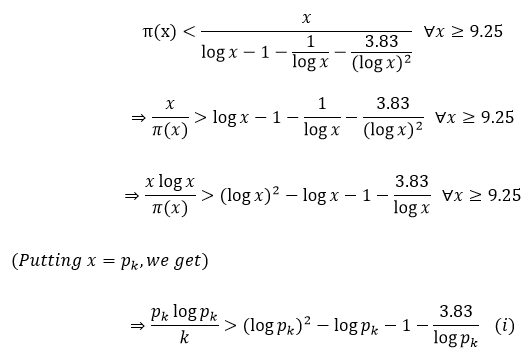
We are not including our x ≥ 9.25 constraint since we are examining primes higher than 4x(10)^18, and primes up to the limit have already been proven to obey the conjecture. As a result, the primes in question are large enough.
We know using calculus,
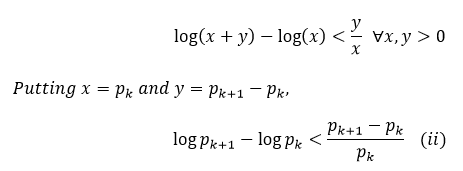
Thus we get from the given inequality,
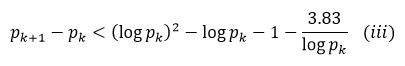
From (i), (ii) and (iii), we get,
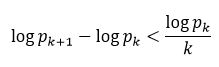
which is (4), one of the equivalent forms of (1). As a result, we have demonstrated that if the higher bound indicated above holds, then (1) is true.
There are two additional conjectured upper boundaries for  , which are as follows:
, which are as follows:
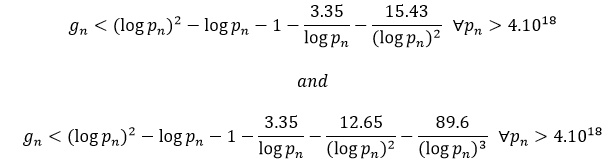
and the truth of either of these two implies (1).
Program to verify the conjecture
Following is a C++ Program to verify the conjecture:
#include <bits/stdc++.h>
using namespace std;
void firoozbakhtConjecture(int n)
{
bool prime[n + 1];
memset(prime, true, sizeof(prime));
for (int p = 2; p * p <= n; p++)
{
if (prime[p] == true)
{
for (int i = p * p; i <= n; i += p)
prime[i] = false;
}
}
double i=1;
for (int p = 2; p <= n; p++)
if (prime[p])
{
cout << double( pow(p,(1/i)) ) <<"\n";
i++;
}
}
int main()
{
int n = 100;
firoozbakhtConjecture(n);
return 0;
}
The above C++ program will yield the following output:
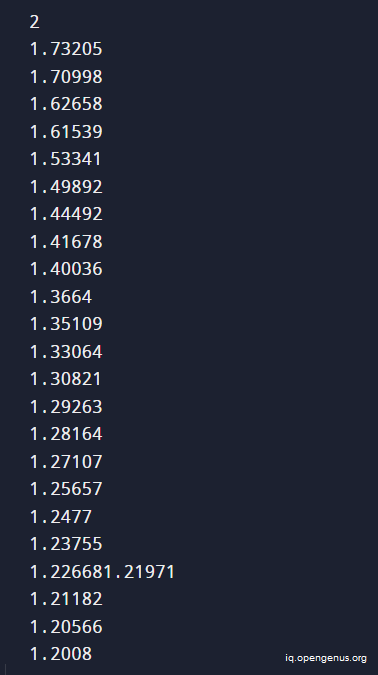
The series keeps on decreasing for a large range and hence the conjecture can be proved till that given range. You can run it continuously till two consequtive elements increase (which will disprove the conjecture).
These techniques are used to verify conjectures till a given limit.
Associated conjectures
Three more conjectures were proposed in relation to the Firoozbakht Conjecture.
The Nicholson Conjecture-
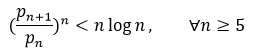
Forgues' Conjecture-
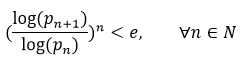
Farhadian Conjecture-
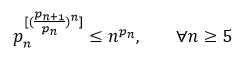
To see how these conjectures connect to the Firoozbakht Conjecture, consider the following inequalities:
Theorem 1:
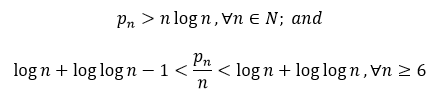
This inequality is know as the Rosser’s Theorem.
Theorem 2: Farhadian ⇒ Nicholson ⇒ Firoozbakht ⇒ Forgues
Proof Assume the Farhadian Conjecture is correct. Thereafter, using logarithms,
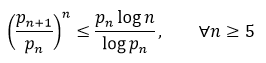
From previous theorem,
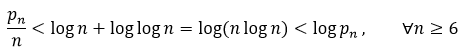
This suggests the Nicholson Conjecture. Assuming the Nicholson Conjecture, Rosser's Theorem states that
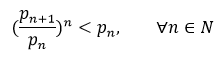
which is the same as
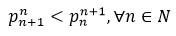
This corresponds to the Firoozbakht Conjecture. Taking logarithms out from previous inequality, we get
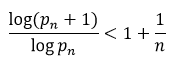
When we increase to the n-power, we obtain
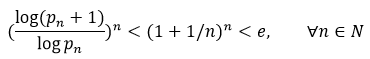
which is the Forgues Conjecture.
The Firoozbakht conjecture is one of the most powerful upper limits on prime gaps, rivalling the Cramér and Shanks conjectures. Cramér predicted that the gaps around p are no larger than 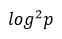 , while Shanks proposed the asymptotic equivalence
, while Shanks proposed the asymptotic equivalence 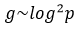 for maximal prime gaps g.
for maximal prime gaps g.
