
Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
Reading time: 35 minutes | Coding time: 15 minutes
Fusion tree is a tree data structure that implements associative array in a known universe size. Fusion trees, like Van Emde Boas Trees are used to solve predecessor and successor problem. While Emde Boas tree is useful when universe size is small, fusion tree is used when universe size is large, while providing linear space complexity.
Fusion tree is essentially a B-tree with degree wc where w is the word size and c is some constant smaller than 1. This means the a height of tree will be logwn where n is number of elements stored in the tree.
An important operation used by fusion trees is sketch which is used to compress w bit keys:
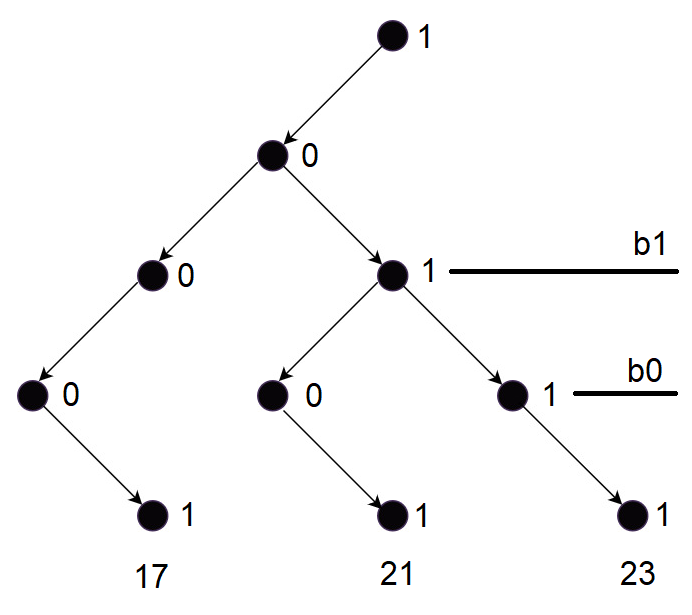
Consider the tree given above representing numbers 17, 21, 23. Let this be the fusion tree. Then the sketch operation would give the bits only at branching positions, which are labeled as b0 and b1 in above figure. In above figure, bit positions 1 and 2 (0 indexed) are the branching levels. So sketch will give bits at these position compressed into a single integer.
For example,
sketch(21) = sketch(10101) = 1 0 1 0 1 = 01
sketch(17) = sketch(10001) = 1 0 0 0 1 = 00
sketch(23) = sketch(10001) = 1 0 1 1 1 = 11
Considering a general case, we will get r sketch bits: b0, b1, ... br - 1.
Let c be 10 here giving a branching factor of k = w1/10, i.e. each node will have w1/10 - 1 keys and w1/10children. This is where sketch operation comes into play. Since it is not possible to compare all O(k) keys of a node in constant time, sketch operation compresses the keys for faster comparisons between all keys within a node allowing for constant time predecessor queries. Since there are k - 1 keys in a node, r is always less than k.
So the number of bits used to store the sketches of all the keys in a node is O(w2/10). Let keys be x0, x1, ... xk-1. Then sketch(x0) < sketch(x1) < ... < sketch(xk-1) since sketch only considers distinguishing bits.
This sketch is called exact sketch.
Algorithm
Sketch operation
- Sketch(x): In practice, approximate sketch is used instead of exact sketch because exact sketch cannot be computed in constant time. Prefect sketch requires the distinguishing bits to be compressed which a computation expensive operation. Approximate sketch doesn't try to compress the distinguishing bits together tightly, rather it adds a fixed pattern of zeroes between every two distinguishing bits. This is done by multiplication with a predetermined constant. The result will be of order O(r4) where r is count of distinguishing bits.
- Let Mask be the mask that will filter out distinguishing bits and m be a predetermined constant.
- x' = x AND Mask. After bitwise AND, x' will have only distinguishing bits.
- result = x' * m. Right shift result until it is r4 bits long. result is the approximate sketch.
To calculate the constant m, a inductive definition is used. Let bi, 0 <= i <= r - 1, be the distinguishing bit positions and Xbr - 1, Xbr - 2, ... ,Xb0 be set bits of the sketch of b. After multiplication of b with m, each bit at bi will be shifted to location bi + mi such that Xi = bi + mi . The word formed after multiplication must follow following properties:
- bi + mj are distinct for all pairs (i, j). This will make sure that no distinguishing bits overlap each other after multiplication.
- bi + mi is a strictly increasing with respect to i. This means that order of distinguishing bits, and thus the order of original words is preserved.
- (br-1 + mr-1) - (b0 + m0) <= r4, i.e. sketch is r4 bits long.
The basic strategy to make m is:
For every t, 0 <= t <= r-1, select smallest value for mt that satisfies mt != bi - bj + mk for every 0 <= i, j <= r-1 and 0 <= k <= t-1.
This is basically equivalent to bi + mj != bk + ml for 0 <= i, j, k , l <= r-1, thus satisfying condition 1. Selecting smallest integers first satisfies condition 2.
Since there are r3 possibilities for mt, condition 3 is also satisfied.
So m will a binary number with positions m0, ..., mr - 1 set as 1, and every 1's will have a padding of r3.
Parallel comparison
- Parallel comparison: Parallel comparison is used to find position of a value withing the set of keys in a node in constant time. A node will have atmost r + 1 keys. The sketches of all those keys can be concatenated to form a word. This word is used to compare query value q directly with all the keys at once rather than comparing with time one by one.
1. Let X0, X1, ... ,Xr be the keys.
2. Then the sketch of a node is 1sketch(X0)1sketch(X1)... 1sketch(Xr).
3. Convert sketch(a) to sketch(q)' = 0sketch(q)0sketch(q)... 0sketch(q).
4. After subtracting value at step 3 from value at step 2, we will get a number that
will be like : 0________0__ ... ___0________1________1________1. Call it diff.
6. There are 0's where sketch of Xi is less than sketch(q) and 1 when
Xi is greater than sketch(q). The dashes represent garbage bits where
sketch values used to be. It will always be a series of 0's followed by a series
of 1's since sketch operation maintains order of keys.The position where the
series of 0 turns into 1 is the position where sketch(q) should be placed.
So sketch(Xi) < sketch(q) < sketch(Xi + 1), when bit of diff for
sketch(Xi) = 0, and for sketch(Xi + 1) is 1Note that parallel comparison gives index such that sketch of k is tightly bound with the sketches of keys, not the keys itself.
Predecessor and Successor
- Predecessor and Successor: This is also called de-sketching. The algorithm below finds predecessor or successor of q in a node of fusion tree. It will be applied recursively to find children nodes until leaf node is reached.
1. Compute sketch(q), which will give approximate sketch of q.
2. Use parallel comparison to get Xi and Xi + 1 such that sketch(Xi) <= sketch(q) <= sketch(Xi + 1).
3. Find y = common prefix of (Xi or Xi + 1) and k.
4. For successor:
Append y with suffix 1000...000 to fill the non_common bits and store it in a
variable e. Then e = y100...00.
For example: let Xi = 0 1 1 0 0 1 0 1 1
and k = 0 1 1 0 0 0 0 0 0
then y = 0 1 1 0 0
and e = 0 1 1 0 0 1 0 0 0
For predecessor:
Append y with suffix 0111...11 to fill the non_common bits and store it in a
variable e. Then e = y011...11
5. Use parallel comparison to get Xj and Xj + 1 such that sketch(Xj) < sketch(e) < sketch(Xi + 1).
6. Predecessor of q = Xj.
Successor of q = Xj + 1After sketching, the order is maintained only for the keys. There is no gurantee that if sketch(Xi) < sketch(q) < sketch(Xi + 1) then Xi < q < Xi + 1. That is why steps 3 to 5 are used.
Insert
- insert(k): The insertion is almost exactly same as a normal B-tree insertion.
1. Start with current node as root node.
2. Use parallel search to find appropriate position for k. If current node is not
a leaf node, set current node as the child at found position. Repeat step 2.
3. Current node is now leaf node. Insert key into correct position. If number of
keys is more than max-keys, split the node at middle, and add key at mid
position to parent node, with it pointing to current node. If parent node
also exceeds max-keys, keep splitting until root is reached.
If the root node also exceeds man-keys, split root and make mid key as new
root.
4. If the keys in current node have been modified, recalculate node sketch and m.Complexity
- Time complexity:
- Find, Successor, Predecessor: O(logwN)
- Insert: O(log2w)
- Delete: O(log2w)
- Space complexity: O(N)
Where N is count of values stored and W is the size of word, i.e. size of data type used to store the values. Complexity of insertion and deletion depends heavily on the strategy used to implement dynamic properties.
Implementations
Python 3
class Node:
"""Class for fusion tree node"""
def __init__(self, max_keys = None):
self.keys = []
self.children = []
self.key_count = 0
self.isLeaf = True
self.m = 0
self.b_bits = [] # distinguishing bits
self.m_bits = [] # bits of constant m
self.gap = 0
self.node_sketch = 0
self.mask_sketch = 0
self.mask_q = 0 # used in parallel comparison
self.mask_b = 0
self.mask_bm = 0
self.keys_max = max_keys
if max_keys != None:
# an extra space is assigned so that splitting can be
# done easily
self.keys = [None for i in range(max_keys + 1)]
self.children = [None for i in range(max_keys + 2)]
class FusionTree:
"""Fusion tree class. initiateTree is called after all insertions in
this example. Practically, node is recalculated if its keys are
modified."""
def getDiffBits(self, keys):
res = []
bits = 0
for i in range(len(keys)):
if keys[i] == None:
break;
for j in range(i):
w = self.w
while (keys[i] & 1 << w) == (keys[j] & 1 << w) and w >= 0:
w -= 1
if w >= 0:
bits |= 1 << w
i = 0
while i < self.w:
if bits & (1 << i) > 0:
res.append(i)
i += 1
return res
def getConst(self, b_bits):
r = len(b_bits)
m_bits = [0 for i in range(r)]
for t in range(r):
mt = 0
flag = True
while flag:
flag = False
for i in range(r):
if flag:
break
for j in range(r):
if flag:
break
for k in range(t):
if mt == b_bits[i] - b_bits[j] + m_bits[k]:
flag = True
break
if flag == True:
mt += 1
m_bits[t] = mt
m = 0
for i in m_bits:
m |= 1 << i
return m_bits, m
def getMask(self, mask_bits):
res = 0
for i in mask_bits:
res |= 1 << i
return res
def initiateNode(self, node):
if node.key_count != 0:
node.b_bits = self.getDiffBits(node.keys)
node.m_bits, node.m = self.getConst(node.b_bits);
node.mask_b = self.getMask(node.b_bits)
temp = []
# bm[i] will be position of b[i] after its multiplication
# with m[i]. mask_bm will isolate these bits.
for i in range(len(node.b_bits)):
temp.append(node.b_bits[i] + node.m_bits[i])
node.mask_bm = self.getMask(temp);
# used to maintain sketch lengths
r3 = int(pow(node.key_count, 3))
node.node_sketch = 0
sketch_len = r3 + 1
node.mask_sketch = 0
node.mask_q = 0
for i in range(node.key_count):
sketch = self.sketchApprox(node, node.keys[i])
temp = 1 << r3
temp |= sketch
node.node_sketch <<= sketch_len
node.node_sketch |= temp
node.mask_q |= 1 << i * (sketch_len)
node.mask_sketch |= (1 << (sketch_len - 1)) << i * (sketch_len)
return
def sketchApprox(self, node, x):
xx = x & node.mask_b
res = xx * node.m
res = res & node.mask_bm
return res
def __init__(self, word_len = 64, c = 1/5):
# print(word_len)
self.keys_max = int(pow(word_len, c))
self.keys_max = max(self.keys_max, 2)
self.w = int(pow(self.keys_max, 1/c))
self.keys_min = self.keys_max // 2
print("word_len = ", self.w, " max_keys = ", self.keys_max)
self.root = Node(self.keys_max)
self.root.isLeaf = True;
def splitChild(self, node, x):
# a b-tree split function. Splits child of node at x index
z = Node(self.keys_max)
y = node.children[x] # y is to be split
# pos of key to propagate
pos_key = (self.keys_max // 2)
z.key_count = self.keys_max - pos_key - 1
# insert first half keys into z
for i in range(z.key_count):
z.keys[i] = y.keys[pos_key + i + 1]
y.keys[pos_key + i + 1] = None
if not y.isLeaf:
for i in range(z.key_count + 1):
z.children[i] = y.children[pos_key + i + 1]
y.key_count = self.keys_max - z.key_count - 1
# insert key into node
node.keys[x] = y.keys[pos_key]
# same effect as shifting all keys after setting pos_key
# to None
del y.keys[pos_key]
y.keys.append(None)
# insert z as child at x + 1th pos
node.children[x + 1] = z
node.key_count += 1
def insertNormal(self, node, k):
# print(node, node.keys,'\n', node.key_count)
# insert k into node when no chance of splitting the root
if node.isLeaf:
i = node.key_count
while i >= 1 and k < node.keys[i - 1]:
node.keys[i] = node.keys[i - 1]
i -= 1
node.keys[i] = k
node.key_count += 1
return
else:
i = node.key_count
while i >= 1 and k < node.keys[i - 1]:
i -= 1
# i = position of appropriate child
if node.children[i].key_count == self.keys_max:
self.splitChild(node, i)
if k > node.keys[i]:
i += 1
self.insertNormal(node.children[i], k)
def insert(self, k):
# This insert checks if splitting is needed
# then it splits and calls normalInsert
# if root needs splitting, a new node is assigned as root
# with split nodes as children
if self.root.key_count == self.keys_max:
temp_node = Node(self.keys_max)
temp_node.isLeaf = False
temp_node.key_count = 0
temp_node.children[0] = self.root
self.root = temp_node
self.splitChild(temp_node, 0)
self.insertNormal(temp_node, k)
else:
self.insertNormal(self.root, k)
def successorSimple(self, node, k):
i = 0
while i < node.key_count and k > node.keys[i]:
i += 1
if i < node.key_count and k > node.keys[i]:
return node.keys[i]
elif node.isLeaf:
return node.keys[i]
else:
return self.successor2(node.children[i], k)
def parallelComp(self, node, k):
# this function should basically give the index such
# that sketch of k lies between 2 sketches
sketch = self.sketchApprox(node, k)
# This will give repeated sketch patterns to allow for comparison
# in const time
sketch_long = sketch * node.mask_q
res = node.node_sketch - sketch_long
# mask out unimportant bits
res &= node.mask_sketch
# find the leading bit. This leading bit will tell position i of
# such that sketch(keyi-1) < sketch(k) < sketch(keyi)
i = 0
while (1 << i) < res:
i += 1
i += 1
sketch_len = int(pow(node.key_count, 3)) + 1
return node.key_count - (i // sketch_len)
def successor(self, k, node = None):
if node == None:
node = self.root
if node.key_count == 0:
if node.isLeaf:
return -1
else:
return self.successor(k, node.children[0])
# the corner cases are not concretely defined.
# other alternative to handle these would be to have
# -inf and inf at corners of keys array
if node.keys[0] >= k:
if not node.isLeaf:
res = self.successor(k, node.children[0])
if res == -1:
return node.keys[0]
else:
return min(node.keys[0], res)
else:
return node.keys[0]
if node.keys[node.key_count - 1] < k:
if node.isLeaf:
return -1
else:
return self.successor(k, node.children[node.key_count])
pos = self.parallelComp(node, k)
# print("pos = ", pos)
if pos >= node.key_count:
print(node.keys, pos)
dump = input()
if pos == 0:
pos += 1
# x = node.keys[pos]
# find the common prefix
# it can be guranteed that successor of k is successor
# of next smallest element in subtree
x = max(node.keys[pos - 1], node.keys[pos])
# print("x = ", x)
common_prefix = 0
i = self.w
while i >= 0 and (x & (1 << i)) == (k & (1 << i)):
# print(i)
common_prefix |= x & (1 << i)
i -= 1
if i == -1:
return x
temp = common_prefix | (1 << i)
pos = self.parallelComp(node, temp)
# if pos == 0:
# possible error?
# pos += 1
# print("pos = ", pos, bin(temp))
if node.isLeaf:
return node.keys[pos]
else:
res = self.successor(k, node.children[pos])
if res == -1:
return node.keys[pos]
else:
return res
def predecessor(self, k, node = None):
if node == None:
node = self.root
if node.key_count == 0:
if node.isLeaf:
return -1
else:
return self.predecessor(k, node.children[0])
# the corner cases are not concretely defined.
# other alternative to handle these would be to have
# 0 and inf at corners of keys array
if node.keys[0] > k:
if not node.isLeaf:
return self.predecessor(k, node.children[0])
else:
return -1
if node.keys[node.key_count - 1] <= k:
if node.isLeaf:
return node.keys[node.key_count - 1]
else:
ret = self.predecessor(k, node.children[node.key_count])
return max(ret, node.keys[node.key_count - 1])
pos = self.parallelComp(node, k)
if pos >= node.key_count:
print(node.keys, pos, "ERROR? pos > key_count")
dump = input()
if pos == 0:
pos += 1
# find the common prefix
# it can be guranteed that successor of k is successor
# of next smallest element in subtree
x = node.keys[pos]
common_prefix = 0
i = self.w
while i >= 0 and (x & (1 << i)) == (k & (1 << i)):
common_prefix |= x & (1 << i)
i -= 1
if i == -1: # i.e. if x is exactly equal to k
return x
temp = common_prefix | ((1 << i) - 1)
pos = self.parallelComp(node, temp)
if pos == 0:
if node.isLeaf:
return node.keys[pos]
res = self.predecessor(k, node.children[1])
if res == -1:
return node.keys[pos]
else:
return res
if node.isLeaf:
return node.keys[pos - 1]
else:
res = self.predecessor(k, node.children[pos])
if res == -1:
return node.keys[pos - 1]
else:
return res
def initiate(self, node):
if node == None:
node = Node(self.keys_max)
self.initiateNode(node)
if not node.isLeaf:
for i in range(node.keys_max + 1):
self.initiate(node.children[i])
def initiateTree(self):
self.initiate(self.root)
if __name__ == "__main__":
# create a fusion tree of degree 3
tree = FusionTree(243)
tree.insert(1)
tree.insert(5)
tree.insert(15)
tree.insert(16)
tree.insert(20)
tree.insert(25)
tree.insert(4)
print(tree.root.keys)
for i in tree.root.children:
if i is not None:
print (i, " = ", i.keys)
if not i.isLeaf:
for j in i.children:
if j is not None:
print( j.keys)
tree.initiateTree()
# the tree formed should be like:
# [| 5 | | 16 |]
# / | \
# / | \
# [1, 4] [15] [20, 25]
print("\nKeys stored are:")
print("1, 4, 5, 15, 16, 20, 25\n")
print("Predecessors:")
for i in range(26):
print(i, "------------------->", tree.predecessor(i), sep = '\t')
print("Successor:")
for i in range(26):
print(i, "------------------->", tree.successor(i), sep = '\t')
Applications
- Fusion tree are used extensively in database systems.
- Fusion tree and Van Emde boas tree are together. When word size is large, fusion tree are used. When word size is smaller, Van Emde Boas tree is used.
References/ Further reading
- Try to change insert function to use parallel comparison as an exercise.
