Cartesian tree sorting

Reading time: 30 minutes | Coding time: 20 minutes

Algorithm

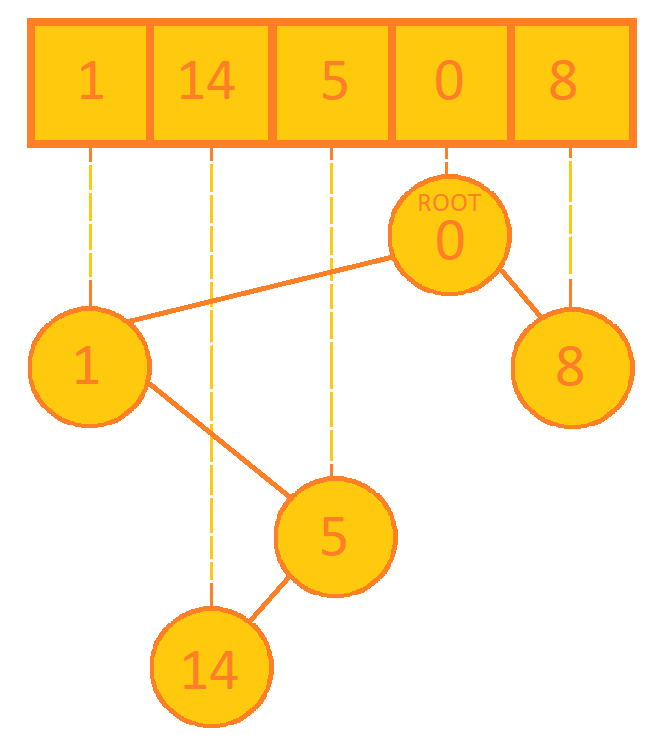
1. Construct a Cartesian tree for given sequence.
2. Create a priority queue, initially having only the root of Cartesian tree.
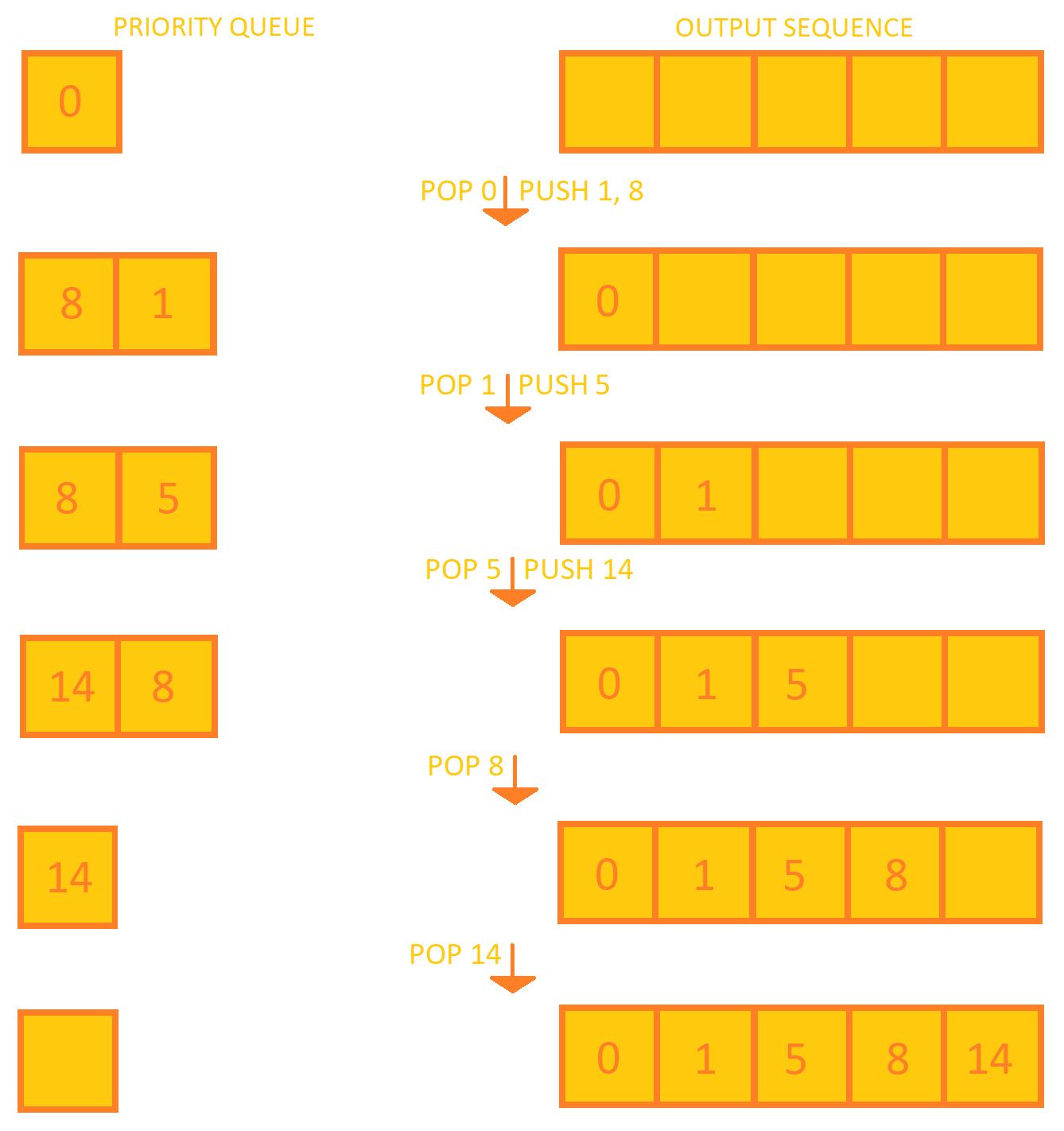
3. Pop the minimum value x from the priority queue
4. Add x to the output sequence
5. Push the left child of x from Cartesian tree into priority queue.
6. Push the right child of x from Cartesian tree into priority queue.
7. If priority queue is not empty, goto step 3.

The Cartesian tree sorting for the sequence {1, 14, 5, 0, 8} will be:

Complexity

• Worst case time complexity: Θ(NlogN)
• Best case time complexity: O(N)
• Space complexity: O(N)

Implementations

C++ 11

/*
 * c++ 11 code to construct a Cartesian tree. The method cartesianTreeSort
 * will sort the contents of the array.
 */

#include <iostream>
#include <vector>
#include <queue>

struct Node{
    int value;
    Node *left, *right;
    Node *parent;

    Node(){
        value = 0;
        parent = NULL;
        left = NULL;
        right = NULL;
    }
};

// Used by priority queue
struct compare{
    bool operator()(Node *left, Node *right){
        return left->value > right->value;
    }
};

class CartesianTree{
private:
    // last pointer to keep track of last node added
    Node *root, *last;

    Node * findLowestNode(Node *node, int x){
        if(node->value < x)
            return node;
        else if(node->parent != NULL)
            return findLowestNode(node->parent, x);
        else
            return NULL;
    }

public:
    Node * getRoot(){
        return root;
    }

    void addNode(int x){
        Node *new_node = new Node;
        new_node->value = x;
        if(root == NULL){
            last = new_node;
            root = new_node;
            return;
        }
        Node *z = findLowestNode(last, x);
        if(z == NULL){
            new_node->left = root;
            root->parent = new_node;
            root = new_node;
        }
        else{
            new_node->left = z->right;
            z->right = new_node;
            new_node->parent = z;
        }
        last = new_node;
    }

    CartesianTree(std::vector<int> ar){
        root = NULL;
        last = NULL;
        // Call addNode function for each element of the array
        for(auto x : ar){
            addNode(x);
        }
    }

    void InorderTraversal(Node *node){
        // To print inorder traversal of the tree
        if(node == NULL)
            return;
        InorderTraversal(node->left);
        std::cout << node->value << ' ';
        InorderTraversal(node->right);
    }

    // Function to sort and store values in array
    void cartesianTreeSort(std::vector<int> &sorted_ar){
        // Initialize input array
        sorted_ar.assign(0, 0);

        // Initialize priority queue
        std::priority_queue<Node *, std::vector<Node *>, compare> p_queue;
        p_queue.push(root);
        Node *temp = NULL;
        while(!p_queue.empty()){
            temp = p_queue.top();
            p_queue.pop();
            sorted_ar.push_back(temp->value);
            if(temp->left){
                p_queue.push(temp->left);
            }
            if(temp->right){
                p_queue.push(temp->right);
            }
        }
    }
};

int main(){
    std::vector<int> ar = {1, 14, 5, 0, 8};

    CartesianTree tree(ar);
    std::cout << "Inorder Traversal\n";
    tree.InorderTraversal(tree.getRoot());
    std::cout << '\n';

    std::vector<int> sorted;
    tree.cartesianTreeSort(sorted);
    std::cout << "Sorted array is\n";
    for(auto x : sorted)
        std::cout << x << ' ';
    std::cout << '\n';
}

Applications

• It is possible to quantify how much faster algorithm will run than O(nlogn) using a measurement called oscillation. Practically, the complexity is close to O(nlog(Osc)) where Osc is oscillation.
• Oscillation is small if the sequence is partially sorted, thus the algorithm performs faster with partially sorted sequences.

References/ Further reading

• Paper by Levcopoulos and Petersson on the algorithm.
• An interesting article by David Eppstein comparing Cartesian tree sort and splaysort.