Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
Graph neural network (GNN) is a special kind of network, which works with a graph as a data sample. The typical neural network works with arrays, while GNN works with graphs.
Now before we dive into the technicalities of GNN, let us (re)visit graphs.
Graphs are nothing but the connection of various nodes (vertices) via edges. The nodes, as well as edges, have their values depending on the data.
Mathematically graphs are represented as a function of vertices and edges like follows:
G = Ω (V,E)
The function omega is what defines the relationships between the edges and vertices. The function can be anything at all. Do keep in mind this what determines the operations you can perform on any of the nodes in the graph.
Now let us come back to GNN. Every node in the GNN is operated on, by a single recurrent unit. To put it shortly, recurrent units are the units that take the inputs from the data as well as from the output of the previous iteration.
When we put these recurrent units into the graph, we need to define: the inputs to the nodes and how the output would be calculated.
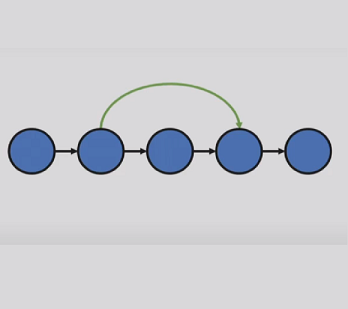
GNNs work on the principle of message passing or technically speaking, data aggregation. What it does is that it takes the inputs from all the neighboring nodes, and then computes the value for the current node. Take the following image for example.
Here, each node is a recurrent unit, and every node takes the inputs from the neighboring nodes (message). To compute the node, we first sum up (aggregate) all the neighbor node values and then pass it to the function of computation (here G(v)).
Now at first, the node would only know about its direct neighbors and the inputs would be taken accordingly. But what if we want to connect more nodes with a particular node? We increase the reach iteratively. This is also known as unrolling. See the image below, which is of adjacency of 1. The circles represent the reach of the node at the center.
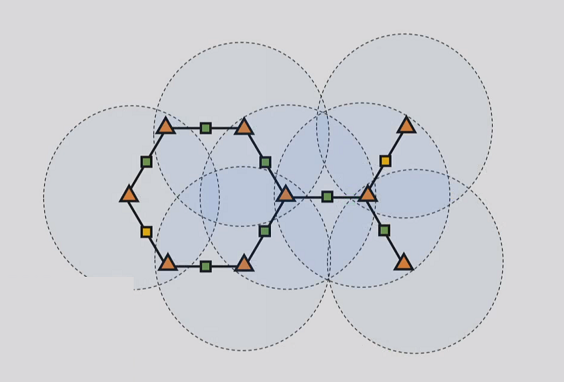
It is obvious but important to note that with the increase in adjacency, the number of nodes in contact would also increase.
But then what is the final output?
We should note that a graph is an interconnected network of nodes. It does not have a start point and an endpoint. But the overall output depends on the application in which GNN is used. For example, sometimes the overall representation after all iterations could be the output. Sometimes knowledge and importance of one node to the other is the output. So, the final output can also be simply defined as a value of the summation of all nodes.
So, summing it all up. The GNN works on the principle of data aggregation, meaning, it takes the values of the adjacent nodes (value of which is controlled by adjacency). Once we increase the value of adjacency, the number of nodes in contact would increase. To compute the value of the node, we pass the summation of values of all adjacent nodes and pass it through a function. That’s all.
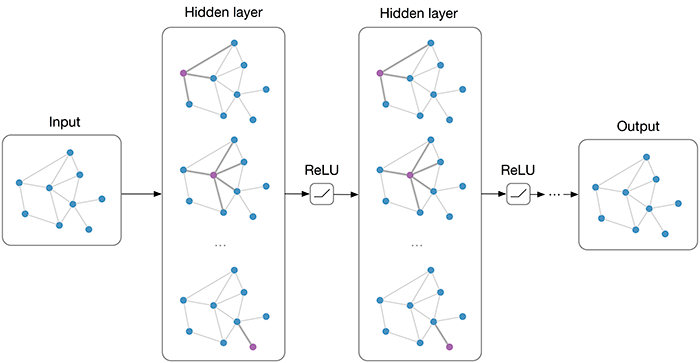
If we want to look at the architecture of each iteration and overall network and how it all changes, we may look at the following image.
Now, where can all this be used?
Use cases
GNNs can be used in all the applications which work on graph-based data. For example, social networks. But how exactly?
- In any social media application, it is really important to connect people. And one of the greatest usages in social media applications is something called as the feed. The feed is decided based on the connections of the particular user (node). So, each user or node, would aggregate the data from all the adjacent nodes and then pass it through a function to decide the feed.
- Not just feed, but also other cases like a recommendation of friend or connection.
Other than social media, we can also use these networks in applications of logistics, for better route information.
Let us now go and evaluate these networks precisely with some advantages and limitations.
Pros and Cons
Let me ask you something, what is the difference between the two graphs provided below.
Image-1
Image-2
None. Other than the way of representation. But of course, the representation does affect the way we store the data traditionally. That is why we needed the graph networks in the first place.
-
The second thing is the quantity of data. If we think about the overall mechanism of graph data structure and the kind of data it stores, it is huge if we try and convert it into some other form like an array. The sole reason being too much information to be clarified. Such as, which node is connected to which by which edge with what value. But if we directly take graphs like the sample points, it is fairly easy and inexpensive to store and process the data as compared to traditional neural networks.
-
Third, the GNNs outperforms many state-of-the-art algorithms when it comes to specialized cases, mentioned above, in the use cases. And this is because of the ability to work easily with graph-based data.
-
And lastly, the GNNs have a huge advantage which is directly linked with its structure. Which is that it can adaptively learn the importance of each neighbor.
However, GNNs are not at all flawless. When it comes to the limitations, one should surely look at the paper of How powerful are GNNs, to better understand those cases where it fails.
-
One such example as per the paper is the mean and max layers in the convolutional nets with GNN. In this, due to the limited and shallow learnings, it does affect the way the mean and max are calculated. It hinders the accuracy of the network because it is not able to place the values accurately enough.
-
Another problem is the computational expense. Even though we use graphs as the data structure, the computational toll would increase with each iteration and updating of weights. As shown earlier, with each iteration each node would have even more nodes in its information box, which will further increase the relations and number of weights to calculate for each node.
GNN is still somewhat of an unexplored field and it will take some time and application, to better understand the overall disadvantages of them in various cases. But it does give a base for a field which can make the logistics and netowrk based architectures even more accurate.
With this article at OpenGenus, you must have a good understanding of Graph Neural Networks in general. Enjoy.