Introduction to Clustering Algorithms

Clustering is one of the most popular applications in data analytics, and involves the division of the dataset into a number of groups such that each group has some distinctive characteristics, and the data points that belong to a particular group have characteristics similar to other points within the same group than those outside it. In machine learning terms, clustering is an unsupervised learning problem, since it seeks to classify or divide a dataset based on attributes of the points themselves rather than any given labels.

Clustering Approaches

It would be wrong to call clustering an algorithm, because it is in fact the problem to be solved using various different algorithms. Some approaches taken towards clustering are:

• Hard Clustering: Also called discrete clustering. Here, we consider each data point belongs either entirely to a particular cluster or not at all. This is great for datasets which are well-defined and not overlapping in nature.
• Fuzzy (Soft) Clustering: This approach takes into account the idea that a data point could belong to more than one cluster. Instead of directly assigning a cluster to a point, we generally assign a set of probability values to it based on how likely it is to appear in a particular cluster.
• Connectivity Models: These models assume that data points that are located close to each other in the data space are likely to exhibit more similarities to each other than to points far away from them. You may have guessed already that these are used to implement hierarchical clustering.
• Distribution Models: These models expect that data points in the same cluster are likely to exhibit the same kind of probability distribution (Gaussian/Normal/Bernoulli/Binomial/Poisson distributions etc). A good example of the same is the Expectation-maximization algorithm.
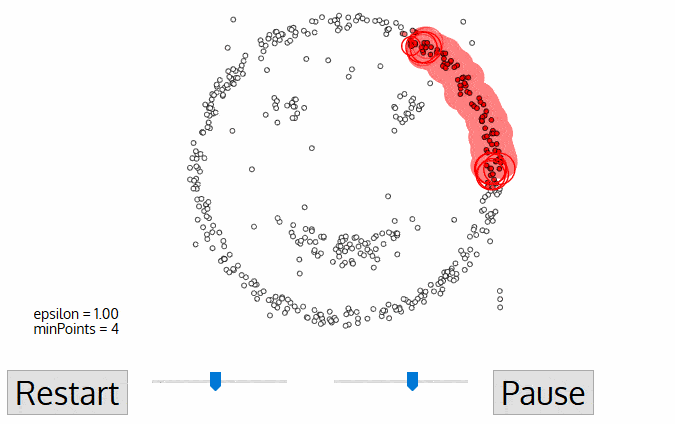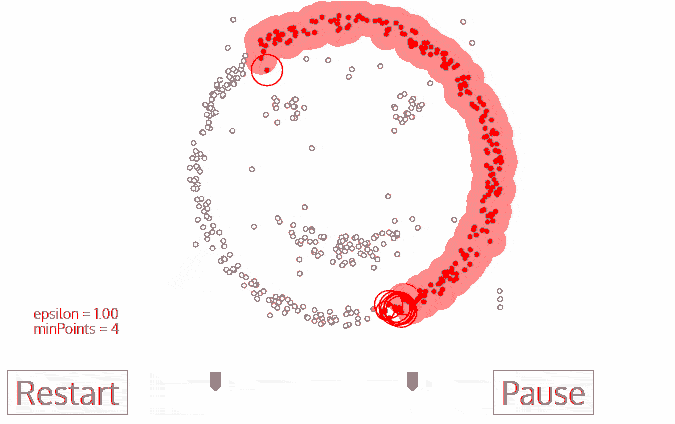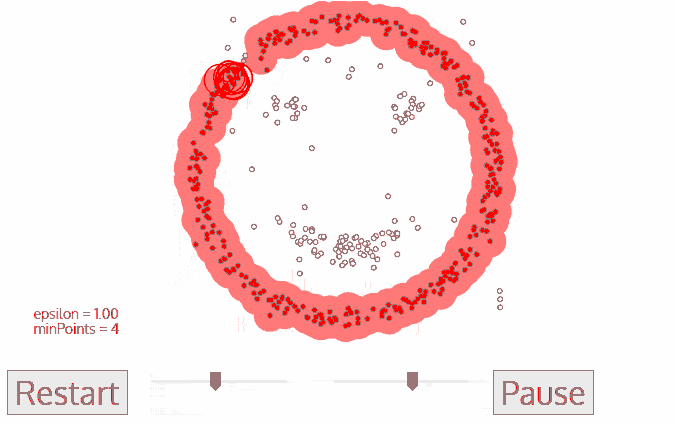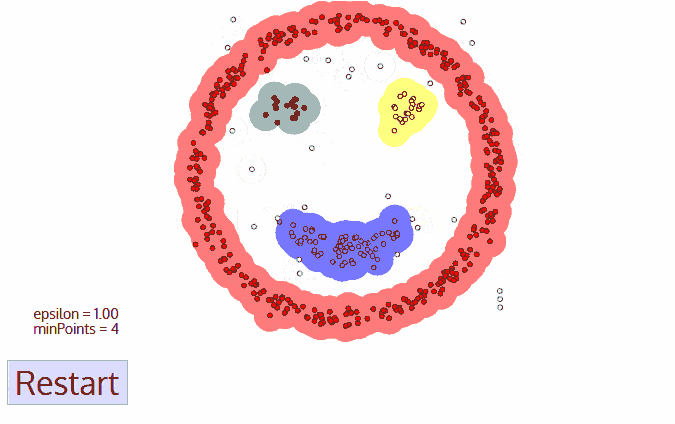
• Density Models: The models scan the data space and find regions with different densities, assigning all points within a particular region to the same cluster. OPTICS and DBSCAN are popular density models.
• Centroid Models: These start by assigning a cluster-centre or centroid to each cluster and then evaluate the most likely cluster for a data point based on its proximity to existing centroids. Needless to say, this is an iterative process, generally terminated when two successive iterations return the same clustering as an output. We are also required to know the number of desired clusters beforehand. The K-means algorithm is hence a centroid model-based algorithm.

One of the objectives of clustering is to minimize the intra-cluster distance (a metric measuring the distance between elements in a cluster, usually the maximal distance between any two elements) and maximize the inter-cluster distance (distance between two cluster centroids or boundary elements). It is worth noting that not only do these distance measures depict a variety of different distances, they are also calculated in different ways. The popular techniques are as follows:

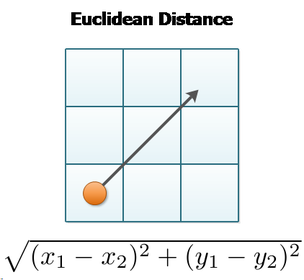
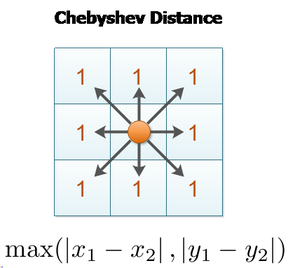
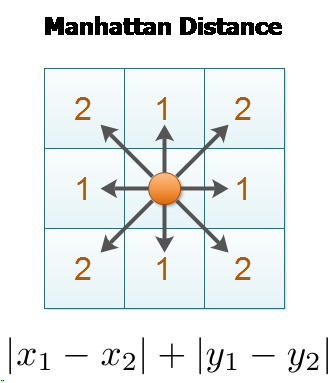
Some other popular distance metrics that are not explored here are maximum distance and Mahalanobis distance.

Clustering Algorithms

Having discussed some approaches, we must also look at specific algorithms used for clustering. At present, there are more than 100 documented clustering algorithms. Some of the popular and effective ones are:

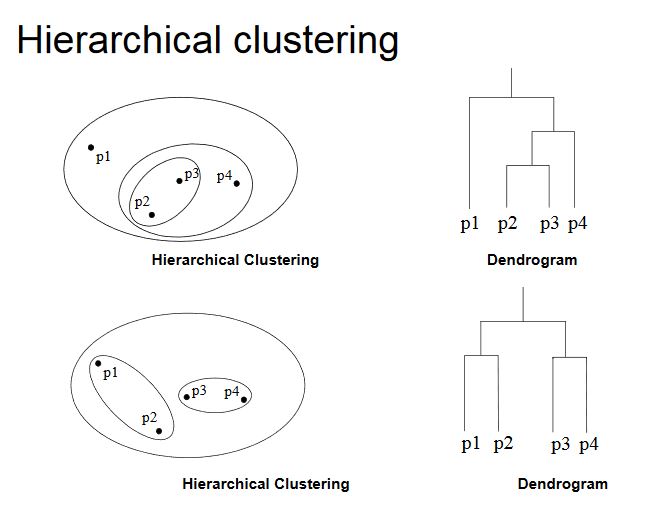
• Hierarchical Clustering Algorithms: This approach allows us to establish new clusters based on previously established clusters, thus refining the result at each step. Hierarchical clustering treats the dataset as a group of nested clusters visualized as a tree (often using a tool called the dendrogram diagram). This can be further subdivided into two approaches:

  • Agglomerative or Bottom-Up Clustering: We start by considering n clusters, each with one of the n elements in it, and then merge them into successively larger clusters based on similarity to established clusters.
  • Divisive or Top-Down Clustering: We start with the whole set as the master cluster, and with each iteration divide it into smaller clusters.

  

• Partitional Clustering Algorithms: Unlike hierarchical clustering, partitional clustering seeks to decompose the dataset into a predetermined k number of clusters, such that each object belongs to a single cluster only. K-means clustering is the best and most popular example of hard partitional clustering, while fuzzy c-means is the same for soft partitional clustering.
  
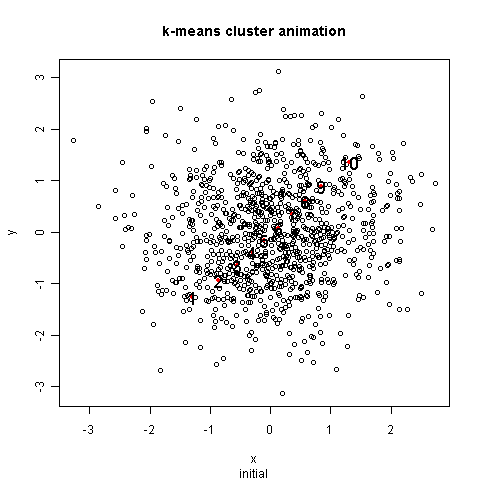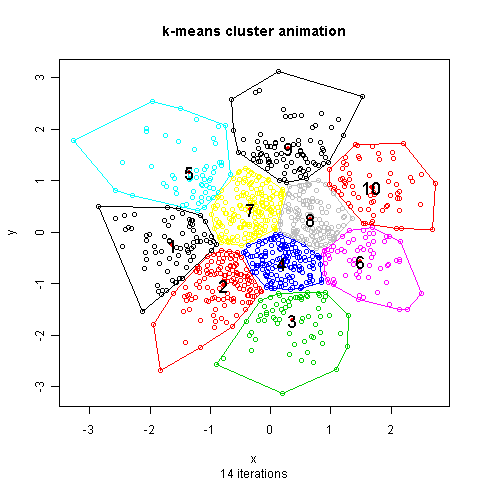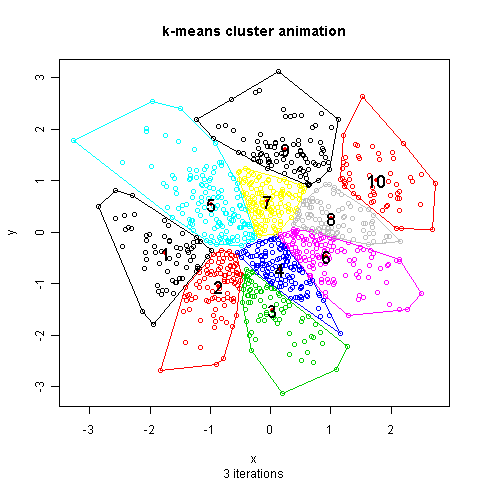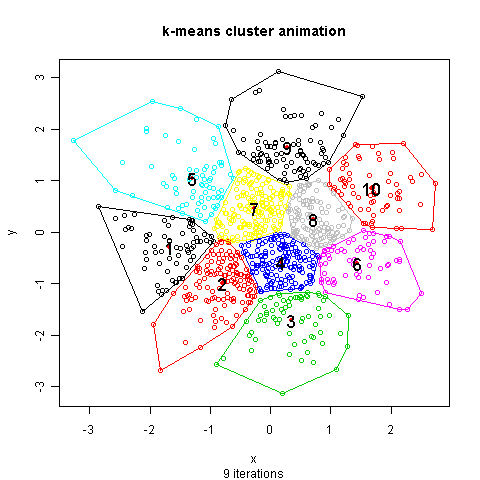
  Source (http://mcube.nju.edu.cn/jokergoo/animation-of-kmeans-clustering.html)

• Mean Shift clustering: A sliding window approach following density models.
  

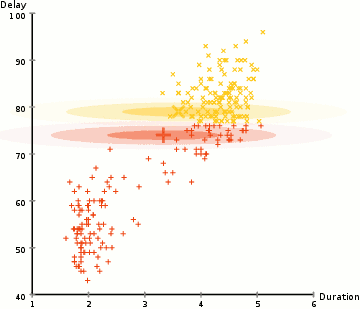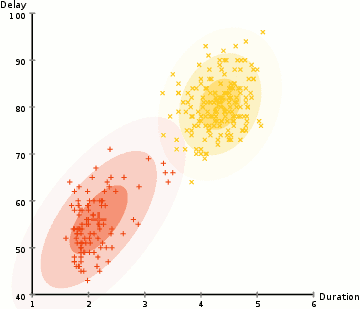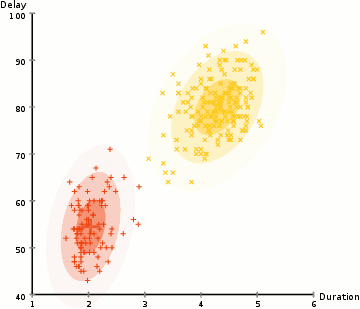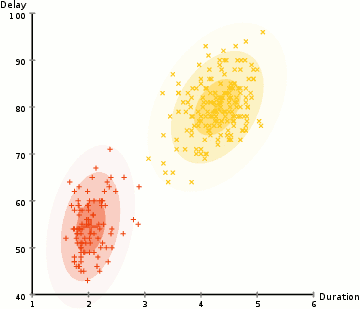
• Expectation–Maximization (EM) Clustering: A probability-based approach that fixes many of the issues with K-means (like the approach of repositioning cluster centres by averaging out all the points) by assuming a Gaussian probability distribution thus making it much more flexible and resistant to overlapping clusters.
  

• Density-Based Spatial Clustering of Applications with Noise (DBSCAN): Also based on density models
  

Applications

Clustering finds widespread application in a number of analytical domains, like:

• Market segmentation or dividing consumers into categories that can then be used for targeted campaigns.
• Recommendation engines
• Image Segmentation and Processing
• Outlier Analysis/Anomaly Detection
• Social Network Analysis