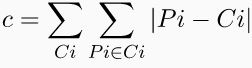Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
Reading time: 30 minutes | Coding time: 15 minutes
K-medoids Clustering is an Unsupervised Clustering algorithm that cluster objects in unlabelled data.
In this article, we are going to see What is K-medoids Clustering? And why we need it? First of all, come to our second question's answer: We need it because there are some cons in K-means Clustering i.e. in this an object with an extremely large value may substantially distort the distribution of objects in clusters/groups. Hence, it is sensitive to Outliers. It is resolved by K-medoids Clustering also known as an improvised version of K-means Clustering.
In K-medoids Clustering, instead of taking the centroid of the objects in a cluster as a reference point as in k-means clustering, we take the medoid as a reference point. A medoid is a most centrally located object in the Cluster or whose average dissimilarity to all the objects is minimum. Hence, the K-medoids algorithm is more robust to noise than the K-means algorithm.
There are three algorithms for K-medoids Clustering:
- PAM (Partitioning around medoids)
- CLARA (Clustering LARge Applications)
- CLARANS ("Randomized" CLARA).
Among these PAM is known to be most powerful and considered to be used widely. However, PAM has a drawback due to its time complexity (which we will discuss later). So, in this article, we are going to see the PAM algorithm in detail.
Algorithm
We now move to see what's going on inside the k-medoids Algorithm, which is as follows:
STEP1: Initialize k clusters in the given data space D.
STEP2: Randomly choose k objects from n objects in data and assign k objects to k clusters such that each object is assigned to one and only one cluster. Hence, it becomes an initial medoid for each cluster.
STEP3: For all remaining non-medoid objects, compute the Cost(distance as computed via Euclidean, Manhattan, or Chebyshev methods) from all medoids.
STEP4: Now, Assign each remaining non-medoid object to that cluster whose medoid distance to that object is minimum as compared to other clusters medoid.
STEP5: Compute the total cost i.e. it is the total sum of all the non-medoid objects distance from its cluster medoid and assign it to dj.
STEP6: Randomly select a non-medoid object i.
STEP7: Now, temporary swap the object i with medoid j and Repeat STEP5 to recalculate total cost and assign it to di.
STEP8: If di<dj then make the temporary swap in STEP7 permanent to form the new set of k medoid. Else undo the temporary swap done in STEP7.
STEP9: Repeat STEP4,STEP5,STEP6,STEP7,STEP8. Until no change;
Demonstration
Let's consider the following example:
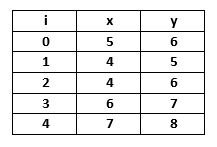
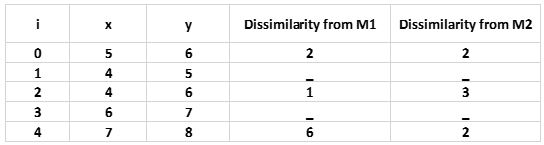
We take a small data set which contains only 5 Objects:
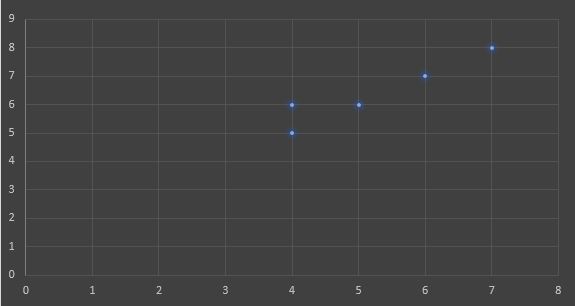
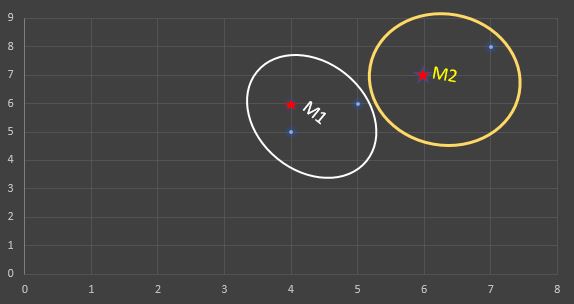
If a graph is drawn using the above data objects, we obtain the following:
Step1: Initialize number of clusters k = 2. Let the randomly selected two medoids be M1 (4,6) and M2 (6,7).
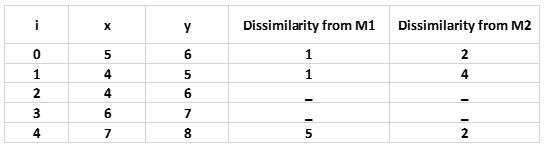
Step2: Calculate Cost. The dissimilarity of each non-medoid object with the medoids is calculated and tabulated:
For simplicity, we will take here Manhattan distance as our cost measure:
Each object is assigned to the cluster of that medoid whose dissimilarity is less.
The objects 0,1 go to cluster M1 and object 4 go to cluster M2.
The total cost:
(dj) = (1+1) + (2) = 3
Step3: Now randomly select one non-medoid object and recalculate the Cost. Let the randomly selected non-medoid object be (4,5) and take it as a candidate for medoid. The dissimilarity of each non-medoid object with the medoids M1(4,5) and M2(6,7) is calculated and tabulated:
Each object is assigned to the cluster of that medoid whose dissimilarity is less.
The objects 0,2 go to cluster M1 and object 4 go to cluster M2.
The total cost:
(di) = (2+1) + (2) = 5
Since, di > dj which is not satisfying the condition di < dj. So, We undo the swap. Hence (4,6) and (6,7) are the final medoids. The Clustering would be in the following way:
Complexity
- Total possibilities for a node: k*(n-k)
- Cost to compute E: (n-k)
- Total cost for each node:
k*(n-k)^2
Since time complexity for each iteration:
; where n is the number of objects in data, k is the number of clusters. Therefore, PAM works efficiently for small data sets but does not scale well for large data sets.
Implementation
To visualize K-medoids clustering, we here use basic Python from scratch so the key concepts don't leave weak and to develop the basic understanding about what's going on. We performs clustering on the Iris dataset, which you can read about here: archive.ics.uci.edu/ml/datasets/iris
Here is the core function of the k-medoids Clustering program which exactly shows the working of an algorithm:
def kmedoids_run(X, n_clusters, dist_func, max_iter=1000, tol=0.001):
# Get initial Medoid
n_samples, n_features = X.shape
# Here get_medoid() function Return random objects as initial medoid
md = get_medoid(n_clusters,n_samples)
if verbose:
print('Initial medoids are ', md)
medoids = md
# Here get_cost() function Return Total cost(dj) and cost of each cluster
members, costs, dj, dist_mat = get_cost(X, md,dist_func)
swap = True
count = 0
while True:
swap = False
for i in range(n_samples):
if not i in medoids:
for j in range(len(medoids)):
medoids_ = deepcopy(medoids)
medoids_[j] = i
# Here get_cost() function Return Total cost(di) and cost of each cluster
members_, costs_, di, dist_mat_ = get_cost(X, medoids_,dist_func)
if di-dj < tol:
members, costs, dj, dist_mat = members_, costs_, di, dist_mat_
medoids = medoids_
swap = True
print('Change medoids to ', medoids)
if count > max_iter:
print('End Searching by reaching maximum iteration', max_iter)
break
if not swap:
print('End Searching by no swaps')
break
count += 1
return medoids,members, costs, dj, dist_mat
# Return Final medoids , cost and members of each cluster and Final total cost(dj)
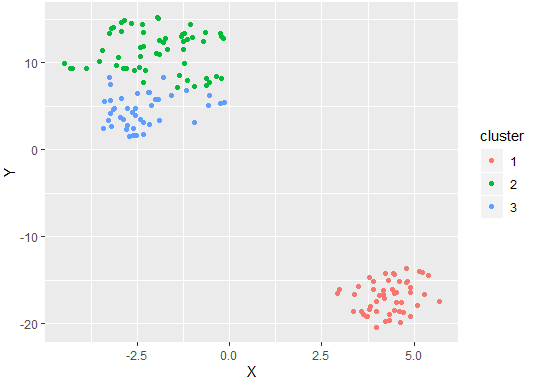
We first load the Iris dataset in a given model. Next, we train a k-medoids model to find 3 distinct clusters that we know exist here. Finally we plot this clustering. This returns the output:
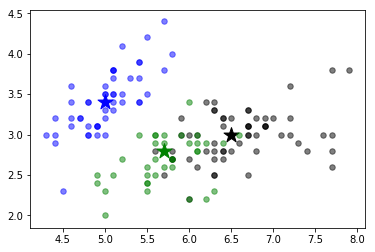
To visualize K-medoids clustering, we can use tools provided already in R, a specialized language for mathematicians, scientists, and statisticians.
library(cluster)
library(Rtsne)
library(ggplot2)
data(iris)
gower_dist = daisy(iris[,-5],metric="gower")
summary(gower_dist)
gower_mat = as.matrix(gower_dist)
sil_width = c(NA)
for(i in 2:10)
{
pam_fit = pam(gower_dist, diss = TRUE, k=i)
sil_width[i] = pam_fit$silinfo$avg.width
}
plot(1:10,sil_width,xlab="Number of Clusters",ylab="Silhouette width")
lines(1:10, sil_width)
pam_fit = pam(gower_dist, diss=TRUE, k=3)
iris$cluster = pam_fit$clustering
tsne_obj = Rtsne(gower_dist,is_distance = TRUE)
iris_plot = data.frame(tsne_obj$Y)
names(iris_plot) = c("X","Y")
iris_plot$cluster = as.factor(iris$cluster)
ggplot(aes(x=X, y=Y), data=iris_plot) + geom_point(aes(color=cluster))
Difference between PAM, CLARA, CLARANS
PAM
- As compared to the k-means algorithm, it effectively dealt with the noise and outliers present in data; because it uses medoid for the partitioning of objects into clusters rather than centroid as in k-means.
- As it performs clustering on overall data rather than only on selected samples from the data set. Hence, it does not work efficiently for large data sets.
- PAM is computable costly as it performs clustering on the overall data set.
- Its time complexity for each iteration is
O(k*(n-k)^2); where n is the number of objects in data, k is number of clusters.
CLARA
- In CLARA, it first select samples of the data from the data set, applies PAM on those samples and then outputs the best clustering out of these samples.
- Since it applies clustering by selecting samples from data so it dealt with larger data sets.
- As the sample size increases its effectiveness increases or vice-versa.
- Let suppose it draws multiple samples of smaller size and gives good clustering on it. If the selected samples are biased, it will not represent a good clustering of the overall data.
CLARANS
- At each step, it selects a sample of neighbors to examine. So it not restricts the search to a particular area. It gives the result based on the overall data.
- Now, since it examines neighbors at each step. So it is time consuming when clusters and objects are large in number.
- In CLARANS, there is a parameter for the number of local optimums. As if the local optimum is found, it again starts by randomly picking up a node to find a new local optimum. To finite this procedure, the above parameter is specified at starting.
- Since, its time complexity is
O(n^2). Hence, it is the most efficient algorithm among other k-medoids algorithms; returns higher quality clusters.
Advantages of K-medoids Algorithms
- As compared to other Partitioning algorithms, it effectively dealt with the noise and outliers present in data; because it uses medoid for the partitioning of objects into clusters.
- Easily Implementable and simple to understand.
- K-Medoid Algorithm is comparably fast as compared to other partitional algorithms.
- It outputs the final clusters of objects in a fixed number of iterations.
Disadvantages of K-medoids Algorithms
- It may results in different clusters for different runs on the same dataset because initially, we choose k medoids randomly from total objects of data and assigns them to each cluster one by one so that it becomes initial medoid of that cluster.
- It fixed the value of k(number of clusters/groups) in starting, so we don't know at what value of k the result is accurate and distinguishable.
- Its overall computational time and final distribution of objects in clusters or groups depend upon initial partition.
- Since here we distribute objects in clusters based on their minimum distance from medoid instead of centroid as in k-means. Therefore, it is not useful for clustering data in arbitrary shaped clusters.