In this article, we discuss the first phase in compiler designing where the high level input program is converted into a sequence of tokens. This phase is known as Lexical Analysis in Compiler Design.

Table of contents:

1. Definitions for Lexical Analysis
2. An example of Lexical Analysis
3. Architecture of lexical analyzer
4. Regular Expressions
5. Finite Automata
6. Relationship between regular expressions and finite automata
7. Longest Match Rule
8. Lexical errors
9. Error recovery schemes
10. Need for lexical analyzers
11. Need for lexical analyzers

Definitions for Lexical Analysis

Lexical analysis is the process of converting a sequence of characters from a source program which is taken as input to a sequence of tokens.

A lex is a program that generates lexical analyzers.

A lexical analyzer/lexer/scanner is a program which performs lexical analysis.

The roles of lexical analyzer entail;

• Reading of input characters from source program.
• Correlation of error messages with the source program.
• Striping white spaces and comments from the source program.
• Expansion macros if found in the source program.
• Entering identified tokens to symbol table.

Lexeme is an instance of a token, that is, a sequence of characters included in the source program according to the matching pattern of a token.

An example, Given the expression;
c = a + b * 5

The lexemes and tokens are;

Lexemes	Tokens
c	identifier
=	assignment symbol
a	identifier
+	+(addition symbol)
b	identifier
*	$*$(multiplication symbol)
5	5(number)

The sequence of tokens produced by the lexical analyzer enables the parser to analyze the syntax of a programming language.

A token is a valid sequence of characters given by a lexeme, it is treated as a unit in the grammar of the programming language.
In a programming language this may include;

• Keywords
• Operators
• Punctuation symbols
• Constants
• Identifiers
• Numbers

A pattern is a rule matched by a sequence of characters(lexemes) used by the token. It can be defined by regular expressions or grammar rules.

An example of Lexical Analysis

Code

#include<iostream>
// example
int main(){
    int a, b;
    a = 7;
    return 0;
}

Tokens

Lexemes	Tokens
int	keyword
main	keyword
(	operator
)	operator
{	operator
int	keyword
a	identifier
,	operator
b	identifier
;	operator
a	identifier
=	assignment symbol
10	10(number)
;	operator
return	keyword
0	0(number)
;	operator
}	operator

Non Tokens

Type	Tokens
preprocessor directive	#include<iostream>
comment	// example

The process of lexical analysis constitutes of two stages.

1. Scanning - This involves reading of input charactersand removal of white spaces and comments.
2. Tokenization - This is the production of tokens as output.

Architecture of lexical analyzer

The main task of the lexical analyzer is to scan the entire source program and identify tokens one by one.
Scanners are implemented to produce tokens when requested by the parser.

Steps:

1. "get next token" is sent from the parser to the lexical analyzer.
2. The lexical analyzer scans the input until the "next token" is located.
3. The token is returned to the parser.

Regular Expressions

We use regular expressions to express finite languages by defining patterns for a finite set of symbols.

Grammar defined by regular expressions is known as regular grammar and the language defined by regular grammar is known as regular language.
There are algebraic rules obeyed by regular expressions used to manipulate regular expressions into equivalent forms.

Operations.

Union of two languages A and B is written as
A U B = {s | s is in A or s is in B}
Concatenation of two languages A and B is written as
AB = {ss | s is in A and s is in B}
The kleen closure of a language A is written as
A* = which is zero or more occurrences of language A.

Notations.

If x and y are regular expressions denoting languages A(x) and B(y) then;
(x) is a regular expression denoting A(x).
Union (x)|(y) is a regular expression denoting A(x) B(y).
Concatenation (x)(y) is a regular expression denting A(x)B(y).
Kleen closure (x)* is a regular expression denoting (A(x))*

Precedence and associativity.

${*}_{\text{'}}$ concatenation ${.}_{\text{'}}$ and | (pipe) are left associative.
Kleen closure * has the highest precedence.
Concatenation (.) follows in precedence.
(pipe) | has the lowest precedence.

Representing valid tokens of a language in regular expressions.

X is a regular expression, therefore;

• x* represents zero or more occurrence of x.
• x+ represents one or more occurrence of x, ie{x, xx, xxx}
• x? represents at most one occurence of x ie {x}
• [a-z] represent all lower-case alphabets in the english language.
• [A-Z] represent all upper-case alphabets in the english language.
• [0-9] represent all natural numbers.

Representing occurrence of symbols using regular expressions
Letter = [a-z] or [A-Z]
Digit = [0-9] or |0|1|2|3|4|5|6|7|8|9
Sign = [+|-]

Representing language tokens using regular expressions.
Decimal = (sign)?(digit)+
Identifier = (letter)(letter | digit)*

Finite Automata

This is the combination of five tuples (Q, Σ, q0, qf, δ) focusing on states and transitions through input symbols.
It recognizes patterns by taking the string of symbol as input and changes its state accordingly.
The mathematical model for finite automata consists of;

• Finite set of states(Q)
• Finite set of input symbols(Σ)
• One start state(q0)
• Set of final states(qf)
• Transition function(δ)

Finite automata is used in lexical analysis to produce tokens in the form of identifiers, keywords and constants from the input program.

Finite automata feeds the regular expression string and the state is changed for each literal.

If the input is processed successfully, the automata reaches the final state and is accepted otherwise it is rejected.

Construction of Finite Automata

Let L(r) be a regular language by some finite automata F(A).

Therefore;

• States: Circles will represent the states of FA and their names are written inside the circles.
• Start state: This is the state at which the automata starts. It will have an arrow pointing towards it.
• Intermediate states: These have two arrows, one pointing to it and another pointing out from the intermediate states.
• Final State: Automata are expected to be in the final state when the input string has been parsed successfully and represented by double circles otherwise the input is rejected. It may contain an odd number of arrows pointing toward it and an even number pointing out from it, that is,
  odd arrows = even arrows + 1.
• Transition: When a desired symbol is found in the input, transition from one state to another state will happen. The automata either moves to the next state or persists.
  A directed arrow will display the movement from one state to another while an arrow points towards the destination state.
  If the automata stays on the same state, an arrow pointing from a state to itself is drawn.

An example; Assume that a 3 digit binary value ending in 1 is accepted by FA.
Then FA = {Q(q0, qf), Σ(0,1), q0, qf, δ}

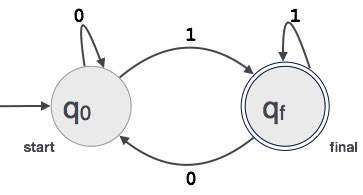
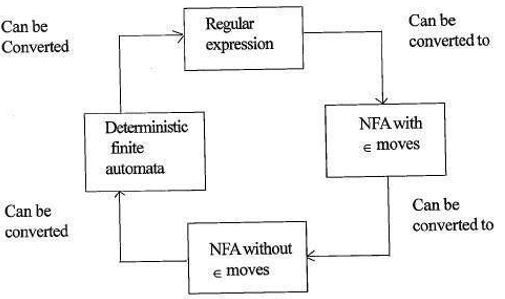
Relationship between regular expressions and finite automata

The relationship between regular expression and finite automata is as follows;
The figure below show that it is easy to convert;

• Regular expressions to Non-deterministic finite automata(NFA) with ∈ moves.
• Non-deterministic finite automata with ∈ moves to without ∈ moves
• Non-deterministic finite automata without ∈ moves to Deterministic Finite Automata(DFA).
• Deterministic Finite Automata to Regular expression.

A Lex will accept regular expressions as input, and return a program that simulates a finite automaton to recognize the regular expressions.
Therefore, lex will combine string pattern generation (regular expressions defining the strings of interest to lex) and string pattern recognition (a finite automaton that recognizes the strings of interest).

Longest Match Rule

It states that the lexeme scanned should be determined based on the longest match among all available tokens.
This is used to resolve ambiguities when deciding the next token in the input stream.
During analysis of source code, the lexical analyzer will scan code letter by letter and when an operator, special symbol or whitespace is detected it decides whether a word is complete.

Example:

int intvalue;

While scanning the above, the analyzer cannot determine whether 'int' is a keyword int or the prefix of the identifier intvalue.
Rule priority is applied whereby a keyword will be given priority over user input, which means in the above example the analyzer will generate an error.

Lexical errors

A lexical error occurs when a character sequence cannot be scanned into a valid token.
These errors can be caused by a misspelling of identifiers, keywords or operators.
Generally although very uncommon lexical errors are caused by illegal characters in a token.

Errors can be;

• Spelling error.
• Transposition of two characters.
• Illegal characters.
• Exceeding length of identifier or numeric constants.
• Replacement of a character with an incorrect character
• Removal of a character that should be present.

Error recovery entails;

• Removing one character from the remaining input
• Transposing two adjacent characters
• Deleting one character from the remaining input
• Inserting missing character into the remaining input
• Replacing a character by another character.
• Ignoring successive characters until a legal token is formed(panic mode recovery).

Error recovery schemes

Panic mode recovery.
In this error recovery scheme unmatched patterns are deleted from the remaining input until the lexical analyzer can find a well-formed token at the beginning of the remaining input.
Easier implementation is an advantage for this approach.
It has the limitation that a large amount of input is skipped without checking for any additional errors.

Local Correction.
When an error is detected at a point insertion/deletion and/or replacement operations are executed until a well formed text is achieved.
The analyzer is restarted with the resultant new text as input.

Global correction.
It is an enhanced panic mode recovery preferred when local correction fails.
It has high time and space requirements therefore it is not implemented practically.

Need for lexical analyzers

1. Improved compiler efficiency - specialized buffering techniques for reading characters speed up the compiler's process.
2. Simplicity of compiler design - The removal of white spaces and comments will enable efficient syntactic constructs for the syntax analyzer.
3. Compiler portability - only the scanner communicates with the external world.
4. Specialization - specialized techniques can be used to improve the lexical analysis process

Issues with lexical analysis

1. Lookahead
   Given an input string, characters are read from left to right one by one.
   To determine whether a token is finished or not we have to look at the next character.
   Example: Is '=' an assignment operator or the first character in '==' operator.
   Lookahead skips characters in the input until a well-formed token is found, this goes to show that look ahead cannot catch significant errors except for simple errors such as illegal symbols.
2. Ambiguities
   The programs written with lex will accept ambigous specifications an therefore choose the longest match and when multiple expressions match the input either the longest match is preferred or the first rule among the matching rules is prioritized.
3. Reserved Keywords
   Certain languages have reserved words which are not reserved in other programming languages, eg elif is a reserved word in python but not in C.
4. Context Dependency
   Example:
   Given the statement DO 10 l = 10.86, DO10l is an identifier and DO is not a keyword.
   And given the statement DO 10 l = 10, 86, DO is a keyword
   Such statements would require substantial look ahead for resolution.

Applications

1. Used by compilers create complied binary executables from parsed code.
2. Used by web browsers to format and display a web page which is parsed HTML, CSS and java script.

With this article at OpenGenus, you must have a strong idea of Lexical Analysis in Compiler Design.