Reading time: 20 minutes

Minkowski distance is a distance/ similarity measurement between two points in the normed vector space (N dimensional real space) and is a generalization of the Euclidean distance and the Manhattan distance.

Table of contents:

1. Minkowski distance in N-D space
2. Euclidean distance from Minkowski distance
3. Manhattan distance from Minkowski distance
4. Visualize Minkowshi distance
5. Applications of Minkowshi Distance

Minkowski distance in N-D space

In a N dimensional space, a point is represented as (x1, x2, ..., xN).

Consider two points P1 and P2:

P1: (X1, X2, ..., XN)
P2: (Y1, Y2, ..., YN)

Then, the Minkowski distance between P1 and P2 is given as:

$$ \sqrt[p]{{(x1-y1)}^p\ +\ {(x2-y2)}^p\ +\ ...\ +\ {(xN-yN)}^p}
$$

Note: The value of P in Minkowski Distance is set based on experimentation. The usual value of P is either 2, 3 or 4 for most problems. The exact value depends on the applications. Having the optimal value of P is critical to acheive the correct results based on the objective of the application.

The steps/ algorithm to calculate Minkowshi Distance are as follows:

1. Define the two points P1 and P2. Let there be N dimensions and set P to a specific value.
2. For each dimension DI, do the following:
   2.1 value = (P1[DI] - P2[DI])^P [Difference between the DI dimension value raised to power of P]
3. Minkowshi distance = value ^ (1/P)

Example:
Consider two points in a 7 dimensional space:
P1: (10, 2, 4, -1, 0, 9, 1)
P2: (14, 7, 11, 5, 2, 2, 18)

For a data point of view, 7 dimensions mean 7 attributes of the data in consideration which are important for the problem at hand.

The computation of Minkowski distance between P1 and P2 are as follows:

distance_pow2 = (10-14)^p + (2-7)^p + (4-11)^p + (-1-5)^p + 
                (0-2)^p + (9-2)^p + (1-18)^p

distance_pow2 = (-4)^p + (-5)^p + (-7)^p + (-6)^p + 
                (-2)^p + (7)^p + (-17)^p

minkowski_distance = distance_pow2^(1/p)

If we set p = 4 for this sample calculation, we find the following:

distance_pow2 = (-4)^4 + (-5)^4 + (-7)^4 + (-6)^4 + 
                (-2)^4 + (7)^4 + (-17)^4

distance_pow2 = 4^4 + 5^4 + 7^4 + 6^4 + 2^4 + 7^4 + 17^4

distance_pow2 = 256 + 625 + 2401 + 1296 + 16 + 2401 + 83521

distance_pow2 = 90516

minkowski_distance = distance_pow2 ^ 0.25
minkowski_distance = 90516 ^ 0.25
minkowski_distance = 17.3452

Euclidean distance from Minkowski distance

When p = 2, Minkowshi distance is same as Euclidean distance.

Then, the Euclidean distance between P1 and P2 is given as:

$$ \sqrt[2]{{(x1-y1)}^2\ +\ {(x2-y2)}^2\ +\ ...\ +\ {(xN-yN)}^2}
$$

Note: The only difference is that p = 2. Hence, Minkowski distance is a generalization of Euclidean distance. In other words, Euclidean distance is a special case of Minkowski distance.

Let us consider the same example for Euclidean distance:
Two points in a 7 dimensional space:
P1: (10, 2, 4, -1, 0, 9, 1)
P2: (14, 7, 11, 5, 2, 2, 18)

distance_pow2 = (-4)^2 + (-5)^2 + (-7)^2 + (-6)^2 + 
                (-2)^2 + (7)^2 + (-17)^2

distance_pow2 = 16 + 25 + 49 + 36 + 4 + 49 + 289

distance_pow2 = 468

euclidean_distance = 468 ^ 0.5
euclidean_distance = 21.6333

Hence, for our example with the same points in 7 dimensional space:

• Euclidean distance = 21.6333
• Minkowshi distance = 17.3452 (with p=4)

Manhattan distance from Minkowski distance

When p = 1, Minkowshi distance is same as Manhattan distance.

Then, the Manhattan distance between P1 and P2 is given as:

$$ {{(x1-y1)}\ +\ {(x2-y2)}\ +\ ...\ +\ {(xN-yN)}}
$$

Note: The only difference is that p = 1. Hence, Minkowski distance is a generalization of Manhattan distance. In other words, Manhattan distance is a special case of Minkowski distance.

Let us consider the same example for Manhattan distance:
Two points in a 7 dimensional space:
P1: (10, 2, 4, -1, 0, 9, 1)
P2: (14, 7, 11, 5, 2, 2, 18)

distance_pow2 = (-4)^1 + (-5)^1 + (-7)^1 + (-6)^1 + 
                (-2)^1 + (7)^1 + (-17)^1

distance_pow2 = -4 + (-5) + (-7) + (-6) + (-2) + 7 + (-17)

distance_pow2 = -34

manhattan_distance = -34 ^ 1
manhattan_distance = -34

Hence, for our example with the same points in 7 dimensional space:

• Manahattan distance = -34
• Euclidean distance = 21.6333
• Minkowshi distance = 17.3452 (with p=4)

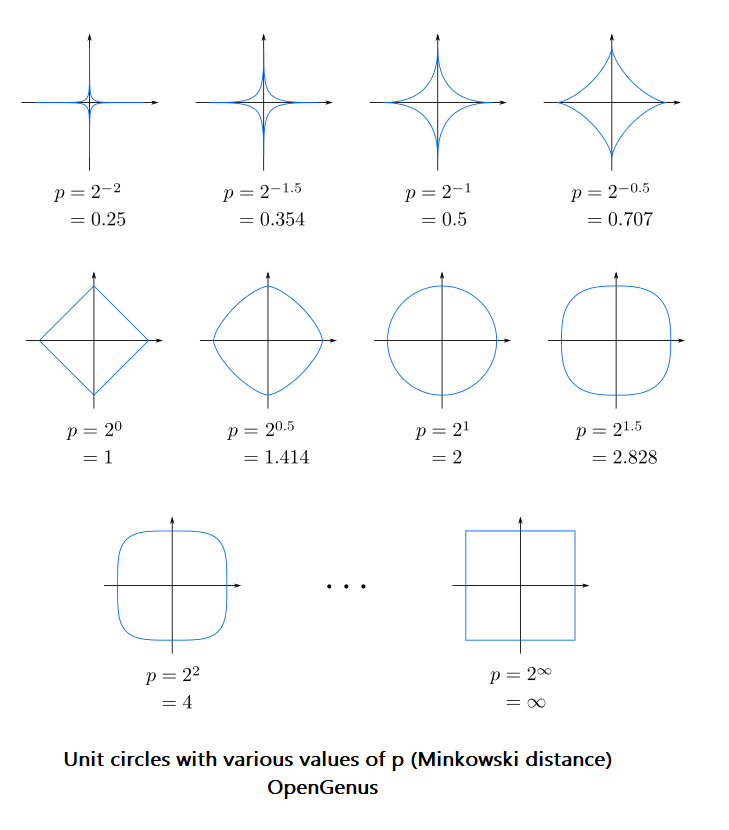
Visualize Minkowshi distance

Unit circles (path represents points with same Minkowshi distance) with various values of p (Minkowski distance):

Applications of Minkowshi Distance

Applications of Minkowshi Distance are:

• Fuzzy Clustering with Minkowski Distance Functions by Patrick J F Groenen (Erasmus University, Rotterdam), Uzay Kaymak (Eindhoven University of Technology) and Joost van Rosmalen.

• A Framework for a Minkowski Distance Based Multi Metric Quality of Service Monitoring Infrastructure for Mobile Ad Hoc Networks by Moussa Ayyash (Chicago State University).

• An Evolutionary Algorithm Based on Minkowski Distance for Many-Objective Optimization by Hang Xu, Wenhua Zeng, Xiangxiang Zeng and Gary G. Yen (IEEE members).

• "A Threshold Genetic Algorithm for Diagnosis of Diabetes using Minkowski Distance Method" by E.Sreedevi and Prof.M.Padmavathamma

Euclidean distance and Manhattan distance are same as Minkowshi Distance, hence, the applications of the previous two distance metrics are applications of Minkowshi Distance. With this article at OpenGenus, you must have the complete idea of Minkowshi Distance.