Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
In this article, we have explored Out-of-Bag Error in Random Forest with an numeric example and sample implementation to plot Out-of-Bag Error.
Table of contents:
- Introduction to Random Forest
- Out-of-Bag Error in Random Forest
- Example of Out-of-Bag Error
- Code for Out-of-Bag Error
Introduction to Random Forest
Random Forest is one of the machine learning algorithms that use bootstrap aggregation. Random Forest aggregates the result of several decision trees. Decision Trees are known to work well when they have small depth otherwise they overfit. When they are used ensemble in Random Forests, this weakness of decision trees is mitigated.
Random Forest works by taking a random sample of small subsets of the data and applies a decision tree classification to them. The prediction of the Random Forest is then a combination of the individual prediction of the decision trees either by summing or taking a majority vote or any other suitable means of combining the results.
The sampling of random subsets (with replacement) of the training data is what is referred to as bagging. The idea is that the randomness in choosing the data fed to each decision tree will reduce the variance in the predictions from the random forest model.
Out-of-Bag Error in Random Forest
The out-of-bag error is the average error for each predicted outcome calculated using predictions from the trees that do not contain that data point in their respective bootstrap sample. This way, the Random Forest model is constantly being validated while being trained. Let us consider the jth decision tree \(DT_j\) that has been fitted on a subset of the sample data. For every training observation or sample \(z_i = (x_i , y_i)\) not in the sample subset of \(DT_j\) where \(x_i\) is the set of features and \(y_i\) is the target, we use \(DT_j\) to predict the outcome \(o_i\) for \(x_i\). The error can easily be computed as \(|o_i - y_i|\).
The out-of-bag error is thus the average value of this error across all decision trees.
Example of Out-of-Bag Error
The following is a simple example of how this works in practice. Consider this toy dataset which records if it rains given the temperature and humidity:
| S/N | Temperature | Humidity | Rained? |
|---|---|---|---|
| 1 | 33 | High | No |
| 2 | 18 | Low | No |
| 3 | 27 | Low | Yes |
| 4 | 20 | High | Yes |
| 5 | 21 | Low | No |
| 6 | 29 | Low | Yes |
| 7 | 19 | High | Yes |
Assume that a random forest ensemble consisting of 5 decision trees \(DT_1 ... DT_5\) is to be trained on the the dataset. Each tree will be trained on a random subset of the dataset. Assuming for \(DT_1\) that the randomly selected subset contains the first five samples of the dataset. Therefore, the last two samples 6 and 7 will be the out-of-bag samples on which \(DT_1\) will be validated. Continuing with the assumption, let the following table represent the prediction of each decision tree on each of its out-of-bag samples:
| Tree | Sample S/N | Prediction | Actual | Error (abs) |
|---|---|---|---|---|
| DT1 | 6 | No | Yes | 1 |
| DT1 | 7 | No | Yes | 1 |
| DT2 | 2 | No | No | 0 |
| DT3 | 1 | No | No | 0 |
| DT3 | 2 | Yes | No | 1 |
| DT3 | 4 | Yes | Yes | 0 |
| DT4 | 2 | Yes | No | 1 |
| DT4 | 7 | Yes | Yes | 1 |
| DT5 | 3 | Yes | Yes | 0 |
| DT5 | 5 | No | No | 0 |
From the above, the out-of-bag error is the average error which is 0.5.
We thus see that because only a subset of the decision trees in the ensemble is used in determining each error that is used to compute the out-of-bag score, it cannot be considered as accurate as a validation score on validation data. However, in cases such as this where the dataset is quite small and it is impossible to set aside a validation set, the out-of-bag error can prove to be a useful metric.
Code for Out-of-Bag Error
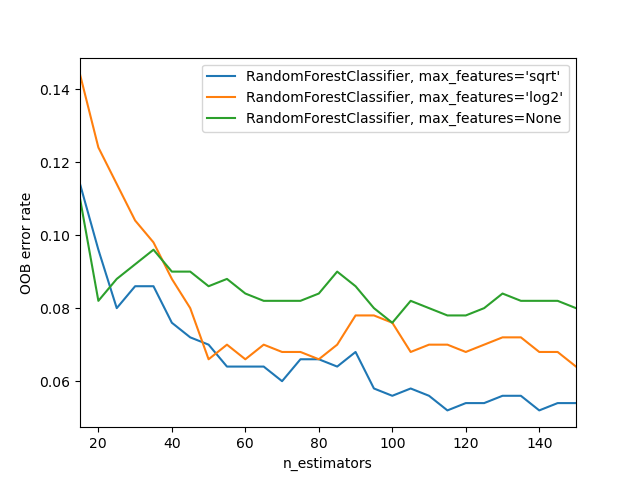
Lastly, we demonstrate the use of out-of-bag error in the estimation of a suitable value for the choice of n_estimators for a random forest model in scikit-learn library. This example is adapted from the documentation. The out-of-bag error is measured at the addition of each new tree during training. The resulting plot shows that the choice of 115 for n_estimators is optimal for the classifier (with 'sqrt' max_features) in this example.
import matplotlib.pyplot as plt
from collections import OrderedDict
from sklearn.datasets import make_classification
from sklearn.ensemble import RandomForestClassifier
RANDOM_STATE = 123
# Generate a binary classification dataset.
X, y = make_classification(
n_samples=500,
n_features=25,
n_clusters_per_class=1,
n_informative=15,
random_state=RANDOM_STATE,
)
# NOTE: Setting the `warm_start` construction parameter to `True` disables
# support for parallelized ensembles but is necessary for tracking the OOB
# error trajectory during training.
ensemble_clfs = [
(
"RandomForestClassifier, max_features='sqrt'",
RandomForestClassifier(
warm_start=True,
oob_score=True,
max_features="sqrt",
random_state=RANDOM_STATE,
),
),
(
"RandomForestClassifier, max_features='log2'",
RandomForestClassifier(
warm_start=True,
max_features="log2",
oob_score=True,
random_state=RANDOM_STATE,
),
),
(
"RandomForestClassifier, max_features=None",
RandomForestClassifier(
warm_start=True,
max_features=None,
oob_score=True,
random_state=RANDOM_STATE,
),
),
]
# Map a classifier name to a list of (<n_estimators>, <error rate>) pairs.
error_rate = OrderedDict((label, []) for label, _ in ensemble_clfs)
# Range of `n_estimators` values to explore.
min_estimators = 15
max_estimators = 150
for label, clf in ensemble_clfs:
for i in range(min_estimators, max_estimators + 1, 5):
clf.set_params(n_estimators=i)
clf.fit(X, y)
# Record the OOB error for each `n_estimators=i` setting.
oob_error = 1 - clf.oob_score_
error_rate[label].append((i, oob_error))
# Generate the "OOB error rate" vs. "n_estimators" plot.
for label, clf_err in error_rate.items():
xs, ys = zip(*clf_err)
plt.plot(xs, ys, label=label)
plt.xlim(min_estimators, max_estimators)
plt.xlabel("n_estimators")
plt.ylabel("OOB error rate")
plt.legend(loc="upper right")
plt.show()