Rabin-Karp Pattern Searching Algorithm

The problem is to find a pattern P in a given string S. This is a very common problem and various solutions are there to tackle this. In this article we are going to discuss the Rabin-Karp Algorithm.

Rabin-Karp Algorithm is a wonderful algorithm that utilizes the technique of hashing to search for patterns in a string in linear time by using a clever way of calculating hashes. This algorithm has been developed by Richard M. Karp and Michael O. Rabin in 1987. We develop the basic ideas behind the algorithm and delve into the practical use of this algorithm as well.

The obvious naive approach in this problem is this to check the pattern P at every index of string S till we get a mismatch or pattern is found at the index. Then we can just output all the indices where we found the pattern in the string. But the time complexity of this approach is O(|P|*|S|) where |P| is length of the pattern and |S| is length of the string. This approach is not feasible for most practical purposes.

Now to improve our time complexity we will use Rabin-Karp Algorithm.

This algortihm uses hashes to determine whether we need to check the whole pattern or not. If you don't know what hashes are then, hashes are mappings of arbitrary size data to a fixed size data. In simple words, we can represent our data with a specific value determined by a function (refer to the image below). The function which is used to get values is called a Hash Function and the values are called hashes.

As you can see in the image, whole string can be mapped to something as simple as an integer value. Using this we can compare whole strings at one go by comparing just their hashes and not every single character. Before we move further let us see how exactly we are going to hash strings.

Comparing two strings of length N takes O(N) time complexity but comparing two integers takes O(1) time complexity

For proper hashing, the hashing function used should have least collisions possible.

What is collision? When two distinct keys are hashed or mapped to same value then it is called a collision. To convert a string into a hash we treat every character as an distinct integer like ASCII or Unicode. Now, we hash our string like a polynomial function. In polynomial function there is a variable x on which value of function depends.

We select this x randomly and make a polynomial function of degree equal to |S|-1. So, the coefficients of various powers of x are the integer value of the corresponding character.

This is how strings are hashed but there is a problem. If our randomly selected value is large or our string is long then the integer value will be very large. To avoid this problem we take mod of the hash value with an integer p. The integer p is a prime number because a prime number has no factors other than 1 and itself so, the number of collisions will be least. We take this prime number as large as possible.

Pattern Searching using Hashes

It is clear now that the way we have implemented our hash function it is very rare that two distinct string will have same hash value. It is guaranteed that if hash value of two string are different given that are of equal length then the strings are distinct. So, if we have hash value of pattern and hash values for all sub-strings of given string of length equal to that of pattern we will check only the sub-strings which have hash value equal to that of pattern. This way we can avoid several string comparisons just by comparing their hashes.

Now the problem that remains is to efficiently compute hashes for all sub-string of length equal to that of pattern. For this we need to observe that hashes of two consecutive strings is very similar (not equal).

Take a look at this example carefully:

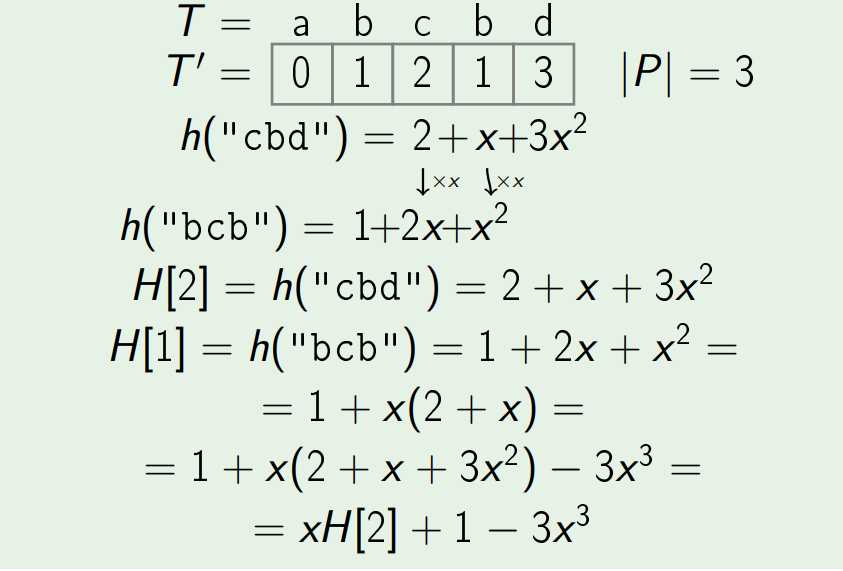
Now, on close observation we can see it is an recurrence relation. If we solve this relation the result is:

H[i] = ( x*H[i+1] + S[i] - S[i + |P|] * x ^|P| ) mod p

or,

H[i+1] = ( x*H[i] + S[i+1] - S[i - |P|] * x ^|P| ) mod p

Where,
H is an array of hash value containing hashes of all sub-strings.
p is a big prime number
x is random integer between 1 and p-1
|P| is length of the pattern
S is given string in which pattern is to be searched

In this way, we can get hash value of all sub-strings in single scan of the string that is in O(N) time complexity.

After we get all the hash values we will just compare sub-strings whose hash values are equal to that of the pattern. There is one more thing to note: we can choose any one of the two recurrence relation but the algorithm for both of them is also different. If first relation is used we will compute hashes from the end of the string to the begining and in the second relation hashes will be computed from the beginning to the end of the string.

Space Complexity: O(|P| + |S|)
Time Complexity (average and best): O(|P| + |S|)
Time Complexity (worst): O(|P| X |S|)

Worst case complexity occurs when all the hashes of sub-strings and pattern are equal.

C++ implementation of Rabin-Karp is given below:

#include <iostream>
#define MOD 1000000007 // selected prime number
using namespace std;

int main(){
    string pattern, text;
    cin >>pattern >>text;

    int l1 = pattern.length(), l2 = text.length();
    long long hp = 0, ht = 0, val = 1;

    srand(time(0));
    long long random = rand()%(MOD-1) + 1; // generating random value x

    for(int i=0; i<l1 ;i++){
        hp = (random*hp)%MOD; // calculating hash of pattern
        ht = (random*ht)%MOD; // calculating hash of first sub-string
                              // of text
        hp += pattern[i];
        ht += text[i];

        hp %= MOD;
        ht %= MOD;
        val = (val*random)%MOD;
    }
    
    for(int i = 0; l2-l1-i >= 0 ;i++){
        if(i != 0){
            long long new_ht = (random*ht-val*text[i-1]+text[l1+i-1])%MOD;
            new_ht = (new_ht + MOD)%MOD;
            ht = new_ht;
        }

        if(hp == ht){
            int j;
            
            for (j = 0; j < l1 ; j++){ 
                if (text[i+j] != pattern[j]) 
                    break; 
            }
            
            if(j == l1)
               cout <<i <<" "; //output all indices where pattern was
                               //found in text
        }
    }

    return 0;
}

• The Rabin–Karp algorithm is inferior for single pattern searching to Knuth–Morris–Pratt algorithm, Boyer–Moore string search algorithm and other faster single pattern string searching algorithms because of its slow worst case behavior.

• It is the preferred algorithm for multiple pattern search.

• A practical application of the algorithm is detecting plagiarism. Given source material, the algorithm can rapidly search through a paper for instances of sentences from the source material, ignoring details such as case and punctuation. Because of the abundance of the sought strings, single-string searching algorithms are impractical.

• Rabin-Karp performs worse in cases when most of the hashes are equal but otherwise it is a good pattern searching algorithm. Some of the worst cases can be checked beforehand to avoid worst time complexity. Other than that, if we are sure that no such cases are there in our problem then we can use this algortihm and expect a decent running time. Rabin-Karp can be used for exact pattern matching and in cases where our pattern and text have different characters in them with no possibility of *consecutive repitition of a character.