
Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
Reading time: 35 minutes | Coding time: 10 minutes
In the range minimum query problem, we have to optimize two queries. One query is to find minimum value in a given range and the other query is to update an element at a given index. The update operation changes the minimum element in involved ranges which makes this a difficult problem.
In this article, we have solved this problem using Segment Tree and this takes O(log N) time for both update and range query.
Problem Statement
Compute the minimum element in the given array within index ranges given by the user.
In this article we are going to explain the algorithms to solve range minimum queries .
We are given an array A[0....N-1].
The problem consist of two parts-:
-
Update(i,val): In this part we have to update an element at index i with val
-
Query(l,r): In this part we have to return the minimum value between index ‘l’ and ‘r’ inclusive
Example
Given an array A[] = {1,4,3,5,6,7}.
Tasks-:
- Compute the minimum element in the range (l,r)=(2,5).
- Update the value at index 3 to '0'.
- Compute the minimum element in the range (l,r)=(2,5).
Answers-:
- Minimum element in the index range (2,5) is '3'
- Minimum element in the index range (2,5) after updating element at index 3 is '0'
Segment Tree
Basic Idea: The root of the tree will represent the whole array A[0:N-1]
Then it is broken into segments and first child will represent A[0:(N-1)/2]
and second will represent A[(N-1)/2+1:(N-1)] and so on each segment is divided. This makes the height of the segment tree to be log(n).
Total number of nodes= n + (n-1) = 2n-1 Now, we know its a full binary tree and thus the height is: ceil(Log2(n)) +1
Total no. of nodes = 2^0 + 2^1 + 2^2 + … + 2^ceil(Log2(n)) // which is a geometric progression where 2^i denotes, the number of nodes at level i.
Formula of summation G.P. = a * (r^size - 1)/(r-1) where a=2^0
Total no. of nodes =1(2^(ceil(Log2(n))+1) -1)/(2-1)*
= 2 [2^ceil(Log2(n))] -1* (you need space in the array for each of the internal as well as leaf nodes which are this count in number), thus it is the array of size.
= O(4 * n) approx..
We will be implementing the segment tree approach using three functions namely-
-
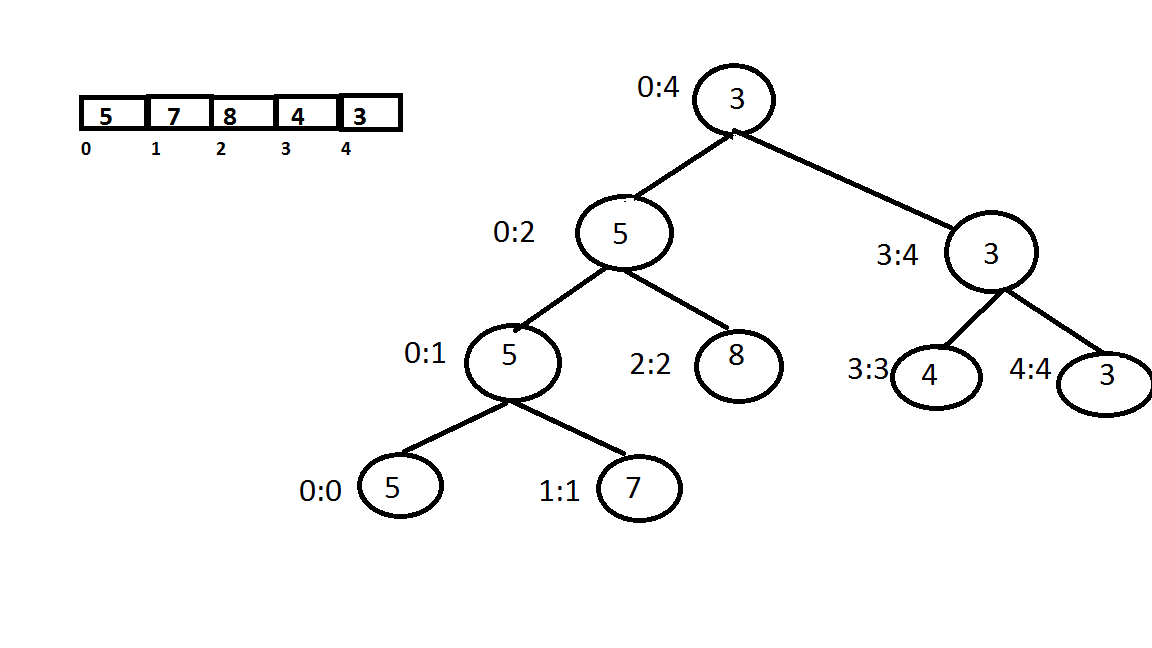
Build()- In this function we divide the array into segments with the particular node representing the minimum element in the segment represented by it. We need to recurse to the bottom each time after finding the middle of the segment and store the leaf nodes in the 'tree' array, then store the minimum in the corresponding nodes using bottom up approach.
-
Query()- This function is implemented in three steps-
-
1 If the given range completely overlaps with the segment then return the value of the node.
-
2 If the given range partially overlaps with the segment then recurse through the left and right subtree.
-
3 If the given range does not overlap with the segment then return INT_MAX or the maximum integer value.
-
Update()- In this function we search the leaf mode that contains the element to be updated. This can be done by going to either on the left child or the right child depending on the interval which contains the element.Once the leaf is found update it with the given element and recurse again from the bottom using the bottom up approach and update all the nodes that come in the path uptil the root node.
A detailed working explanation can be understood through the Psuedo Code.
Time Complexity
Build-Building a segment tree takes O(n) time complexity as we have to traverse through the whole array.
Pseudocode of build():
//node represents the root
//start represents the starting index
//end represents the last index
Build(node,start,end)
{
if(start == end)
// Leaf node will have a single element
tree[node] = A[start];
else
int mid = (start + end) / 2;
// Recurse on the left child
build(2*node, start, mid);
// Recurse on the right child
build(2*node+1, mid+1, end);
// Internal node will hold the minimum of two children
tree[node] = min(tree[2*node],tree[2*node+1]);
}
Query-Recurse on the segment tree from the root and find whether the interval is a total overlap,partial overlap or no overlap with the given interval (will be discussed in later section) so each query takes O(log(n)) time to be processed as in the worst case the whole tree would be recursed.
To query on a segment tree we should check three condtitions-:
- Range represented by the node is completely inside the given range.
- Range represented by a node is completely outside the given range.
- Range represented by a node is partially inside and partially outside the given range
query(node, start, end, l, r)
{
if(r < start or end < l)
{
// Case 1
// range represented by a node is completely outside the range
// return the maximum value
return INT_MAX;
}
if(l <= start and end <= r)
{
// Case 2
// range represented by a node is completely inside the given range
// return the node value itself
return tree[node];
}
// Case 3
// range represented by a node is partially inside and partially outside the given range
// recurse through the left and right subtree according to the above specified conditions
int mid = (start + end) / 2;
int q1 = query(2*node, start, mid, l, r);
int q2 = query(2*node+1, mid+1, end, l, r);
return min(q1,q2)
}
Update-Search the leaf that contains the element to update. This can be done by going to either on the left child or the right child depending on the interval which contains the element.Once the leaf is found update it with the given element and recurse again from the bottom using the bottom up approach and update all the nodes that come in the path uptil the root node.The complexity for update operation is also O(log(n)) .
Pseudocode of update():
//idx represents the index at which the value is to be changed
//val represents the new value
Update( node, start, end, idx, val)
{
if(start == end)
// Leaf node updated with 'val'
A[idx]=val;
tree[node]=val;
else
int mid = (start + end) / 2;
if(start <= idx and idx <= mid)
// If idx is in the left child, recurse on the left child
update(2*node, start, mid, idx, val);
else
// if idx is in the right child, recurse on the right child
update(2*node+1, mid+1, end, idx, val);
// Internal node will hold the minimum of two children
tree[node] = min(tree[2*node],tree[2*node+1]);
}
C++ implementation-:
Following is the complete C++ implementation to solve Range Minimum query problem using Segment Tree:
#include <bits/stdc++.h>
using namespace std;
void build(int node,int start,int end,int tree[],int a[])
{
if(start==end)
{
tree[node]=a[start];
}
else
{
int mid=(start+end)/2;
build(2*node+1,start,mid,tree,a);
build(2*node+2,mid+1,end,tree,a);
tree[node]=min(tree[2*node+1],tree[2*node+2]);
}
}
void update(int node,int start,int end,int idx,int val,int tree[],int a[])
{
if(start==end)
{
a[idx]=val;
tree[node]=val;
}
else
{
int mid=(start+end)/2;
if(idx>=start&&idx<=mid)
{
update(2*node+1,start,mid,idx,val,tree,a);
}
else
{
update(2*node+2,mid+1,end,idx,val,tree,a);
}
tree[node]=min(tree[2*node+1],tree[2*node+2]);
}
}
int query(int node,int start,int end,int l,int r,int tree[])
{
if(l>end||start>r)
{
return INT_MAX;
}
if(l<=start&&r>=end)
{
return tree[node];
}
int q1,q2;
int mid=(start+end)/2;
q1=query(2*node+1,start,mid,l,r,tree);
q2=query(2*node+2,mid+1,end,l,r,tree);
return(min(q1,q2));
}
int main()
{
int tree[15];
int a[]={4,5,3,2,4,6,6,3};
int n=sizeof(a)/sizeof(a[0]);
build(0,0,n-1,tree,a);
cout<<"query(3,6) before update :"<<query(0,0,n-1,3,6,tree)<<"\n";
update(0,0,n-1,3,0,tree,a);
cout<<"query(3,6) after update :"<<query(0,0,n-1,3,6,tree)<<"\n";
return 0;
}
Output:-
query(3,6) before update :2
query(3,6) after update :0
Different ways to solve this problem:
There are different ways to solve this problem:
-
- query in O(N)
- update in O(1)
-
- query: O(square-root of N)
- update: O(1)
-
- query: O(log N)
- update: O(log N)
-
- query: O(log N)
- update: O(N log N)
-
- query: O(1)
- update: O(N log N)
-
Cartesian Tree and Farach-Colton and Bender algorithm
- query: O(1)
- update: O(N)
With this, you should have a strong basic knowledge of this problem. We will work over improving this with other efficient approaches in our other articles. Enjoy.
